Categorie: Matematica
Tags: area triangolo geometria quiz triangolo rettangolo
Scritto da: Vincenzo Zappalà
Commenti:9
Un triangolo in difficoltà *
Facciamo divertire anche i meno esperti... Un povero triangolo rettangolo è sicuramente molto intelligente, ma ha appena iniziato lo studio della geometria e della matematica. Gli si fa una domanda che sembra irrisolvibile per la sua limitata preparazione. Riuscite ad aiutarlo?
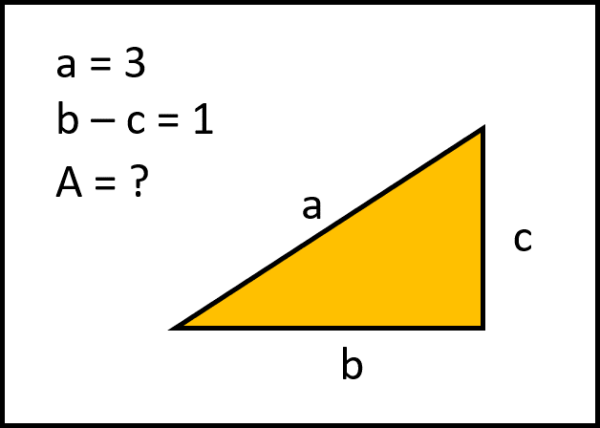
Il nostro triangolo rettangolo sa soltanto che è rettangolo, che il suo lato più lungo è uguale a 3 e che la differenza tra gli altri due lati è uguale ad 1. Gli si chiede di determinare in meno di un minuto (o giù di lì) la sua area.
Il triangolo è in grande difficoltà dato che conosce soltanto le quattro operazioni (somma, differenza, prodotto e divisione) per quanto riguarda l'aritmetica, mentre conosce solo il quadrato, il suo perimetro e la sua area, per quanto riguarda la geometria. Non sa assolutamente come si può determinare l'area di un triangolo e di un rettangolo e, ovviamente, non conosce il teorema di Pitagora e altri teoremi simili. Il cerchiò è ancora un mistero e , oltretutto, non saprebbe nemmeno usare un compasso. Insomma, è proprio alle prime armi, ma è molto intelligente.
Insomma, cercate di aiutarlo: è veramente simpatico e se lo merita!
La soluzione la trovate QUI






9 commenti
Eleviamo al quadrato (b - c) = 1 e otteniamo:
(1). b2 + c2 - 2bc = 1
Per il teorema di Pitagora è b2 + c2 = a2
Sostituendo nella (1) otteniamo:
a2 - 2bc = 1, o anche
(2). 2bc = a2 - 1.
Poiché b - c = 1 avremo anche b = c + 1 che sostituendo nella (2), questa diventa:
(3). 2(c + 1)c = a2 + 1
Eseguendo le moltiplicazioni in parentesi e sostituendo ad a il valore 3 (dato del problema), si ottiene la seguente equazione di secondo grado:
(4). c2 + c - 4 = 0
che ha due soluzioni:
c1= (-√17 - 1)/2, negativa che non ha alcun valore pratico nel nostro problema perché un segmento non può mai avere lunghezza negativa.
c2 = (√17 - 1)/2, che d'ora in poi sarà la nostra c.
Dalla (b - c) = 1 otteniamo
b = c + 1, ovvero (√17 - 1)/2 + 1. Quindi sarà:
b = (√17 + 1)/2
Come è noto l'area del nostro triangolo rettangolo è:
A = bc/2 dove sostituendo i valori di b e c trovati avremo:
A = ((√17 - 1)/2)(√17 + 1)/2))/2 = (17 - 1)/8 (per il prodotto notevole "somma di due monomi per la loro differenza"). Quindi completando i calcoli, la soluzione trovata è:
A = 2
caro Carlo,
eh no... Nell'articolo c'è scritto chiaro che il triangolo non conosce Pitagora e nemmeno l'area del triangolo. Tanto meno le equazioni di secondo grado...
Deve farne a meno...
sapendo solo calcolare l'area del quadrato, il suo perimetro e le quattro operazioni aritmetiche sarebbe stato molto più facile se il triangolo rettangolo fosse stato isoscele in quel caso avrebbe certamente dedotto che l'area del triangolo è la metà di quella del quadrato che ha il lato uguale alla misura del cateto
ma non è isoscele...
Credo che l'area sia pari a 2, come già detto nel primo commento. Avendo a disposizione solamente le quattro operazioni aritmetiche ed alcune proprietà del quadrato, si può arrivare al suddetto risultato nel seguente modo:
Spero che il procedimento sia quello giusto.
La sottrazione delle due aree deve dare 8, purtroppo il numero è stato sostituito da una faccina
Bravo Daniele! Ottima risposta
Grazie Prof. Zappalà!
Ho iniziato da pochi giorni a leggere e studiare il suo corso di matematica e ammetto che, dopo aver letto la lezione n. 5, tale quesito sia capitato proprio al momento giusto.
grazie a te Daniele! e -ricordati- che qui ci diamo tutti del TU. Continua a seguirci, mi raccomando