Uno studio di funzione piuttosto semplice... tanto per non dimenticare. Basta prendere quattro quadrati e trovare l'area di un triangolo, che la sta cercando disperatamente. Ah... questi triangoli... hanno sempre bisogno di aiuto!

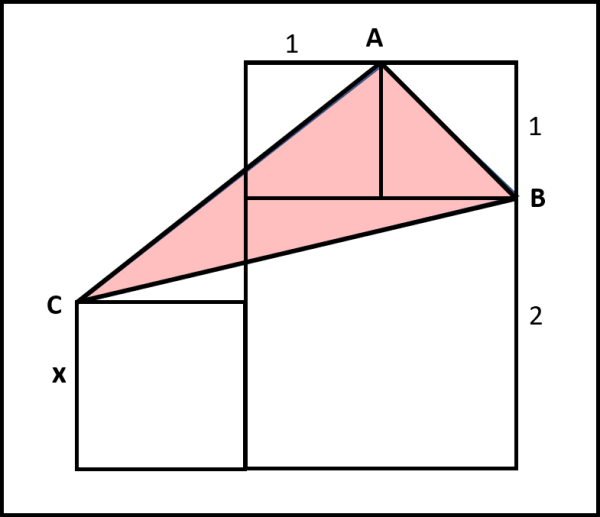
Mettiamo un bel quadrato di lato uguale a 2 e mettiamoci sopra due quadrati di lato uguale a 1. A fianco (per esempio, a sinistra), inseriamo un altro quadrato qualsiasi di lato uguale a x. A questo punto, disegnare il nostro triangolo ABC, come rappresentato in figura.

Si chiede: "Come varia l'area del triangolo ABC al variare del lato x del quadrato di sinistra?".

In pratica, si chiede l'Area y in funzione del lato x, ossia  lo studio della funzione  y = f(x). Un grafico sarebbe il benvenuto!

SOLUZIONE

Il nostro Leandro ha subito scoperto il piccolo inganno... Per comprendere meglio la soluzione basta ruotare la nostra figura in modo che la base AB del triangolo sia posta in orizzontale (Fig. 1).

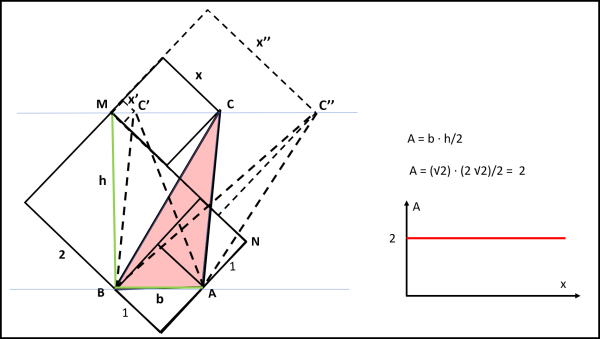
Vediamo subito che la base non è altro che la diagonale del quadrato di lato 1, ossia vale b = √2. Passiamo adesso al quadrato di lato variabile x. Essendo posizionato lungo la linea MN si nota facilmente che il suo punto C descrive una retta parallela alla base AB. Ne deriva che, qualsiasi sia il quarto quadrato di lato variabile x, l'altezza del triangolo di partenza vale sempre h che è proprio la diagonale del quadrato di lato 2, ossia h = 2√2. In poche parole, al variare di x, l'area dei triangoli ABC, ABC', ABC'' rimane sempre la stessa e vale:

A = b · h/2 = √2 · 2√2/2 = 2

La funzione A = A(x) non è altro che la retta parallela all'asse x, A = 2.

Mi sa che devo complicare un po' i quiz...