Finalmente un triangolo che conosce bene la trigonometria! ***

21/12/19

Finalmente un triangolo che conosce bene la trigonometria! ***

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:17

Dopo tanti triangoli abbastanza "imbranati", eccone uno molto preparato i cui vertici si divertono a proporsi, a vicenda, dei problemi non proprio banali. Questo è il regalino di Natale per i più esperti (ma nemmeno troppo, in fondo...).

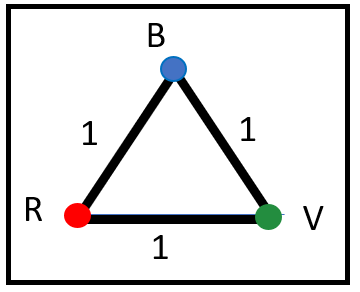
BRV è un triangolo equilatero di lato unitario.

vertici

I suoi tre vertici (B = blu, R = rosso, V = verde) sono molto irrequieti e faticano a stare fermi. Inoltre, B si considera il più esperto e R e V le studiano tutte per metterlo in difficoltà. Ecco che cosa hanno escogitato questa volta:

R inizia a muoversi sul prolungamento di BR verso il basso. Vorrebbe fare le cose più complicate, ma poi decide di non esagerare, per cui si ferma nel punto R' tale che R'R = RB = 1. Si volta e continua a camminare in linea retta verso il vertice V, lo supera e continua nel suo moto. Poi si ferma e attende... A questo punto è la volta del vertice V che si muove verso destra lungo il prolungamento di RV. Poi si ferma anche lui e comincia a confabulare con il vertice rosso. Si muovono un pochino lungo le loro traiettorie fino ad allinearsi perfettamente con B. In altre parole, R' si porta in R'' e V in V' tali che B, R'' e V' siano  allineati. Tuttavia, cercano di semplificare ancora un po' la configurazione e si sistemano in modo che R''V' sia uguale  a 1.

A questo punto chiedono al vertice blu: "Qual è la distanza  che dovresti percorrere per raggiungere R''  lungo la retta che ti collega con lui e V'?"

I vertice blu conosce bene la trigonometria, inizia a fare un po' di conti e, alla fine, dà la risposta esatta.

Forza, cercate di imitarlo!

Soluzione QUI

Articoli correlati

17 commenti

  1. michele celenza
    21/12/2019 at 16:37

    http://www.infinitoteatrodelcosmo.it/wp-content/uploads/2019/12/michele.png

    Il triangolo BRV è equilatero e quindi equiangolo il lato misura 1 ogni vertice misura 60°.

    R' sta in basso sul prolungamento del lato BR e sappiamo che RR'=1.

    Dal punto R' lo spostamento del vertice rosso è sulla linea retta passante per V ed in direzione da R' a V.

    Il triangolo R'R'V è per costruzione isoscele RR' = RV = 1, posso calcolare la base R'V con il teorema di Carnot:

    R'V = (RR')2 +  (RV)2- 2 (RV)*(RR') cos 120°   ( l'angolo R'RV è il supplementare di 60° quindi vale 120°)

    R'V = 1+1 - 2 *1*1*(-1/2) =  3.

    per costruzione sappiamo che  B, R'' e V' sono situati sulla stessa retta e R" e intermedio tra B e V'.

    Considero il triangolo BVR" il cui angolo in V è retto infatti:

    l'angolo RVR'  è di 30° in quanto il triangolo  RVR' è per costruzione isoscele sui lati RR' e RV quindi gli angoli alla base valgono 30° l'angolo in R è di 120°. L'angolo BVR" è supplementare di (60°+  30°) quindi vale 90°.

    ora prendo in  considerazione il triangolo VR"V' so per costruzione che   R"V' = 1 posso considerare tale triangolo iscritto in una circonferenza di raggio r incognito che posso calcolare con il teorema della corda:

    R"V' = 2r sin (angolo R"VV')

    l'angolo R"VV' vale 30° dovendo essere il supplementare di  (90° +60°),

    sostituendo  i dati si ha

    R"V' = 2 r sin 30° = 2 r 1/2

    1 = 2 r 1/2     r= 1

    essendo r =1  ovvero il raggio della circonferenza nella quale è inscritto il triangolo VR"V' detto O il suo centro deve essere OR"= 1 e OV' = 1   ovvero il triangolo R"OV' è equilatero ed equiangolo ma anche il triangolo R"OV è equilatero per cui VR" = 1.

    ricordando che il triangolo BVR" è retto in V e che i sui cateti sono entrambi uguali ad 1

    posso calcolare l'ipotenusa BR" ovvero la distanza che deve compiere il vertice blu per raggiungere R"

    (BR")2 = 12 + 12 = 2   BR = radice (2 ) =  1,41....

     

  2. Vincenzo Zappalà
    21/12/2019 at 17:55

    Caro Michele,

    tu dici:

    " ... ma anche il triangolo R"OV è equilatero per cui VR" = 1..."

    Perché deve essere equilatero? Non è soltanto isoscele?

  3. Michele Celenza
    21/12/2019 at 19:30

    Sì è solo isoscele in quanto si sa che dal centro del cerchio ai due estremi della corda VR'' i due raggi valgono 1 quindi gli angoli alla base sono uguali ma incogniti come pure è incognito l'angolo al vertice.

    Mi sono confuso con una sorta di "simmetria". Ora debbo ragionare per determinare il lato VR''

  4. leandro
    21/12/2019 at 22:27

    abbiamo

    \alpha =VBR"

    \beta =VR"B

    \delta = VV'R"

     

    \alpha +\beta =\frac{\pi }{2}

    perché VBR" è rettangolo

    \alpha +\delta =\frac{\pi }{2}

    perché BVV' =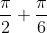 \frac{\pi }{2}+\frac{\pi }{6}

    \delta +\frac{\pi }{6} = \beta

    perché \beta è angolo esterno di VV'R"

    IL sistema seguente risolve i i tre angoli incogniti

    \begin{bmatrix} 1 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 1 \end{bmatrix}\begin{bmatrix} \alpha \\ \beta \\ \delta \end{bmatrix}= \begin{bmatrix} \frac{1 }{2}\\ \frac{2}{3}\\ \frac{1}{6} \end{bmatrix}\pi

    Infine:

    distanza BR" = \frac{1}{\sin \beta }

    perché , ricordiamo, VBR" è rettangolo

  5. Vincenzo Zappalà
    22/12/2019 at 07:23

    caro Leandro,

    sappiamo benissimo che tu sei molto bravo. Tuttavia, io inserisco molti quiz per stimolare l'interesse e far partecipare persone di tutti i livelli (o quasi). Come avrai visto, nelle mie soluzioni non lascio indietro nessun passaggio, a costo di essere noioso e pedante, ma lo scopo è proprio quello di spiegare a tanti e non a pochi intimi. Le risposte dei più bravi dovrebbero seguire questa strategia: questo è lo spirito del Circolo.

    Ti pregherei, perciò, di esprimere il tuo sistema in modo più chiaro a tutti (le matrici e i determinanti li abbiamo appena sfiorati) e indicare il risultato numerico, dato che tale deve essere.

    Grazie!

  6. Vincenzo Zappalà
    22/12/2019 at 07:55

    Inoltre, Leandro...

    tu dici che alfa + delta = 90     .... da cosa lo derivi?

    e poi temo che le tre equazioni non siano indipendenti...

  7. leandro
    22/12/2019 at 13:02

    Ok il determinante era nullo.

    Per rimediare prendo il cerchio passante per V V' e R". R"V' è una corda che insiste in V per 30° e quindi al centro O  per 60° . R"OV' è isoscele .

    Il lato=raggio è

    \frac{1}{\sqrt{2}}

    e l'angolo al centro è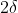 2\delta, cioè il doppio dell'angolo alla circonferenza.

    Il cateto VR" è 2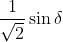 \frac{1}{\sqrt{2}} \sin \delta

    da cui,  con il vecchio Pitagora, si ottiene

    x^{2}= 2 (\sin \delta) ^{2 } +1

  8. leandro
    22/12/2019 at 13:11

    Mi direte: ma delta quanto vale? ovviamente 30°. OVR" è equilatero e quindi VR" = 1.

    x= \sqrt{2}

  9. Vincenzo Zappalà
    22/12/2019 at 15:36

    Dunque... caro Leandro, stai seguendo l'approccio di Michele e penso che tu cada nello stesso inganno.

    R''OV' non solo è isoscele, ma anche equilatero, dato che l'angolo al centro è 60. Il triangolo OVR'' invece è soltanto isoscele e non conosciamo delta... (il raggio, tra parentesi, deve valere 1 se il triangolo è equilatero...)

    Sei arrivato alla stessa conclusione di Michele...

  10. Vincenzo Zappalà
    22/12/2019 at 16:22

    Per eliminare ogni dubbio, inserisco una figura fatta con buona precisione, adottando i simboli di Leandro.

    Si vede chiaramente che le conclusioni di Leandro, simili a quelle di Michele, sono errate e si basano solo su un disegno approssimativo... Comunque la faccenda era già visibile nel disegno di Michele che è stato inserito stamattina come link...

  11. michele celenza
    23/12/2019 at 15:18

    Si dalla figura riportata da Vincenzo risulta visivamente che il triangolo VOR" e solamente isoscele.

    D'altra parte del triangolo VV'R" si conoscono solo il lato R" (calcolato) e l'angolo R"VV" (calcolato),

    sarebbe utile determinare il lato VR" o l'angolo ß di conseguenza il valore di x è facilmente determinabile.

    Il compito è complicato!

    Ho pensato di applicare le equazioni di rette nel piano del triangolo:

    • equazione della retta passante per i punti R e V (facilmente calcolabile)
    • equazione della retta passante per  R" o V' (ma di  questi due ultimi punti non si conoscono le coordinate)
    • equazione della retta passante  per R' e V (facilmente calcolabile)

    dalle intersezioni delle retta si potrebbe calcolare la lunghezza VR" che permetterebbe di calcolare facilmente x

  12. Vincenzo Zappalà
    23/12/2019 at 15:27

    caro Michele,

    sì, la faccenda è un po' più complicata. Nella soluzione che ho pensato io (ma potreste trovarne di migliori) non si fa uso di coordinate cartesiane, ma solo di formule trigonometriche e di una piccola equazione finale...

  13. Fabrizio
    23/12/2019 at 20:21

    Non ho trovato una soluzione trigonometrica. Ho pensato anche io ad una soluzione con le coordinate cartesiane. In figura ci sono gli elementi principali del procedimento.

    Il sistema di coordinate che ho utilizzato ha l'asse y lungo BV e l'asse x lungo VR".

    In figura ci sono le equazioni delle rette che hanno alle loro intersezione i punti incogniti V' ed R".

    Da queste intersezioni ricavo le coordinate di V' e R" espresse in termini di m e n, i coefficienti angolari delle due rette. Da queste coordinate ricavo la distanza al quadrato tra i due punti che è fissata a 1 essendo un dato del nostro problema.

    Questa è una equazione con la sola incognita m, essendo n nota.

    Purtroppo è una equazione di 4° grado. Teoricamente risolvibile algebricamente, ma molto complessa.

    Per questo l'ho risolta numericamente con il risultato per m in figura.

    Dalle coordinate di B e V' ricavo la distanza tra i due punti, l'incognita del nostro problema, che dipende solo da m.

    Una volta nota m posso ricavare il valore di questa distanza.

  14. Fabrizio
    23/12/2019 at 23:03

    Questa figura corregge quella inviata con il messaggio precedente.

    L'errore era nella trascrizione della espressione di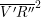  \dpi{100} \small \overline{V'R''}^2.

     

  15. Vincenzo Zappalà
    24/12/2019 at 06:48

    Bel lavoro, ovviamente... ma io continuo a preferire la soluzione puramente trigonometrica...

    Lo lascio ancora un po' in evidenza, tanto ci sono le feste... e se qualcuno vuole ancora pensarci... ben venga!

    AUGURI!!!

  16. Fabrizio
    27/12/2019 at 03:00

    Nella figura ho messo la soluzione trigonometrica che ho trovato.

    I lati e gli angoli di questa parte della figura possono essere tutti ricondotti a funzioni dell'angolo β.

    I lati del triangolo rettangolo, BR" e BV, per la definizione stessa delle due funzioni trigonometriche.

    L'applicazione del teorema dei seni al triangolo VV'R'' da l'espressione di VV' (prima riga sotto il grafico).

    Lo sviluppo dell'applicazione del teorema di Carnot al triangolo BVV' con angolo in V (seconda riga) porta ad una equazione di 4° grado in cos(β) (penultima riga).

    La soluzione reale positiva di questa equazione è nell'ultima riga con la lunghezza che cerchiamo.

    Non sono riuscito ad evitare l'equazione di 4° grado. Ho provato anche altri metodi applicando il teorema di Carnot in modo diverso o derivando l'equazione da una ulteriore applicazione del teorema dei seni. Tutti i tentativi sono finiti in una equazione di 4° grado.

     

  17. Vincenzo Zappalà
    27/12/2019 at 06:51

    Caro Fabri,

    sei in linea con me! Io, però, ho lavorato con la distanza x e alla fine mi rimane come soluzione possibile x3 = 2. In realtà, l'equazione di quarto grado può facilmente ridursi, mettendo in evidenza x e raccogliendo...

    Il risultato è, comunque, giusto! Bravo!!!

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.