Categorie: Matematica
Tags: equazione quarto grado geometria quiz soluzione trigonometria
Scritto da: Vincenzo Zappalà
Commenti:0
Soluzione del triangolo impossibile ***
L'esercizio va risolto solo con la trigonometria. Ciò non toglie che alla fine si ottenga un'equazione di quarto grado, la quale, però riesce a essere risolta con estrema facilità. Un bravo a Fabrizio...
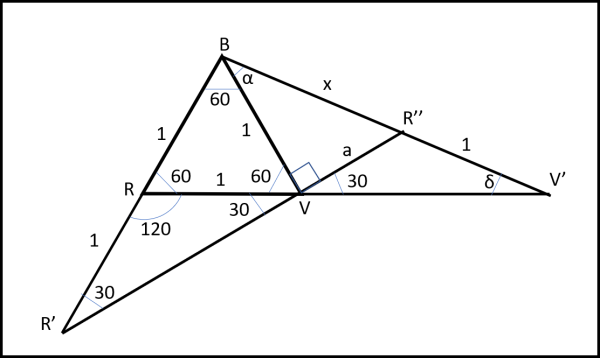
Iniziamo con la figura che illustra la situazione e indica gli angoli e i segmenti conosciuti e non conosciuti.
Il segmento x è ciò che vogliamo trovare. Sapendo che il triangolo BRV è equilatero di lato 1, abbiamo subito che i suoi angoli sono di 60°. Il triangolo RR'V è per costruzione un triangolo isoscele, con l'angolo in R pari a 120° (180° - 60°), da cui segue che RVR' = 30 °. Sarà ugualmente uguale a 30° anche l'angolo R''VV', in quanto opposto al vertice. Infine, BVR'' risulta essere un angolo retto, dato che 180° = BVR" + 30° + 60°.
Consideriamo il triangolo rettangolo BVR''. Chiamiamo a il lato VR'' (incognito) e α l'angolo in B (incognito). Possiamo scrivere, applicando il teorema dei seni:
x/sen (90) = a/sen α
x = a/sen α .... (1)
Consideriamo, adesso, il triangolo VR''V' e applichiamo nuovamente il teorema dei seni, chiamando δ l'angolo in V' (incognito):
1/sen(30) = a/sen δ
a = 2 sen δ .... (2)
Sostituendo la (2) nella (1), otteniamo:
x = 2 sen δ/sen α .... (3)
Passiamo al triangolo BRV' e facciamo la somma dei suoi angoli:
180° = α + 60 + 60 + δ
α + δ = 60 °
δ = 60 - α .... (4)
Inseriamo la (4) nella (3) e otteniamo :
x = 2 sen (60 - α)/sen α ... (5)
Ricordando la formula relativa al seno della differenza, possiamo scrivere:
x = 2 sen δ/sen α = 2 sen(60 – α)/sen α = 2(sen 60 cos α – cos 60 sen α )/sen α = 2 ((√3/2) cos α – ½ sen α )/sen α x = √3 cos α/sen α - 1 .... (6)
Passiamo nuovamente al triangolo rettangolo BVR " e applichiamogli il teorema di Pitagora:
x2 = 1 + a2
a = √(x2 – 1) .... (7)
Ma possiamo anche scrivere:
tan α = a/1
a = sen α/cos α
cos α/sen α = 1/a = 1/√(x2 – 1) .... (8)
Ricordiamoci la (6) e sostituiamo cos α/sen α con quanto dice la (8)
x = √3 cos α/sen α - 1 = √3 /√(x2 – 1) - 1
x = √3 /√(x2 – 1) - 1 .... (9)
(x +1) √(x2 – 1) = √3
Quadrando ambo i membri si ha:
(x +1)2 (x2 – 1) = 3
(x2 + 1 + 2x)(x2 – 1) = 3
x4 + x2 + 2x3 – x2 - 1 – 2x = 3
x4 + 2x3 – 2x – 4 = 0
Sembrerebbe -anzi è- un'equazione di quarto grado, che, però, non è difficile rendere facilmente trattabile:
x3(x + 2) - 2(x + 2) = 0
(x + 2)(x3 - 2) = 0
L'equazione è uguale a zero quando è zero una delle due parentesi di sinistra...
Tuttavia, dato che siamo in un piano euclideo non possiamo certo accettare una soluzione negativa, ossia x = - 2. Rimane solo la possibilità:
x3 = 2
che porta alla sola soluzione accettabile
x = 21/3 ≈ 1.26
Ovviamente, ci saranno altri procedimenti che portano allo stesso risultato, ma l'importante è aver trovato un triangolo veramente preparato!
QUI trovate il quiz