Un semplice problema geometrico ci dà l'occasione di utilizzare un metodo apparentemente più lungo e faticoso, ma di grande interesse per casi molto più complicati. Sconfiniamo nella teoria degli insiemi, ma in modo decisamente elementare.

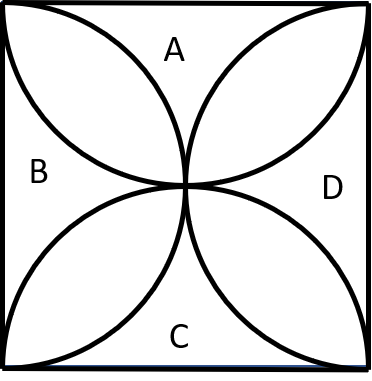
Il problema da risolvere è veramente semplice, oltre che molto bello esteticamente... Dobbiamo solo avere a disposizione 4 semicerchi tutti uguali e combinarli tra loro in modo da far apparire una specie di "fiore" con quattro petali. Esattamente ciò che viene mostrato in Fig. 1.

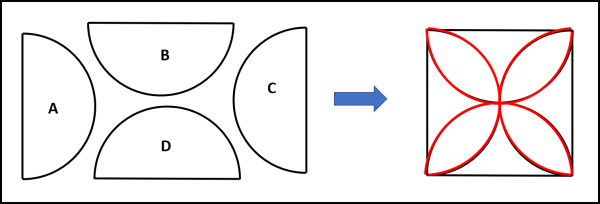
Lo scopo è quello trovare l'area del "fiore" conoscendo il diametro a dei quattro semicerchi.

Beh... è un gioco veramente da ragazzi. Basta considerare un quarto della figura, dopo aver tracciato le diagonali del quadrato che contiene il fiore e che ha lato uguale ad a. Otteniamo quanto riportato in Fig. 2.

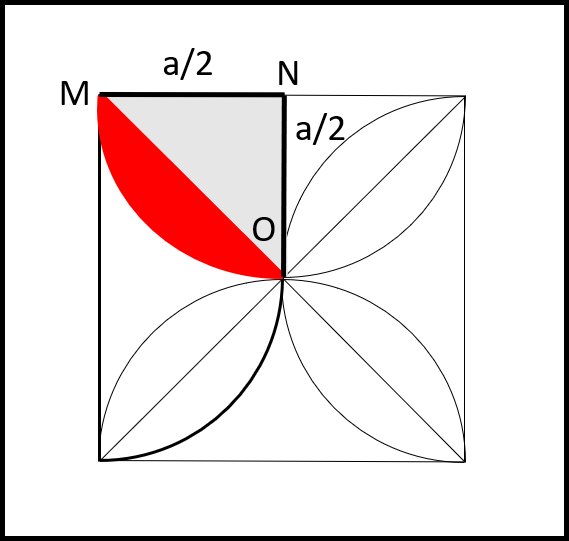
Per avere l'area di mezzo petalo basta calcolare l'area del settore circolare MON e sottrargli l'area del triangolo rettangolo MNO:

Area mezzo petalo = ¼ πa²/4 - a²/8

Il fiore è composto da 8 mezzi petali e, quindi:

Area fiore = 8(¼ πa²/4 - a²/8) = ½ πa² - a²

Area fiore = a²(π/2 - 1)

Bene... tutto fatto. Però, però... sarebbe bello complicarci un po' la vita e risolvere il problema utilizzando gli insiemi e un paio di operazioni. Come insiemi di partenza prendiamo i 4 semicerchi A B C e D di Fig. 1. Insiemi sì, ma contenenti cosa? Potremmo dire tutti i punti che stanno al loro al loro interno o, più semplicemente, l'area.

No, non voglio certo entrare nei dettagli e nelle moltissime proprietà degli insiemi, regno indiscusso del nostro Umberto, ma solo utilizzarli per via grafica, ricavando la formula che interessa nel nostro caso, suggerendo soltanto come essa possa divenire qualcosa di ben più generale e importante.

Ricordiamo solo la definizione di alcuni simboli...

Con A intendiamo l'area dell'insieme A

Con A ∪ B intendiamo l'insieme che contiene o i punti di A o i punti di B. Lo possiamo chiamare UNIONE, dato che considera una e una sola volta i punti dei due insiemi. In pratica è l'area della figura composta dai due insiemi A e B.

Con A ∩ B intendiamo l'insieme che contiene i punti appartenenti sia ad A che a B. Lo possiamo chiamare INTERSEZIONE, dato che considera solo i punti che appartengono a entrambi gli insiemi. In pratica, è l'area della figura che i due insiemi hanno in comune.

Introduciamo anche la somma di due insiemi, ossia A + B. In questo caso intendiamo proprio la somma delle due aree, il che vuol dire che  l'area in comune viene considerata DUE volte.

Per comprendere meglio di che operazioni stiamo trattando, nei tre settori in cui vengono divisi i due insiemi inseriamo un numero che sta a indicare quante volte un dato settore è stato contato. Per l'UNIONE e l'INTERSEZIONE abbiamo solo il numero 1, per la somma abbiamo 1 per i settori separati e 2 per quello in comune (contato due volte).

Per maggiore chiarezza mostriamo quanto detto in Fig. 3 (Umberto non se la prenda per spiegazioni così banali ...)

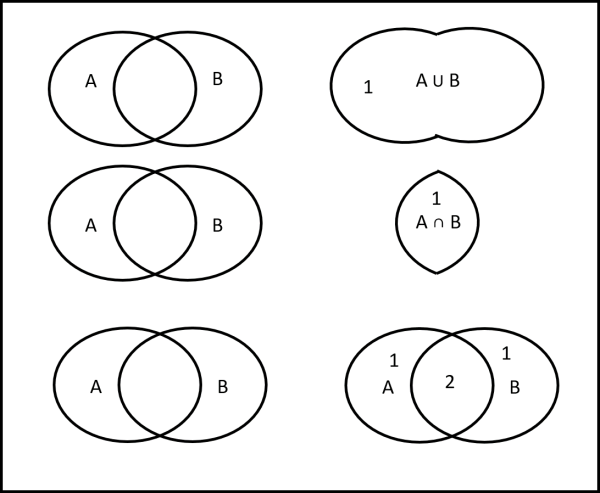
Con queste poche nozioni possiamo iniziare a costruire una relazione molto importante tra insiemi, ossia quella che lega la somma con l'unione e l'intersezione. Nel caso di due insiemi la descrizione è veramente banale. Possiamo scrivere:

A ∪ B = A + B - A ∩ B

La prova, in questo caso, è facilissima. Per ottenere l'unione di due insiemi basta sommare i due insiemi e poi togliere la loro intersezione. Per eccesso di chiarezza illustriamo graficamente il procedimento in Fig. 4

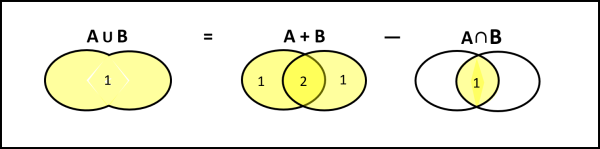
La faccenda si complica leggermente se andiamo a considerare tre insiemi A B e C. Vediamo, prima, la procedura in Fig. 5. La descriviamo passo dopo passo e poi la scriveremo con i simboli.

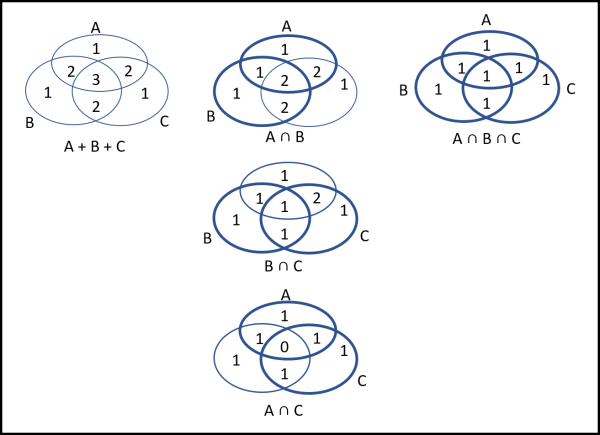
Come nel caso precedente, lo scopo è di ottenere l'unione dei tre insiemi, utilizzando la somma e la intersezione. Il primo passo è quello di sommare i tre insiemi (prima colonna da sinistra). Facendo questa operazione (A + B + C) assegniamo ad ogni settore (6 in tutto) della figura un numero che corrisponde al numero di volte che quel dato settore è stato contato. Noi vogliamo, invece, giungere a una figura che abbia il numero 1 in ogni settore (ossia all'unione). Cominciamo a togliere dalla somma l'intersezione tra A e B (prima immagine in alto della seconda colonna). Facendo questa operazione i numeri delle parti in comune scendono di una unità (il 2 e il 3 diventano 1  e 2), Continuiamo togliendo anche l'intersezione tra B e C (seconda immagine della seconda colonna) e il 2 e il 2 diventano 1 e 1. Finiamo col togliere anche l'intersezione tra A e C ottenendo che il 2 e l'1 diventino 1 e 0. A questo punto tutti i settori, tranne quello centrale, hanno il numero 1 (ossia la loro area appare una sola volta). Non ci resta che passare alla terza colonna e aggiungere l'intersezione tra A, B e C, in modo da mettere 1 anche nell'ultimo settore, quello comune a tutti e tre gli insiemi. Tutti i settori hanno il numero 1 per cui abbiamo ottenuto proprio l'unione dei tre insiemi, come si voleva.

E' facile scrivere la relazione che riassume le operazioni fatte:

A ∪ B ∪ C = A + B + C - (A ∩ B + B ∩ C + A ∩ C) + (A ∩ B ∩ C)

Non ci resta che aggiungere un insieme, ossia lavorare con quattro insiemi. Avrei potuto anche dare questo esercizio come "quiz", ma all'inizio del nuovo anno voglio essere clemente (potreste sempre mettervi alla prova con 5 insiemi...). Disegniamo la Fig, 5 e seguiamo i vari passaggi che ripetono quelli precedenti con piccole modifiche.

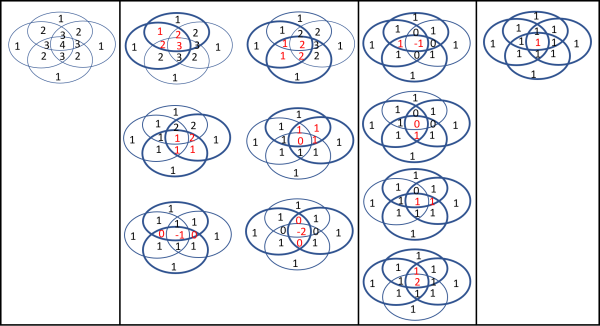
La figura è stata divisa in quattro parti. Nella prima abbiamo la solita somma degli insiemi, Nella seconda vi sono le 6 intersezioni tra gli insiemi a due a due (da sinistra a destra e dall'alto in basso); nella terza le 4 intersezioni tra gli insiemi a tre a tre, nell'ultima l'intersezione tra tutti e 4 gli insiemi. Alla prima parte (somma) togliamo le 6 intersezioni della seconda parte; al risultato sommiamo le 4 intersezioni della terza; al risultato togliamo l'intersezione dei 3 insiemi. Il risultato è una figura in cui i vari settori (dodici) hanno tutti il numero 1, ossia abbiamo proprio l'unione dei 4 insiemi.

Per ogni passaggio si sono scritti in rosso i numeri che sono stati cambiati o sottraendo o sommando. Notiamo che compaiono anche numeri negativi. Ciò vuol solo dire che abbiamo tolto quel settore più di una volta...

La formula finale può sintetizzarsi come segue:

A ∪ B ∪ C ∪ D = A + B + C + D - (A ∩ B + B ∩ C + C ∩ D + A ∩ D  + A ∩ C + B ∩ D) +                                        + + (A ∩ B ∩ C + B ∩ C ∩ D + A ∩ C ∩ D + A ∩ B ∩ D) - A ∩ B ∩ C ∩ D

Non è difficile intuire il proseguimento per un numero di insiemi crescenti: si tolgono e si aggiungono intersezioni di insiemi fino a che non si raggiunga l'intersezione di tutti gli insiemi. Noi non la riportiamo dato che entrerebbero in gioco simboli più complicati... ma chi fosse interessato agli insiemi può andare QUI.

Noi, invece, possiamo continuare nella nostra ricerca di una soluzione diversa per il problema iniziale. Infatti, ci ricordiamo bene che siamo partiti con quattro "insiemi", ossia con quattro semicerchi uguali, A, B , C e D. Riprendiamo la figura a fiore e analizziamola da un nuovo punto di vista (Fig. 6).

Proviamo allora a scrivere la formula ricavata precedentemente e utilizzarla per il nostro caso:

A ∪ B ∪ C ∪ D = A + B + C + D - (A ∩ B + B ∩ C + C ∩ D + A ∩ D  + A ∩ C + B ∩ D) + (A ∩ B ∩ C + B ∩ C ∩ D +          A ∩ C ∩ D + A ∩ B ∩ D) - A ∩ B ∩ C ∩ D

A ∪ B ∪ C ∪ D non è altro che l'unione dei quattro semicerchi, ossia l'area del quadrato.

A + B + C + D non è altro che l'area totale dei 4 semicerchi, ossia due volte l'area del cerchio di diametro a

La somma delle intersezioni di quattro semicerchi presi due a due dà proprio l'area dei quattro petali del nostro fiore (A ∩ B,  B ∩ C, C ∩ D e A ∩ D) , mentre  A ∩ C  e  B ∩ D hanno intersezione zero, non avendo nessun punto in comune. Le intersezioni a tre a tre danno nuovamente come risultato un area uguale a zero, dato che non hanno alcuna parte in comune. Lo stesso capita anche, a maggior ragione, per l'intersezione dei quattro semicerchi.

La formula si riduce, nel nostro caso, a:

A ∪ B ∪ C ∪ D = A + B + C + D - (A ∩ B + B ∩ C + C ∩ D + A ∩ D  + )

Area del quadrato di lato a = area di due volte il cerchio di diametro a - area del fiore

Area del fiore =  2 a² π/4 - a²

Area del fiore = a²(π/2 - 1)

C. V. D.