Andiamo a vedere come la nostra formica viola ha risolto il problema dello scoglio e si è impossessata del magnifico diamante.

Innanzitutto, ricordiamo ancora che siamo nel pianeta TEORIA, dove non esiste l'attrito e dove anche l'equilibrio instabile può considerarsi stabile. Aggiungiamo a tutto ciò il fatto che la formica non ha peso e che riesce a fare piccoli salti non superiori a un decimo di unità.

Intellix guarda bene i mattoni e si accorge che sono proprio  lisci, uguali e perfettamente regolari. Prende un mattone, lo poggia sul terreno (ovviamente liscio) e lo spinge verso l'esterno in modo che stia ancora in equilibrio. La formica sa benissimo dove viene a cadere il baricentro del mattone e non si sorprende che metà del mattone resti sospesa in aria verso lo scoglio. Non basta di certo, dato che la distanza è di 2 unità e lei ha solo ottenuto un avanzamento di 1/2 unità. Tuttavia, la strada è quella giusta...

Intellix ricorda molto bene la formula che permette di determinare il baricentro di due oggetti e ha solo bisogno di stabilire un sistema di coordinate x e y che abbia una certa origine. Come origine prende il bordo del precipizio e la x va verso lo scoglio, mentre la y è la verticale.

Solleva il primo mattone e poi inserisce sotto di lui un nuovo mattone. Fa in modo di far coincidere il bordo esterno del secondo mattone proprio con l'origine degli assi (Fig. 2 a sinistra), in modo che il baricentro del primo (x_B1 ), che cade nel punto di mezzo del mattone, coincida con l'origine.

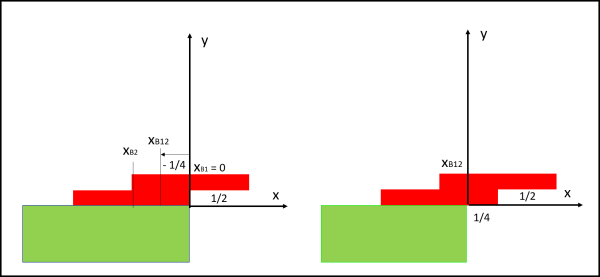
A questo punto deve calcolare il baricentro dei due mattoni e farlo esattamente coincidere con il limite del precipizio. L'equilibrio sarà instabile, ma tanto basta su TEORIA. Non gli resta che scrivere (le masse dei mattoni sono tutte uguali all'unità):

x_B12 = (x_B1 m₁ + x_B2 m₂)/(m₁ + m₂)

Nel nostro caso diventa:

x_B12 = (0 · 1 - 1/2 · 1)/2 = - 1/4

Per mettere in equilibrio i due mattoni e far coincidere il nuovo baricentro con l'origine, basta spostare il tutto di 1/4 lungo l'asse x verso destra. Abbiamo la configurazione della Fig. 1, a destra. L'equilibrio è instabile, ma alla formica poco importa. La distanza del bordo destro del primo mattone dall'origine (orlo del precipizio) vale adesso 1/2 + 1/4 = 3/4. Non basta ancora, ovviamente, ma è stato fatto un altro passo in avanti. Teniamo anche conto che l'altezza dei due mattoni è adesso uguale a 0.2 unità. La formica fa piccoli salti, ma riesce a saltare tranquillamente un decimo di unità e quindi può arrivare al bordo del secondo mattone.

Non resta adesso che ripetere l'azione precedente, considerando l'insieme dei mattoni 1 e 2 come mattone unico M₁₂. Sotto di lui mette un nuovo mattone M₃ in modo che abbia il bordo esterno a filo del burrone (Fig. 2, a sinistra).

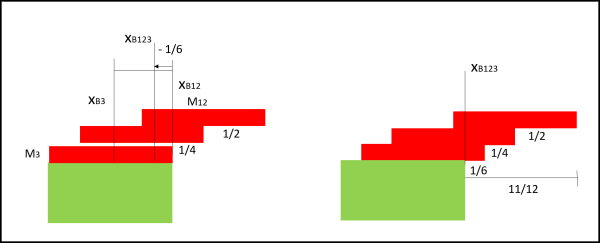
Calcola agevolmente  il nuovo baricentro tra M12 e M3:

x_B123 = (0 · 2 - 1/2 · 1)/3 = - 1/6

Nuovamente, per mettere in equilibrio i tre mattoni deve spostare il tutto di 1/6 verso destra (Fig. 2, a destra).

Avendo ora un mattone composto da tre mattoni, può facilmente proseguire e aggiungere un quarto mattone sotto i primi tre, trovando il nuovo baricentro:

x_B1234 = (0 · 3 - 1/2 · 1)/4 = - 1/8

Spostando il tutto verso destra di 1/8 la formica ottiene una lunghezza tra il bordo del primo mattone e l'origine pari a

1/2 + 1/4 + 1/6 + 1/8 = 25/24 > 1

Evviva, la formica è già riuscita a mettere in equilibrio 4 mattoni  e arrivare fino a una lunghezza maggiore dell'unità: ha superato metà della distanza dal bordo dello scoglio, che rimane, però, ancora troppo lontano e troppo alto, dato che l'altezza raggiunta è soltanto 0.4 unità. La formica non si arrende di certo e prosegue nel suo lavoro, sapendo che deve avere ancora molta pazienza...

Non vi è più bisogno di eseguire tutti i calcoli. E' semplice pensare come prosegue la scalata verso il diamante. Per ogni mattone aggiunto, lo scoglio si fa più vicino, anche se sempre più lentamente. Scriviamo quanto ottenuto attraverso la distanza d raggiunta dalla strana scala e immaginiamo di proseguire con lo stesso sistema usato dalla formica:

d_n= 1/2 + 1/4 + 1/6 + 1/8 + .... + 1/2n + ....

raccogliendo 1/2 si ha:

d_n = 1/2 (1 + 1/2 + 1/3 + .... + 1/n + ....)

Facendo un po' di conti si può facilmente ottenere il valore di n per il quale la lunghezza dello strano "ponte" sia proprio uguale a 2 unità. Per riuscirci servono n = 31 mattoni! Non solo, però,... 31 mattoni portano anche a un'altezza totale di 3.1 unità. La formica può adesso salire agevolmente e raggiungere il fantastico diamante! La Fig. 3 vede la sua opera completata...

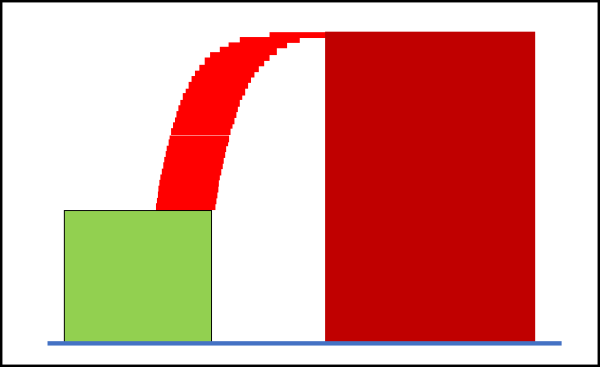
Non è  difficile ragionare in termini più generali. Come ormai conosciamo bene, la sommatoria che viene moltiplicata per 1/2 non è altri che la serie armonica, conosciuta da poco proprio grazie a un'altra formica. Sappiamo, perciò, che essa è divergente, ossia che, avendo tanti mattoni a disposizione, si può raggiungere qualsiasi luogo, accettando come stabile un equilibrio che è invece instabile (basterebbe un qualsiasi leggero disturbo per far crollare tutto il "ponte" di TEORIA). Magari raggiungere anche un altro pianeta... (ma le cose si complicherebbero per la gravità variabile...)-

L'argomento è stato studiato in dettaglio e, a titolo di esempio, mostriamo una costruzione molto più articolata che potrebbe raggiungere un equilibrio stabile. Tuttavia, sarebbe bene che i lavori non venissero affidati a coloro che hanno costruito l'autostrada Alessandria-Genova o Torino-Savona ( e non solo, purtroppo...).

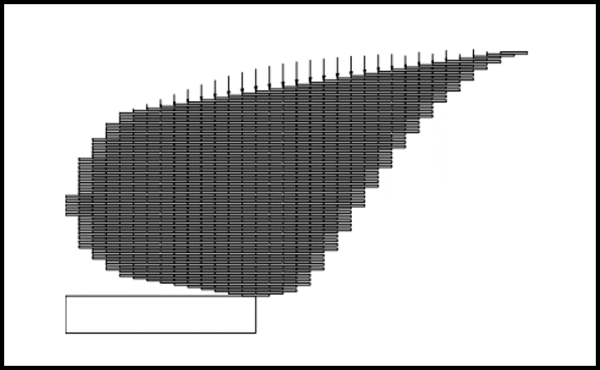
Il quiz lo trovate QUI

P.S.: complimenti, come sempre, a Fabrizio, la cui soluzione la trovate nei commenti, e i migliori auguri a Umberto per un rapido ritorno alla normalità.