Quiz: Un sindaco e un autista.****
Il nuovo sindaco di una piccola città del Veneto, neo eletto, come al solito cerca di dimostrare ai cittadini quanto promesso in campagna elettorale.Il motto è ordine, pulizia e risparmio.
 .............................................................
.............................................................
E' necessario pulire di continuo la rete stradale del piccolo comune. La rete stradale del comune è formata esclusivamente da 16 vie di lunghezza 1 km e 2 vie di lunghezza 2 km come nella figura:
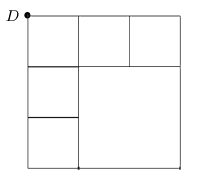
Il punto D schematizza il deposito da dove parte un furgone per il lavaggio delle strade strade.
Il sindaco si è accorto che l’automezzo per la pulizia delle strade consuma carburante per ben 24 km, ogni volta che parte per eseguire un lavaggio.

Porta quindi davanti al giudice l'autista con l'accusa di di furto di carburante.Ma l'autista, appassionato di matematica, afferma che il carburante consumato è necessario per uscire dal deposito, pulire tutte le strade e rientrare al deposito. Anzi, è anche il minimo percorso realizzabile. Secondo voi, il giudice a chi dà ragione?

Sulla scia dei minimi percorsi, vi propongo questo quiz, più logico però che matematico. Nessun conto da fare, a parte delle somme e delle moltiplicazioni. Quindi aritmetica base . Probabilmente ci sono diversi modi per risolverlo, ma il più elegante riguarda degli argomenti da me trattati in questo sito. Ma chiaramente ogni altra soluzione è ben accettata. Non c'è altro da dire. So che saprete valutare da soli le risposte, mentre il testo penso sia inequivocabile . Buon divertimento!






9 commenti
difficile o poco interessante? Parte del quiz può però essere risolto graficamente . Poi bisognerebbe ricordarsi dei ponti di Venezia..
Non do una vera risposta per lasciare spazio... Chi, però, volesse almeno verificare il 24, deve ricordare che
24 = 16 + 8 e che 8 vale 4 per 2. Non dico altro...
intanto grazie Vincenzo
Osservando la mappa della rete stradale si nota una bella simmetria diagonale che ci aiuta a ridurre la difficoltà del problema.
Basta trovare il percorso più semplice (breve) per andare dal punto di partenza, dove c'è il deposito, nell'angolo in alto a sinistra, al punto opposto, l'angolo in basso a destra. Poi, al ritorno, basterà seguire un percorso del tutto identico e speculare per rientrare al deposito
come si vede da questa figura, l'andata si compie percorrendo 12 Km e pulendo mezza città (due strade vengono percorse per due volte). La sequenza del percorso potrebbe essere diversa ma il numero di Km percorsi resterebbe il medesimo. Non si tratta di una dimostrazione matematica che il percorso è il più breve possibile, ma di una semplice verifica della affermazione dell'autista.
Come detto, il percorso di ritorno sarà strutturato nello stesso modo: lo vediamo nella seguente figura...
In totale sono stati percorsi 24 Km. Sembra proprio che l'autista sappia il fatto suo, al punto che, per il bene dei cittadini del comune veneto, non sarebbe male se l'autista prendesse il posto del sindaco e viceversa.
P.Il fatto che 4 vie da 1 km debbano essere percorse 2 volte è in sintonia con il messaggio cifrato di Vincenzo.
Complimenti a Umberto per averci proposto questo simpatico quiz.
ben tornato Oreste! Come ai vecchi tempi la tua lucidità intuitiva e sempre eccezionale. Si questa é la verifica dei 24 km. , se vedo bene dal disegno che é un po' sfuocato. Un po' più difficile é dimostrare che è il minimo.
caro Oreste... siamo sempre in sintonia!
per chi non trovasse l articolo citato:
http://www.infinitoteatrodelcosmo.it/2018/02/24/nove-ponti-venezia/
Rileggendo l'articolo citato da Umberto, http://www.infinitoteatrodelcosmo.it/2018/02/24/nove-ponti-venezia/ appare evidente nella conclusione ( parole di Eulero) che dovendo tornare al punto di partenza (il deposito D del mezzo che lava le strade) il grafo è percorribile, solo se tutti i suoi nodi sono di grado pari.
Osservando la mappa delle strade risulta evidente che ci sono ben 8 nodi che hanno grado dispari, essendo ciascuno di essi toccato da tre lati.
Collegando a coppie questi nodi con opportuni lati ne eleviamo il grado da 3 a 4. Ora avremo tutti i nodi di grado pari, al prezzo di avere introdotto 4 lati in più, ossia 4 km da percorrere in più dello sviluppo delle strade (che è di 20 Km)
La figura che segue illustra il passaggio al grafo percorribile ( aggiunta degli archi rossi) ed il percorso che dovrà essere seguito dal mezzo che lava le strade (tracciato in verde).
In definitiva, come dicono gli amici Vincenzo e Oreste, a sostegno di quanto affermato dall'autista, il numero di Km minimo è 24 ( e il sindaco farebbe bene a dare le dimissioni).
P.S. forse la dimostrazione non sarà molto rigorosa, sentiremo che ne dice Umberto, ma credo che dia già una idea di come procedere con il ragionamento.
sei super veloce Maurizio. il succo è proprio questo. Vediamo se qualcuno ha qualcosa da dire.
Perchè il minimo è 24? non potrebbe essere qualcosa di compreso fra 20 e 24?