Abbiamo cominciato con il principio di Archimede (che è in realtà un teorema), ma adesso facciamo un salto in avanti per poi ritornare al grande genio siracusano. Poche formule in più...

Come visto nell'articolo precedente (QUI), il principio di Archimede è in realtà un teorema e il vero principio stabilisce che la  "pressione" di una particella di un fluido è determinata dalla colonna dello stesso fluido che la sovrasta. Dobbiamo arrivare a cavallo tra XVI e XVII per averne una dimostrazione "rigorosa", quando l'eclettico fisico e ingegnere fiammingo Simon Stevin enuncia la sua legge sulla pressione dei fluidi. Una sacrosante conferma del principio di Archimede.

Un breve inciso del tutto personale. Stevin è diventato Stevino in tutti i libri di testo e -forse per mia ignoranza- non ne capisco il perché. Me la sono presa col fatto che l'italiano De La Grangia sia diventato Lagrange e devo fare lo stesso per un nome fiammingo italianizzato... E' come se chiamassimo Einstein "Einsteino" o Feynman "Feinmano"... Mi fa venire in mente penosi trascorsi storici. Ne segue che continuerò a chiamarla legge di Stevin.

Essa, nella sua forma più generale, ha questo enunciato:

La pressione, esercitata da una colonna di fluido con densità costante, aumenta in modo direttamente proporzionale alla profondità h, misurata dalla superficie libera del fluido.

Ricordiamo subito cos'è la pressione in termini "moderni": una forza (in modulo) per unità di superficie, ossia:

P = F/S

dove S è, appunto, la superficie su cui agisce la pressione. Ovviamente, la pressione uguaglia la forza per una superficie unitaria. Ricordiamo anche che la densità ρ non è altro che il rapporto tra la massa e il volume di un corpo.

Immaginiamo, allora, di avere a disposizione un certo recipiente cilindrico contenente, ad esempio, acqua (Fig. 1) e facciamo qualche calcoletto banale.

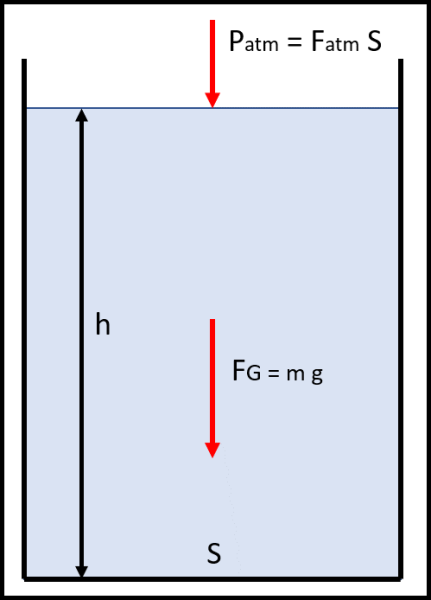
Quale sarà la pressione esercitata sul fondo del nostro contenitore di profondità h? Molto facile da calcolarsi considerando le forze in gioco: la forza esercitata dall'atmosfera sulla nostra superficie esterna più la forza di gravità del liquido. Entrambe sono dirette verso il basso e si possono perciò sommare:

F = F_atm + F_G

Tuttavia, possiamo facilmente esprimere le forze in funzione della pressione e scrivere la forza di gravità in funzione della massa del fluido, ossia:

F_G = P S = P_atm S + mg           .... (1)

Tuttavia abbiamo anche che:

m = V ρ

dove V è il volume dell'acqua, che vale superficie di base per altezza, ossia:

V = S h

sostituendo nella (1), otteniamo:

P S = P_atmS + gρSh

Ci accorgiamo che tutti i termini sono moltiplicati per S, per cui possiamo semplificare e scrivere:

P = P_atm + gρh            .... (2)

P_atm, g e ρ sono costanti, per cui la (2) dimostra  che la pressione varia in modo lineare con h, aumentando  al crescere della profondità.

Se avessimo considerato solo una particella di superficie infinitesima, avremmo ottenuto lo stesso risultato e quindi la pressione varia solo in funzione dell'altezza di una colonnina verticale di liquido, proprio come enunciato da Archimede. La legge mostra anche la pressione atmosferica, ma questo termine scomparirebbe se il contenitore fosse ermeticamente chiuso.

Archimede aveva proprio ragione: pur non conoscendo ancora la legge di gravitazione universale ne aveva sicuramente una certa idea in testa.

Un'analisi anche superficiale e puramente basata sul ragionamento fa già capire come salta fuori il teorema di Archimede. Parecchie volte sento ripetere la sua enunciazione in modo puramente mnemonico, ma il motivo per cui compare il peso dell'acqua spostata sembra un piccolo mistero. In realtà la faccenda è molto semplice.

Immaginiamo che al posto del corpo qualsiasi immerso nell'acqua ci sia un corpo composta da... acqua. E' ovvio, da quanto abbiamo appena detto, che la pressione nella parte inferiore del corpo di acqua deve essere maggiore di quella a cui è soggetta la parte superiore. Le parti laterali subiscono pressioni uguali e contrarie, per cui si possono annullare. Ne segue che l'unica forza in gioco, dovuta alla pressione, è quella che deriva dalla differenza tra pressione sulla faccia inferiore e sulla faccia superiore del corpo... acquoso. Questa è la famosa spinta di Archimede, capace di fare stare in equilibrio l'intero corpo acquoso. Per mantenere l'equilibrio è necessario, però, che questa spinta sia uguale alla forza peso del corpo fatto d'acqua (Fig. 2).

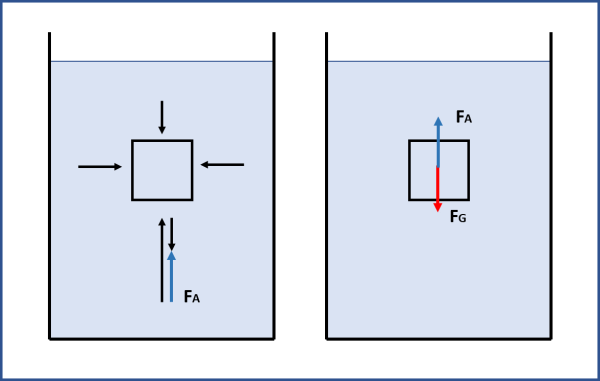
Ne segue che la spinta è proprio uguale al peso dell'acqua, che sarebbe spostata inserendo al suo posto un corpo diverso dall'acqua. A questo punto, abbiamo di fronte due alternative:

(1) la densità del corpo è maggiore di quella dell'acqua, la sua forza peso supera la spinta e il corpo va a fondo;

(2) la densità è minore e allora vince la spinta che lo fa risalire verso l'alto.

Vedremo, comunque, in dettaglio le varie situazioni e le condizioni di galleggiamento. Basta, comunque, pensarci un po' sopra e ci si arriva anche senza molte formule.

Gli altri articoli dedicati al Teorema di Archimede li trovate QUI