Categorie: Fisica classica Matematica
Tags: fuga lago mostro Pippo velocità
Scritto da: Vincenzo Zappalà
Commenti:34
Il mostro del lago ***
Un problema di fisica e di matematica a cui ho dato una risposta. Tuttavia, penso che si possa fare ancora meglio, almeno in termini di rapidità. Forza, dateci dentro.... Una bella trota a chi risolverà l'enigma.
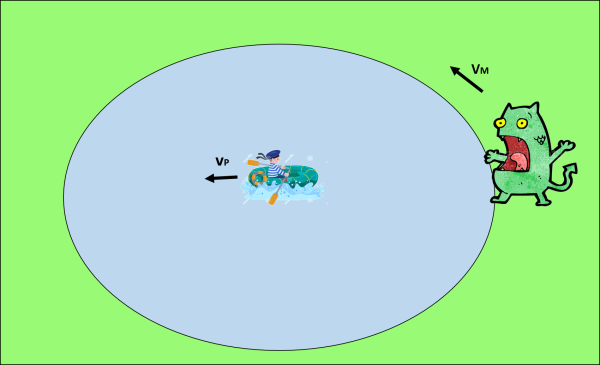
Come riuscire a sfuggire al mostro del lago? Questo è il grave problema del nostro amico Pippo che non vorrebbe concludere tragicamente la sua giornata di pesca...
Pippo ama pescare (anche se ributta in acqua tutti i pesci che cattura) e, appena può, raggiunge il "Lago del Mostro", ricchissimo di trote e dalla forma perfettamente circolare (raggio uguale a R), mettendosi esattamente al centro.
Conosce quel nome sinistro, ma, ovviamente, lo giudica una vecchia leggenda. Purtroppo, un brutto giorno, quando all'imbrunire decide di tornare a casa, si accorge con sgomento che la leggenda non è una leggenda! Sulle rive del lago ecco apparire un mostro sicuramente carnivoro che non vede l'ora di fare un solo boccone di Pippo.
La situazione è molto critica, dato che la velocità v, con cui può muoversi Pippo, remando, è inferiore a quella del mostro che corre lungo il bordo del lago. Il mostro, fortunatamente, non può entrare nel lago non sapendo assolutamente nuotare. D'altra parte, Pippo è un corridore molto abile e se raggiungesse la sponda anche un attimo prima dell'arrivo del mostro riuscirebbe sicuramente a distanziarlo e a salvarsi.
La domanda è:
"Qual è la velocità massima del mostro che permette ancora la salvezza di Pippo?"
La velocità deve essere data rispetto a v e, ovviamente, bisogna descrivere la strategia adottata da Pippo.
P.S.: in realtà, vi sono tre strategie che portano a un certo risultato...
La prima è decisamente banale e porta a un certo valore di vM (1 asterisco)
La seconda è un po' più articolata e riesce ad aumentare la velocità (tra 2 e tre asterischi)
La terza è un miglioramento della seconda, comporta un po' più di fatica (3 asterischi buoni), ma aumenta ancora un po' la velocità limite del mostro.
La soluzione la trovate QUI
34 commenti
Rompo io il ghiaccio, va
Prima strategia: Pippo parte dal centro e rema in direzione diametralmente opposta alla posizione iniziale del mostro. Remando a velocità (costante) v, percorrerà lo spazio R che lo separa dalla riva in un tempo pari a R/v. Nel momento in cui Pippo inizia a remare, anche il mostro inizia a muoversi, capendo che Pippo sta andando in direzione a lui diametralmente opposta. Lo spazio che lo separa da quella che sarà la posizione finale di Pippo è, dunque, una semicirconferenza, di lunghezza
R. Il tempo che impiegherà a percorrere questa distanza muovendosi a velocità (costante) vm lungo la riva sarà 
R / vm.
Perché Pippo si salvi, il tempo impiegato dal mostro per percorrere la semicirconferenza dovrà essere minore a quello impiegato da Pippo per percorrere la distanza dalla riva . Quindi:
da cui, semplificando R e invertendo alla fine ottengo:
Possiamo lavorare sempre in termini di K = vM/vP. Semplificherà le cose...
ops.. mi accorgo solo ora, rileggendo il mio commento, che in questa frase:
"Perché Pippo si salvi, il tempo impiegato dal mostro per percorrere la semicirconferenza dovrà essere minore a quello impiegato da Pippo per percorrere la distanza dalla riva ."
ho sbagliato a scrivere "minore" al posto di "maggiore", come in realtà si capisce subito dopo dalla disequazione riportata. Quindi, ovviamente, il tempo impiegato dal mostro deve essere maggiore di quello impiegato da Pippo.
ovviamente Artù... ma nel seguito è meglio lavorare sull'uguaglianza come caso limite...
Ho provato a trovare una soluzione cercando di bilanciare due componenti del moto della barca. La strategia seguita dalla barca prevede prima un diversivo per nascondere al mostro la reale destinazione finale della barca. Quando il mostro non può più avvantagiarsi della conoscenza della destinazione della barca, procedere direttamenete verso la destinazione. Ci sono due soluzioni con una diversa durata del diversivo. Una lo porta avanti fino a che è possibile, l'altra anticipa la fine del diversivo. Rimango nel vago per non condizionare altri risolutori del quiz ed avere il tempo per preparare qualche figura.
Scrivo sotto in caratteri bianchi le velocità limite che ho ottenuto nei due casi.
1) vm<v (1+π)=v 4,14..
2) vm<v 4,39...
caro Fabry...
il diversivo ha una sua chiara caratteristica. Le seconda che hai detto non mi torna... comunque vedremo...
Come ho detto, comunque, la mia soluzione non mi piace moltissimo, per cui altre vie sono ben accolte! Per aiutare Pippo questo e altro !!!
quello che non ho capito è se il mostro può cambiare anch'esso strategia in funzione di quella di Pippo. Ovvero, Pippo cambia direzione e il mostro cambia anch'esso verso, dovendo restare sempre sul cerchio che limita il lago. Non so se ho chiesto una banalità. Il mostro è un essere intelligente?
Sì, il mostro è intelligente e Pippo deve metterlo di fronte a scelte logiche.
ma non conosce la fisica e la matematica, vero ?
la conosce, ma deve fare del suo meglio per prendere Pippo.
Non riesco a capire bene cosa intendi dire con cambiare la strategia.
andare in un verso piuttosto che Nell altro.
libero di farlo... ma anche Pippo...
Supposto che Pippo si muova in direzione radiale dal centro del lago di raggio R verso il bordo e che il mostro si muova sul bordo della circonferenza del lago di raggio R , percorrendo una semi circonferenza, ed ammesso che inizino a muoversi entrambi allo stesso istante se si verifica l'incontro sul punto di intersezione della traiettoria di Pippo e quella del mostro (semicirconferenza) sarà passato lo stesso tempo t dall'inizio. In tali condizioni la velocita del mostro
Vm e quella di Pippo V sono date da
Vm= πR/t
V = R/t
dalle quali
t = πR/Vm
t= R/V
Vm = πR/t e V = R/t
la Vm>V nello stesso tempo il mostro deve percorrere una distanza maggiore di Pippo.
questo è il caso limite in cui le due velocità differiscono per il fattore π.
Se non si incontrassero ovvero Pippo riesce ad arrivare alla riva un istante prima del mostro sarebbe sufficiente che il valore del fattore di proporzionalità sia inferiore a π ovvero un numero che al limite si approssimi per difetto a π,. in tali condizioni la velocita del mostro sarebbe ancora maggiore di quella di Pippo
OK Michele, questo è il primo passo, ma si può fare di meglio...
Nella realtà bisogna pure considerare la fase successiva all'approdo di Pippo:
Per non farsi raggiungere a terra deve avere una velocità maggiore del mostro deve perciò correre a terra più velocemente del mostro altrimenti....
Un'altra possibilità è quella di continuare per la tangente dopo il diversivo.
Se la barca facesse questo percorso, il mostro dovrebbe avere una velocità di circa 4,6 volte quella della barca. Finora è la migliore che ho trovato. Tra quelle che nella seconda parte sono rettilinee dovrebbe essere la migliore. Non si può andare oltre perchè altrimenti il mostro cambierebbe verso della sua corsa.
Forse ci potrebbe essere qualche traiettoria non rettilinea anche dopo il diversivo che da un migliore risultato.
caro Michele,
un attimo prima... possiamo tranquillamente simularlo con l'arrivo contemporaneo (cos+ usiamo il segno uguale e semplifica la trattazione).
Caro Fabry,
come al solito fai come Cirano... e giunto al fine della licenza TU tocchi! Hai già scritto le formule? Mi piacerebbe vederle dato che io temo di essere andato per le lunghe. Magari tu hai sveltito i calcoli... Comunque, il diversivo può avere un andamento ben definito e senza perdite di tempo... Sulle linee curve (finali) penso proprio che non facciano che peggiorare.
Secondo me Pippo deve usare una strategia che gli permetta di approdare sulla terraferma in un tempo sufficiente per poter poi correre ed allontanarsi dal mostro:
sia t =1 il tempo comune con il quale i due si incontrano sul punto diametralmente opposto alla posizione iniziale del mostro, Pippo non approda torna indietro verso il centro, il mostro vista la mossa prosegue pensando che Pippo si porti sulla sponda opposta sapendo di essere più veloce e quindi lo aspetterebbe al varco sulla sponda opposta.
Ma Pippo arrivato al centro anziché proseguire sul diametro si sposta in direzione perpendicolare "in alto" rispetto alla figura del guiz, il mostro allora procede sulla circonferenza credendo che Pippo voglia approdare sulla sponda intersezione del raggio normale al diametro "orizzontale" della figura sapendo sempre che arriverebbe prima di lui essendo più veloce.
ma Pippo appena percorso 1/4 del raggio verso l'alto inverte la sua direzione si dirige verso il centro del cerchio e poi svolta verso la posizione con la quale si sarebbero incontrati alla prima tappa.
in questa ultima fase Pippo percorre una distanza totale:
1/4 R + R = 5R/4
il tempo che impiega per approdare è
Tp = (5R/4) / Vp essendo Vp = R avendo supposto unitario il tempo comune del primo incontro
Tp = (5R/4) /R = 5/4 = 1,25
Il mostro per raggiungere Pippo dovrà spostarsi per 3/4 dell'intera circonferenza impiegando un tempo totale
Tm = (πR + πR/2) / πR la velocita del mostro per la supposizione fatta è πR
Tm = (3/2πR) / πR = 3/2 = 1,5
Pippo arriva prima sulla sponda con un margine di tempo pari a 1,5 - 1,25 = 0,25 e può scappare sulla terraferma.
Caro Michele,
La strategia è molto meno soggettiva e non è basata su quello che penserebbe il mostro, ma è definita in modo esatto. Ti ripeto che mostro e Pippo possono anche arrivare insieme sulla sponda e Pippo è libero, considerando anche solo una frazione di secondo di vantaggio...
Osservo che la strategia basata unicamente sulla curva di elusione (diversivo) e non sui movimenti decisi dal mostro, conduce alla conclusione che Pippo si salva solo se K (velocità del mostro rapportata a quella di Pippo) è inferiore o uguale a 4,6.
Quindi se il mostro ha una velocità 5 volte maggiore di Pippo sembrerebbe che questi non abbia via di scampo.
Tuttavia, riprendendo la domanda di Umberto sulla logica seguita dal mostro, supponiamo che il criterio che utilizza (il mostro) sia quello di prevedere il punto di approdo in base alla direzione della barca e di scegliere l'arco di cerchio più breve per correre verso di esso.
In questo caso Pippo potrebbe condizionare gli spostamenti del mostro costringendolo a muoversi entro certi limiti, mentre la barca si avvicina progressivamente alla riva verso un approdo sicuro.
Mi sembra che questa fosse l'idea di Michele, anche se nel suo intervento era finalizzata a far giungere Pippo con un certo anticipo a riva, piuttosto che a salvarlo dalle grinfie di un mostro veloce oltre il limite di K=4,6.
Lasciando da parte le formule, propongo solo un semplice grafico in scala con l'ipotesi di un mostro 5 volte più veloce di Pippo (K=5) che osserva dove va la barca, prevede il punto di approdo e vi converge percorrendo l'arco più breve dalla sua attuale posizione.
Nel disegno il raggio del lago è stato fissato a R=6,4
Il punto A è posizionato in modo che l'arco superiore da M1 verso A sia di un infinitesimo più breve dell'arco inferiore. Il punto B è posizionato in modo che l'arco di destra da M2 verso B sia un infinitesimo più breve dell'arco di sinistra.
Inizialmente Pippo si muove dal centro del lago verso A, stimolando il mostro ad andare verso quel punto seguendo il percorso superiore. Quando il mostro si trova in M2 ha percorso la distanza 10 e Pippo la distanza 2.
A questo punto Pippo vira verso il punto B. Il mostro inverte anche lui la marcia ( B è più vicino andando in senso orario). Ma nel momento in cui il mostro arriva in M1, Pippo cambia di nuovo rotta e si dirige verso A.
Ora il mostro si trova nella condizione iniziale e torna sui suoi passi lungo l'arco che lo porta a passare per M2.
La rotta di Pippo continua ad alternare la destinazione A e la destinazione B, mentre il mostro resta confinato tra i punti M1 ed M2.
Progressivamente la distanza della barca dalla riva decresce finché risulta inferiore al valore 2 che rappresenta il "passo" della linea spezzata. In quel momento Pippo punta decisamente alla riva e si salva, perché il mostro, anche trovandosi nel punto più favorevole M2, non riuscirà a superare in tempo il punto A, ben distante dall'approdo.
Nella figura questo passo finale è il numero 8. l'arco di cerchio di raggio 6,4 -2 = 4,4 segnale il momento in cui è possibile dirigersi a riva senza pericolo. In realtà nel momento in cui la rotta interseca questo arco è possibile andare immediatamente a riva ( nel disegno il punto di intersezione risulta leggermente in anticipo sul nodo 7)
Questa strategia "adattativa" consente quindi di salvare il soldato Pippo anche quando K>4,6.
Probabilmente si potrebbe anche riuscire,ma parliamoci chiaro, tutti i tratti da 1 a 6 sono inutili in quanto Pippo può sempre arrivare a un certo punto, dipendente da K, avendo sicuramente il mostro diametralmente opposto. Parlare di infinitesimi per far pensare il mostro e decidere di conseguenza mi sembra un po' una forzatura. Non era questo lo scopo.
Avrei molto più piacere che mi spiegaste, con le dovute formule, perché la velocità massima (senza troppi tentennamenti e cambi di direzione) è uguale a 4.6...
In origine la domanda era ...
"Qual è la velocità massima del mostro che permette ancora la salvezza di Pippo?"
seguita dalla richiesta di spiegare la strategia, enunciando tre possibilità.
Esiste però anche questa ulteriore strategia che consente la salvezza di Pippo per qualsiasi velocità del mostro.
Per quanto riguarda il posizionamento di A e B gli "infinitesimi" sono una condizione sufficiente ma non necessaria, vanno solo collocati in modo che il mostro capisca bene qual è il percorso più breve e quello più lungo. Del resto è la stessa semplificazione introdotta dicendo che Pippo si salva "per una frazione di secondo di vantaggio"
Invece...
Potresti spiegare meglio, restando nel caso concreto di K=5, come Pippo può arrivare al punto 7 avendo sicuramente il mostro diametralmente opposto, senza i "tentennamenti" che lo fanno correre avanti e indietro? Perché, se così fosse, il limite K=4,6 sarebbe superabile.
d'accordo, d'accordo... può anche darsi che funzioni (ho qualche dubbio, però e non ho tempo per pensarci adesso). Secondo me Pippo non può girovagare ovunque, ma entro limiti ben ristretti. Può darsi che mi sbagli, però...
In ogni modo finora mi è stata solo spiegata e dimostrata la massima velocità di 3.14. E le altre inferiori a 4.6 ??
Mettiamo a posto queste e poi penseremo al zig zag o anche alla cicloide...
A meno che la strategia che indichi tu sia sempre valida, anche con 3 e 4... potresti dimostrarlo con un caso pratico e numerico... La strategia fino a 4.6 può essere generalizzata benissimo.
non ho provato a rispondere perché ancora non capisco bene cosa di può fare e cosa no
bisognerebbe inquadrare il problema in un formalismo matematico più stretto. Prendiamo il caso più semplice illustrato da Arturo; e mettiamo che il mostro vada molto più veloce di pgreco •v. Il mostro sorpassa il punto opposto diametrale e cosa fa? Torna indietro?si ferma?Oppure la velocita é tale che arrivi proprio dove arriva Pippo allo stesso istante .pippo va a finirgli in bocca o calcolando cambia Direzione? Possono oscillare così intorno ad un ipotetico punto di approdo? Non avrò capito niente ma per me suddetta velocità non si.può definire.
Secondo me, superato un certo limite ben determinabile, il mostro valuta la componente del moto di Pippo lungo l'asse che passa per lui e per Pippo e riesce comunque a raggiungerlo, senza bisogno di invertire la marcia.
Ripeto ancora... il mostro sa che se Pippo supera un certo limite riuscirà sempre a catturarlo, per cui se ne frega dei diversivi e punta dritto continuando nella sua corsa. Quello che conta è la parte di raggio rettilinea che Pippo riesce a percorrere da un certo punto in poi: se questa non gli permette di salvarsi, il mostro non si cura dei diversivi e continua dalla stessa parte...Il mostro sa fare i calcoli...
Anche io non riesco a capire la strategia che deve usare Pippo per salvarsi dal mostro.
Ammesso che sia lecita la soluzione che prevede che i due si incontrino nel punto diametralmente opposto al punto di partenza del mostro e per la quale si è calcolata la velocità massima del mostro nella ipotesi che siano partiti allo stesso istante dalle rispettive posizioni iniziali. Questa procedura di calcolo e considerando unitario il tempo occorrente per l'incontro a portato alle due velocità nel punto di incontro
Vm = πR
Vp = R
ora nel "punto di incontro" le due velocità sono due vettori perpendicolari tra loro e con moduli come sopra.
Ritengo che il mostro non possa superare in modulo la velocità πR, mentre Pippo svincolatosi dal laghetto possa benissimo aumentare il valore in modulo R della sua velocità (con le proprie forze si corre più velocemente a terra che in acqua).
Quindi il modulo di Vm rimane costante ma Vm può cambiare direzione, Vp può cambiare sia in modulo che in direzione.
Mi sembra lecito pensare che il mostro dovendo rincorrere Pippo assuma la stessa sua direzione del moto se così affinché Pippo si salvi deve accadere Vp > Vm ( nei rispettivi moduli).
Quale sarà la direzione comune se questa è la strategia?
Ho fatto la verifica grafico numerica per alcuni valori di K in base alle seguenti ipotesi
assumiamo che:
Per ora non posto le figure ma i risultati sono questi…
Caso K =3,33 spezzata formata da 2 segmenti di 30 metri + uno di 10 metri + uscita finale di 30 metri
Totale percorso barca 100 metri. Il mostro ne ha fatti 300 avanti e indietro + 33 che non sono bastati a farlo arrivare al punto di sbarco.
Caso K = 4 spezzata formata da 2 segmenti da 25 metri + uno di 22 metri + uscita finale di 25 metri
Totale percorso barca 97 metri. Il mostro ne ha fatti 300 avanti e indietro + 88 , senza riuscire ad avvicinarsi al punto di sbarco.
Caso K=4,6 spezzata formata da 4 segmenti di 21,7 metri + uno di 17 metri + uscita finale di 21,7 metri
Totale percorso barca 125,5 metri Il mostro ne ha fatti 500 avanti e indietro + 78 verso l’approdo senza arrivare abbastanza vicino in tempo.
Conclusioni
Per i casi con K minore o uguale a 3,14 la linea di fuga è costituita da un solo segmento, ossia il raggio che dal centro va verso il punto diametralmente opposto alla posizione iniziale del mostro.
Al di sopra di K =3,14 e fino a K= 4,6 la soluzione con diversivo (la immagino come una spirale che parte dall’origine e poi viene abbandonata quando la distanza dalla sponda è uguale alla lunghezza di arco che deve percorre il mostro / K) dovrebbe essere più efficiente di quella costituita dalla spezzata a zig zag , ossia la lunghezza del percorso totale dalla barca ( e il tempo trascorso) è più breve. Ma in ogni caso il risultato è garantito anche seguendo la spezzata.
Per valori di K maggiori di 4,6, credo che l’unica alternativa per non essere catturati sia quella della rotta a linea spezzata che fa correre il mostro avanti e indietro.
Ora però mi chiedo se è vero che i due si muovano sempre alla loro massima velocità, oppure possono scegliere una velocità diversa che ritengono più conveniente, o addirittura fermarsi, o tornare indietro, come dice Umberto nel suo commento.
Inoltre come ragiona il mostro? Potrebbe intuire la strategia e adeguarsi? Ad esempio non farsi ingannare dalla direzione momentanea e scegliere un percorso che lo porti più vicino alla posizione attuale della barca, trascurando la brevità?
La situazione non è simile a quella di un inseguimento missilistico di un bersaglio (in cui la tattica base di elusione è quella di sequenze di "break" , ossia brusche virate di 90° a destra e sinistra). Nel caso del mostro e di Pippo, quest'ultimo, se le cose si mettono male, ha sempre la possibilità di azzerare tutto riportandosi al centro del lago e provare da capo una nuova strategia.
Capisco che il succo del quiz non è tanto di trovare la strategia per salvare Pippo in ogni caso, ma di trovare la velocità massima del mostro a cui si possa sfuggire seguendo una certa curva. Fino a quella velocità si riesce ad uscire dal lago qualunque cosa faccia il mostro (è davvero così?). Oltre quella velocità è necessario sapere bene come ragiona il mostro altrimenti non c'è modo di uscire dal lago. Bene, trovate questa curva e mandate un sms a Pippo dicendogli cosa deve fare, oppure, se il mostro è 4,6 (+ qualcosa) volte più veloce della sua barca ( ma come si può saperlo a priori?), che smetta di remare e aspetti l'elicottero dei pompieri.
Ultima alternativa, se se la sente, provare a remare a zig zag nel modo e nei tempi descritti. Se non funziona meglio fermarsi prima della riva.
Caro Mau,
siamo arrivati alla stessa conclusione.
Quello che chiedo ancora e a cui nessuno risponde è : "Come riuscite a calcolare 4.6?" io ci sono arrivato, ma penso si possa fare meglio...
La traiettoria che porta al rapporto limite vm/v=4,6 è quella nella figura sotto.
Questa traiettoria funziona se il mostro è poco intelligente e considera sola la posizione istantanea della barca. Nella figura il discrimine è la linea ideale verde che congiunge mostro e centro del lago e ruota con il mostro. Il mostro continua a correre in senso antiorario perché vede la barca da quella parte della linea o sulla linea.
Il ragionamento che ho fatto è il seguente.
Nella gara tra barca e mostro quello che conta è la distanza angolare tra mostro e barca. La traiettoria della barca dovrebbe cercare ritardare il recupero della distanza angolare da parte del mostro. Per mantenere inalterata la distanza angolare con il mostro la barca dovrebbe mantenere la stessa velocità angolare del mostro.
Per semplificare ragiono in un caso normalizzato dove il raggio del lago R è 1 e la velocità del mostro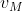
è 1 anche essa. Questa scelta non da' problemi perché contano solo i rapporti v/vM e r/R. Indico con r e v la posizione radiale della barca e la sua velocità.
La velocità angolare del mostro è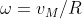
. Per mantenersi al passo con il mostro, la barca deve avere la stessa velocità angolare, che corrisponde ad una componente della velocità nella direzione tangenziale alla riva 
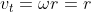. La prima parte della traiettoria, quella circolare, fa proprio questo.
Poichè la velocità della barca è v, per la componente radiale rimane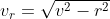
Quindi la barca procede con componente angolare della velocità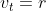
e velocità radiale 
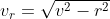. In questo modo avanza verso la riva, ma non fa avvicinare il mostro. Questo funziona fino ad un certo punto. Più la barca avanza radialmente, meno rimane per la velocità radiale. Quando r diventa numericamente uguale a v, la barca non riesce più ad avanzare verso la riva (
).
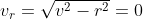Questo punto viene raggiunto con il mostro che ha percorso 90° e la barca si trova a 270° rispetto alla posizione di partenza del mostro indipendentemente dalla velocità v. (Non riporto qui la dimostrazione di questo e del fatto che la traiettoria è una semicirconferenza).
Occorre cambiare strategia. Una possibilità è quella di andare in linea retta verso la riva. Ma in quale direzione. Per vedere quale è la direzione ottimale ho supposto che la barca vada in una direzione generica puntando verso un punto della riva che gli permetta di guadagnare ancora un angolo
(linea rossa più leggera)
Calcolo quale è in vantaggio/svantaggio
rispetto al mostro all'arrivo (l'espressione è nella figura). 
è una funzione crescente di 
(almeno così appare graficamente nell'intervallo che ci interessa).
Per questo conviene mettere
al massimo, quello che non fa mai attraversare la linea verde ideale tra centro e mostro. Quindi la traiettoria è quella che prosegue per la tangente con )
e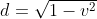 
. La velocità limite è quella che porta 
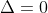. Quindi occorre risolvere questa equazione:
La soluzione numerica di questa equazione da v=0,2172.. che è l'inverso del rapporto che cerchiamo
1/v=4,603...
Caro Fabry,
si capisce abbastanza bene... ma non mi compare l'ultima figura. E' colpa del mio PC o del tipo di figura?
Più o meno concordiamo, senza bisogno di strani zig-zag che non riescono certo a disorientare il mostro. In fondo, è un mostro molto intelligente che sa accettare la sconfitta. D'altra parte che cosa potrebbe fare? Tornare indietro non gli converrebbe più e se andasse dalla parte giusta, Pippo andrebbe dall'altra parte.
La prima immagine te la rubo per la soluzione!
L'ultima figura è quella con il grafico. La bande in fondo non sono figure. Non so perchè siano apparse.
La figura la cedo volentieri.
grazie e ... come sempre... grande!