Qui trovate il quiz e le soluzioni nei commenti. Due parole sulla soluzione, anche se non servirebbe. Intanto la giustificazione dei quattro asterischi per la soluzione completa, ovvero che il percorso indicato dall'autista è quello minimo. Questo era riservato a chi trovasse una soluzione autonoma, indipendente dal teorema di Eulero, che abbiamo visto qui. Nei commenti è stata dimostrata la validità del percorso di 24 KM, sia graficamente (Maurizio) che con l'uso dell'aritmetica (Vincenzo). Manca forse la dimostrazione che 24 Km è il minimo percorso.  Il citato teorema di Eulero da parte di Maurizio afferma che , se dobbiamo partite dal deposito D e tornarci percorrendo solo una volta i tratti del disegno seguente, i nodi dispari devono essere zero.

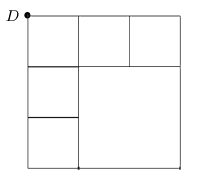
risulta dunque impossibile che il percorso sia di 20 KM, ovvero la somma di tutte le strade da pulire. I nodi dispari sono infatti 8.

L'autista deve allora invertire la marcia su certi tratti, per creare un nuovo grafo che parte da D e torna in D, e fare in modo che il grafo finale abbia zero nodi dispari. Rubo allora il disegno di Maurizio:

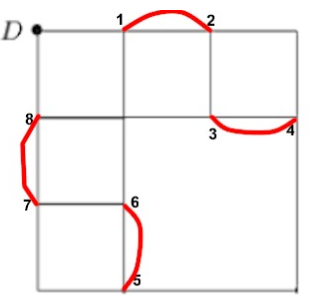
Ragioniamo direttamente di su di esso , senza indicare i versi di percorrenza, ma sfruttando solo Eulero.Eulero infatti non si preoccupa di esplicitare il percorso, che potrebbe essere molto più complesso di questo, ma solo della parità dei nodi. In questo grafo, tutti i nodi hanno grado pari; quindi zero nodi dispari. Quindi il grafo è percorribile da D a D, ed ha lunghezza 24 Km. Si può fare di meglio? No, perchè dobbiamo trasformare i nodi 1,2,3,4, 5,6,7,8 in nodi pari. Questo è possibile farlo in modo minimo,  aggiungendo un lato che unisce due nodi contigui con un totale di soli quattro nuovi lati, che rappresentano altrettante inversioni di marcia. SE aggiungessi solo 1,2,o 3 lati non trasformerei tutti i nodi dispari in nodi pari.