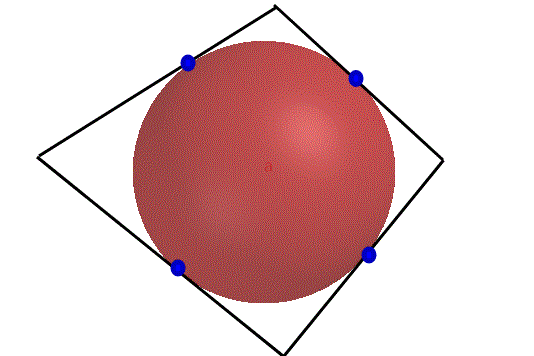
Sto cercando disperatamente di proporre dei quiz che siano risolvibili anche dal cellulare, quindi privi di disegni e calcoli complessi. Lasciamo per un pò perdere poi l'esposizione romanzesca, per essere più precisi, come lo vuole la matematica (anche perchè in questo caso non avrei idee per scriverla). Abbiamo a che fare con una figura sbilenca è una simmetricamente perfetta; cosa succederà ai punti di contatto se si tenta di incastrare una nell'altra?
Questo breve articolo è stato sollecitato da un commento di un nostro lettore che ha escogitato (in modo fin troppo complicato) un esperimento mentale capace di dimostrare che si può superare la velocità della luce. In realtà, vorrebbe dimostrare che la stessa luce riesce ad andare più veloce della luce. Purtroppo, c'è un profondo errore nel ragionamento ed Einstein si salva ancora!
Un articolo un po' più tecnico dei precedenti, che purtroppo presuppone la conoscenza delle derivate. Tuttavia ciò ci permetterà di sfatare definizioni e formalismi tipici della geometria differenziale, quali i tensori metrici e gli elementi di linea infinitesimi. Ricordiamoci che il nostro scopo è quello di capire come vivere all'interno di una varietà dove di euclideo resta ben poco. In ogni caso, però, tramite il piano tangente possiamo ridurci sempre ad esso.
Questo articolo è estremamente interessante e l'argomento ben poco analizzato (finora almeno). Probabilmente apre un nuovo "mondo" di studi. Leggetelo, quindi, con molta attenzione e mettetevi alla prova. Come forse avrete immaginato, il riferimento al golf non è così forte come si sarebbe potuto credere. Lo scopo era di scuotere un po' il nostro Frank sempre in lotta per scalare posizioni (e anche per prenderci un po' in giro). Che anche lui "scenda" al nostro livello, forse un po' troppo teorico per un tecnogolfista...
Eccovi la mia soluzione che vuole essere un esercizio di fisica (poca) e tanta matematica (in particolare trigonometria). Come già detto, si può probabilmente sveltire il procedimento, ma non è certamente sbagliato.