Questo articolo (che vuole rispondere alla domanda posta QUI) è estremamente interessante e l'argomento ben poco analizzato (finora almeno). Probabilmente apre un nuovo "mondo" di studi. Leggetelo, quindi, con molta attenzione e mettetevi alla prova. Come forse avrete immaginato, il riferimento al golf non è così forte come si sarebbe potuto credere. Lo scopo era di scuotere un po' il nostro Frank sempre in lotta per scalare posizioni (e anche per prenderci un po' in giro). Che anche lui "scenda" al nostro livello, forse un po' troppo teorico per un tecnogolfista...

Sequenza di Linus e Code Golf

La sequenza di Linus può essere decritta sinteticamente come una sequenza di Vero e Falso (o 1 e 0, o 1 e 2, in vari testi) in cui ogni nuova entrata è scelta per evitare che si origini una sequenza. Se sono più di una si evita quella più lunga.

In parole più semplici viene chiamata la sequenza rompi-sequenza.

All’atto pratico si cerca di minimizzare ogni ripetizione.

In qualche modo (più stretto di quanto sembri) si riallaccia al Code Golf, un codice che nasce per competizioni di programmazione al computer. Il termine Code Golf deriva dalla somiglianza con lo sport del golf. In quest’ultimo i partecipanti cercano di raggiungere l’obiettivo attraverso il minimo numero di “tiri”, ossia minimizzando il punteggio acquisito. Un obiettivo che va contro molti altri sport in cui si cerca di massimizzare il punteggio. Nel golf code, invece, si cerca di ridurre il numero di “colpi” necessari a scrivere un programma.

La sequenza di Linus ha una forte analogia con il code golf, in quanto anche lei cerca di minimizzare le ripetizioni, ossia ridurre, in altre parole, il numero di colpi. Il fatto è che la sequenza di Linus e la sua “compagna” sequenza di Lucy, hanno aperto un nuovo mondo di studi che si è allargato a macchia d’olio, arrivando a ipotizzare mille altre applicazioni, come si può vedere nelle Conclusioni.

Costruiamo la sequenza di Linus

Cerchiamo di spiegare bene come la sequenza si origini, dato che il meccanismo è meno semplice di quanto sembri a parole. Lo scopo è di evitare momenti di “stasi” troppo lunghi, ossia annullare qualsiasi ripetizione troppo dispersiva, così come nel gioco del golf si cerca di evitare tiri inutili, dovuti ad errori o a valutazioni approssimative, tali da fare aumentare il numero di tiri necessari per arrivare in buca. In entrambi i casi si evitano inutili ripetizioni (se la pallina finisce in una pozza d’acqua devo uscire dall’acqua… molto meglio superare la pozza d’acqua).

Prima di entrare nella parte matematica vera e propria, ricordiamo come nasce “storicamente” la sequenza di Linus. Dobbiamo riferirci alle quattro vignette che seguono e che vedono Linus affrontare un test in cui le varie affermazioni possono essere vere o false.

Linus, lavorando con la sua logica e avvalendosi dell’esperienza acquisita, scrive una serie di risposte (Vero o Falso), senza nemmeno leggere il testo. La  storia di Schulz ha poco a che vedere con la vera sequenza di Linus, ma ne ha dato lo spunto, soprattutto nella seconda vignetta in alto a destra, quando Linus pensa: “The next one will also be False, to break the pattern (la prossima risposta deve ancora essere Falso, in modo da rompere la sequenza)”.

Il finale è nello stile meraviglioso e tipico dei Peanuts: “Se tu sei scaltro puoi passare un test di Vero o Falso senza essere troppo studioso”. In realtà, viene usato l’aggettivo smart che in inglese assume variazioni che vanno dalla furbizia all’intelligenza. In altre parole, potremmo intendere il “succo” come: “Se sei intelligente puoi fare a meno di studiare troppo” o, più drasticamente: “Se sei furbo puoi fare a meno di essere intelligente”. Insomma, scegliete voi la versione che più vi sembra esplicativa del pensiero di Linus.

Nasce quasi insieme anche la sequenza di Lucy, sempre pronta a criticare aspramente Linus, suo fratello minore, soprattutto per via della coperta che si trascina dietro (e un po’ anche per gelosia verso la furbizia del piccolo). La sequenza di Lucy, per ogni elemento aggiunto nella sequenza di Linus, riporta il numero di termini della sequenza ripetitiva che l’elemento di Linus ha interrotto. In qualche modo, la sequenza di Lucy aiuta a interpretare la sequenza di Linus.

Bando alle ciance, andiamo a scrivere la sequenza di Linus che è una e una sola…

Cominciamo con un Vero (V). Ovviamente questo primo elemento non crea e non interrompe nessuna sequenza

V

Se l’elemento seguente fosse V avremmo una ripetizione di un elemento, che è anche la più lunga ripetizione possibile. Ne segue che dobbiamo mettere F

VF

Se mettessimo F avremmo nuovamente una ripetizione di un elemento. Dovendo evitarla siamo costretti a inserire V

VFV

Se mettessimo V causeremmo una ripetizione di un elemento. Tuttavia, se mettessimo F causeremmo la ripetizione di due elementi (VF). Tra le due dobbiamo annullare la sequenza ripetitiva più lunga e quindi dobbiamo mettere V

VFVV

Se mettessimo V avremmo una ripetizione della sequenza di un elemento (V), ne segue che dobbiamo inserire F per romperla

VFVVF

Se mettessimo F avremmo la solita ripetizione di un elemento, ma se mettessimo V avremmo la ripetizione di una serie di tre elementi (VFV). Dobbiamo scegliere il male minore e, quindi, inserire F

VFVVFF

Se mettessimo F avremmo la solita ripetizione di un solo elemento, per cui scegliamo V

VFVVFFV

Se mettessimo V avremmo la ripetizione di un elemento, inseriamo perciò F

VFVVFFVF

Sembrerebbe ovvio inserire V per rompere la sequenza dell’elemento F, ma… attenzione, se mettessimo V, otterremmo il raddoppio della sequenza FV, per cui dovremmo inserire F. Inserendo F, però, raddoppieremmo una sequenza di tre elementi (VFF), Ne segue che V è la scelta giusta in quanto annulla la sequenza più lunga

VFVVFFVFV

Proseguiamo con F per impedire il semplice raddoppio di V? Eh no! Inserendo F avremmo la ripetizione della sequenza di due elementi (VF). Dobbiamo inserire V

VFVVFFVFVV

Possiamo Tranquillamente inserire F per interrompere la sequenza di un solo elemento, cioè V

VFVVFFVFVVF

Attenzione alla sequenza di tre elementi (VFV) che si sta per ripetere, quindi dobbiamo inserire F… meglio un elemento che tre. Ma siamo sicuri? Eh no … se mettessimo F ripeteremmo una sequenza con un numero maggiore di elementi (VFVVFF), ben sei! E’ obbligatorio mettere V.

VFVVFFVFVVFV

Interrompiamo subito la serie di V e inseriamo F? No, perché raddoppieremmo la serie di due elementi (VF). Però, però, se mettessimo V raddoppieremmo una serie di tre elementi (FVV). Torniamo sui nostri passi e accontentiamoci di F che ammette una serie di due, ma ne elimina una di tre.

VFVVFFVFVVFVF

Inseriamo V per rompere la serie di F? No, perché avremmo il raddoppio della serie di due (FV). Utilizziamo una F

VFVVFFVFVVFVFF

…..

Possiamo fermarci qui, dato che ormai la strategia dovrebbe essere chiara. Ma voi andate pure avanti… ogni passaggio abbisogna di un ragionamento che si fa sempre più articolato dovendo osservare attentamente le possibili sequenze più lunghe che possono essersi “preparate” con l’aumento degli elementi.

Ecco, comunque, la sequenza dei primi 500 elementi…

VFVVFFVFVVFVFFVVFVVVFFVFVVFFVVVFVVFFVFVVFVFFVVFVVVFFVFVVFFVFFFVVFVFFVVFFFVFFVVFVFFVFVVFFVFFFVVFVFFVVFFFVFFVVVFVVFFVFVVFVFFVVFVVVFFVFVVFFVVVFVVFFVFVVFVFFVVFVVVFFVFFFVVFVFFVVFFFVFFVVFVFFVFVVFFVFFFVVFVFFVVFFFVFFVVFVFFVVVFVVFFVFVVFVFFVVFVVVFFVFVVFFVVVFVVFFVFVVFVFFVVFVVVFFVFFFVVFVFFVVFFFVFFVVFVFFVFVVFFVFFFVVFVFFVVFFFVFFVFVVFFVFFFVVFVFFVVFVVVFFVFVVFFVVVFVVFFVFVVFVFFVVFVVVFFVFVVFFVVVFVVFFFVFFVVFVFFVFVVFFVFFFVVFVFFVVFFFVFFVVFVFFVFVVFFVFFFVVFVVVFFVFVVFFVVVFVVFFVFVVFVFFVVFVVVFFVFVVFFVVVFVVFFVFVVFFFVFFVVFV…

La sequenza di Lucy

Se avete notato, nella descrizione precedente, ho messo in grassetto la lunghezza di ogni sequenza massima che è stata interrotta. Possiamo riportare questi valori:

0 1 1 2 1 3 1 1 3 2 1 6 3 2 ….

Bene questa è la Sequenza di Lucy e, in pratica, spiega esattamente, passo dopo passo, quello che si è fatto scrivendo la Sequenza di Linus (il primo e unico 0 sta a significare che inserendo il primo elemento non si annulla nessuna sequenza).

La sequenza di Lucy ha anch’essa delle caratteristiche tutte da scoprire. Se considerassimo i suoi primi 1000 elementi, vedremmo comparire solo pochi numeri, ossia 0, 1, 2, 3, 4, 6, 8, 24, 30, 108.  Se passassimo a 1 000 000 di elementi, comparirebbe ancora un gruppo relativamente ristretto di numeri, ossia 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 24, 30, 36, 60, 72, 108, 318, 372, 414, 420, 444, 522, 528, 546, 552, 1280, 1292, 1298, 1632, 2620, 2752, 5876, 6203, 6218, 13912, 14312, 17220, 17580, 31532, 87650. Numeri che sembrano “quantizzati”. Che conoscano la meccanica quantistica? Forse no, ma cosa hanno di speciale 5876 oppure 17220 tali da farli comparire nelle sequenze di Linus da interrompere?

Confrontiamo Lucy e Linus

Altrettanto interessante è la trasformazione in grafico delle due sequenze. Nel caso di Linus adottiamo un semplice sistema: quando aggiungiamo V saliamo di una unità, quando aggiungiamo F, scendiamo di una unità. Si ottiene un interessante grafico…

La prima impressione, fermandosi a 40 elementi, è che la risposta V tenda a prevalere su quella F.

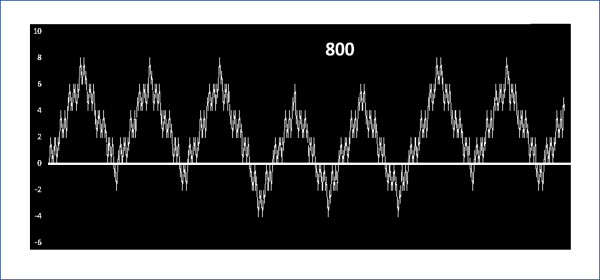
Ma è proprio così? Assolutamente no. Basta considerare il grafico per i primi 800 elementi. Un risultato a dir poco fantastico nella sua irregolare regolarità o nella sua regolare irregolarità

Quando l’elemento V sembra prendere il sopravvento ecco che l’F lo riporta a più miti consigli e viceversa.

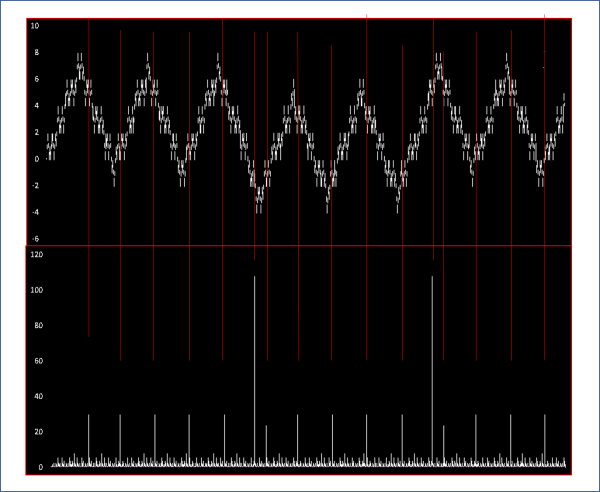
Estremamente interessante è confrontarlo con il grafico di Lucy. Una serie quasi continua di piccoli numeri, rotta improvvisamente da picchi solitari in altezza.

Non solo… ma questi picchi sembrano fortemente correlati ai massimi e ai minimi di Linus, come si vede nella figura che segue.

Conclusioni e discussione

Riportiamo letteralmente ciò che dice Wikipedia sul code golf:

“Il code golf è un gioco nel quale i partecipanti devono cercare di implementare un determinato algoritmo tramite un codice sorgente più contenuto possibile, in un linguaggio di programmazione che può essere specificato nel quesito ovvero scelto liberamente dai singoli partecipanti. Il nome è un riferimento al gioco del golf, nel quale l'obiettivo è completare le buche con un numero più basso di colpi.”

Poi continua:

“La minima lunghezza possibile di un programma (in un qualsiasi linguaggio) che produce un determinato output è nota come complessità di Kolmogorov, ed è stata introdotta da Andrej Nikolaevic Kolmogorov nel 1963. Il code golf è tuttavia più generale rispetto alla ricerca della complessità di Kolmogorov di un determinato output, in quanto non si limita al caso di programmi senza input e con un output specificato ma riguarda algoritmi che specificano una generica trasformazione input-output.”

Input - output = tiro iniziale - buca   -->  score

Questa è la versione più banale ed elementare del gioco del golf, in cui si cerca soltanto di mandare la pallina in buca con il minimo numero di tiri. Tuttavia non riesce a prevedere gli imprevisti, quali la sabbia, l’erba alta, l’acqua. In poche parole, se questi avvengono… il giocatore “normale” cerca di venirne fuori alla bene e meglio.

La sequenza di Linus, invece, è un code golf più sofisticato, in quanto anticipa proprio le anomale ripetizioni di tiri e le blocca sul nascere. Ogni caso va studiato a tavolino e memorizzato in modo che le conseguenze del tiro difettoso, per qualsiasi ragione sia avvenuto, abbiano già la loro storia profondamente radicata nel grande giocatore che applica immediatamente il blocco fornitogli dalla sequenza di Linus.

La sequenza di Lucy, che altro non fa che mostrare a quali pericoli è scampato Linus,  mostra, infatti,  cosa potrebbe succedere se una certa serie di ripetitiva di tiri non fosse bloccata sul nascere dalla sequenza di Linus, Ad esempio, nel caso della ripetizione di 6 elementi, Linus se ne accorge e corre ai ripari; Lucy ci mostra cosa ha evitato !

D'altra parte, dato che la sequenza di Lucy è anch'essa unica, basterebbe guardarla e memorizzarla per accorgersi dell'avvicinarsi di un grosso rischio "ripetitivo", che non sarebbe avvertito solo attraverso le sensazioni e l’emotività di un giocatore normale. Vi sarebbe il rischio di una ripetizione mostruosamente lunga che porterebbe a risultati disastrosi. Lucy avverte del rischio di effettuare un tiro che sembrerebbe "conveniente" e che invece porterebbe al verificarsi di un serie quasi senza uscita (pensiamo a quando i numeri di Lucy diventano altissimi).

Il grande campione ha studiato a lungo e sa come agire in anticipo e risolve con estrema eleganza, limitando i danni, una situazione che appariva senza uscita. La sequenza di Lucy “avverte”, prima posticipando leggermente i punti di massimo e minimo e poi anticipando le fasi più critiche. Una descrizione completa e interconnessa, atta a evitare e a prevedere il caos o, se preferiamo, un disastro golfistico.

Purtroppo, questo è un linguaggio compreso solo da pochi eletti del golf e -soprattutto- da coloro che fanno del golf non solo un gioco atletico, emotivo, quasi casuale, in cui ogni tiro dipende in qualche modo dal precedente, ma una vera trattazione matematica legata a una sequenza prestabilita che inizia nelle condizioni più adatte, in modo simile alle sequenze più classiche degli scacchi. Potremmo azzardare che il gioco della dama sta a un giocatore medio come il gioco degli scacchi sta ai Numeri Uno.

Pensate che stia dicendo sciocchezze o che stia dando troppa importanza a una banale sequenza? Ebbene no! Basta che andiate a leggere questo scritto, in cui si affronta in modo molto serio la sequenza di Linus e dove gli stessi autori si meravigliano del nuovo mondo che la sequenza sta aprendo. Chissà quali segreti nasconde ancora al suo interno e quali applicazioni potrà avere in fisica (entropia zero) o in Meccanica Quantistica (quantizzazione della sequenza di Lucy) o nella periodicità mascherata dei massimi e minimi della sequenza di Linus. Sicuramente un deciso passo in avanti rispetto alla banalità dei frattali…

P.S.: forse, nella foga della trattazione, ho esasperato qualche considerazione e/o conclusione, ma l’innovazione scientifica è fatta di esasperazioni. Che dire di Newton che, ESASPERATO dalle mele che continuavano a cadergli in testa, invece di comprarsi un cappello (giocatore medio), ha preferito spiegare PERCHE’ la Terra gira intorno al Sole (Numero Uno). E cosa pensare di Einstein che ESASPERATO dal veder cadere imbianchini, invece di contattare l’Ente per la sicurezza sul lavoro (giocatore medio), ha escogitato uno spaziotempo curvo (Numero Uno)?

Ai posteri l’ardua sentenza…

Chissà che Linus non diventi celebre come Fibonacci (QUI e QUI)?

La domanda la trovate QUI