In questo articolo cercherò di unire, come si suol dire, l'utile al dilettevole. L'argomento è quello dei satelliti geostazionari. Come noto, questi sono satelliti posti in orbita equatoriale attorno alla Terra ad una quota tale che essi, pur muovendosi rispetto ad un osservatore solidale con un sistema di riferimento posto nello spazio, risultano fermi in cielo rispetto ad un osservatore terrestre. Dico subito che, contrariamente ai comuni satelliti posti su orbite basse, quelli geostazionari non pongono problemi alle osservazioni astronomiche, proprio perchè risultano fermi rispetto a chi osserva il cielo da Terra. Non creano, quindi, se illuminati dal Sole, le odiatissime righe bianche sulle fotografie astronomiche del cielo notturno.

Tali satelliti geostazionari, qualunque sia la loro massa, hanno in comune un dato: la quota rispetto alla superficie terrestre, pari a circa 36000 km. La domanda che nasce spontanea è: perché proprio 36000 km ? Inoltre, come mai la loro massa è ininfluente ? La Fisica, come sempre, ci viene in aiuto.

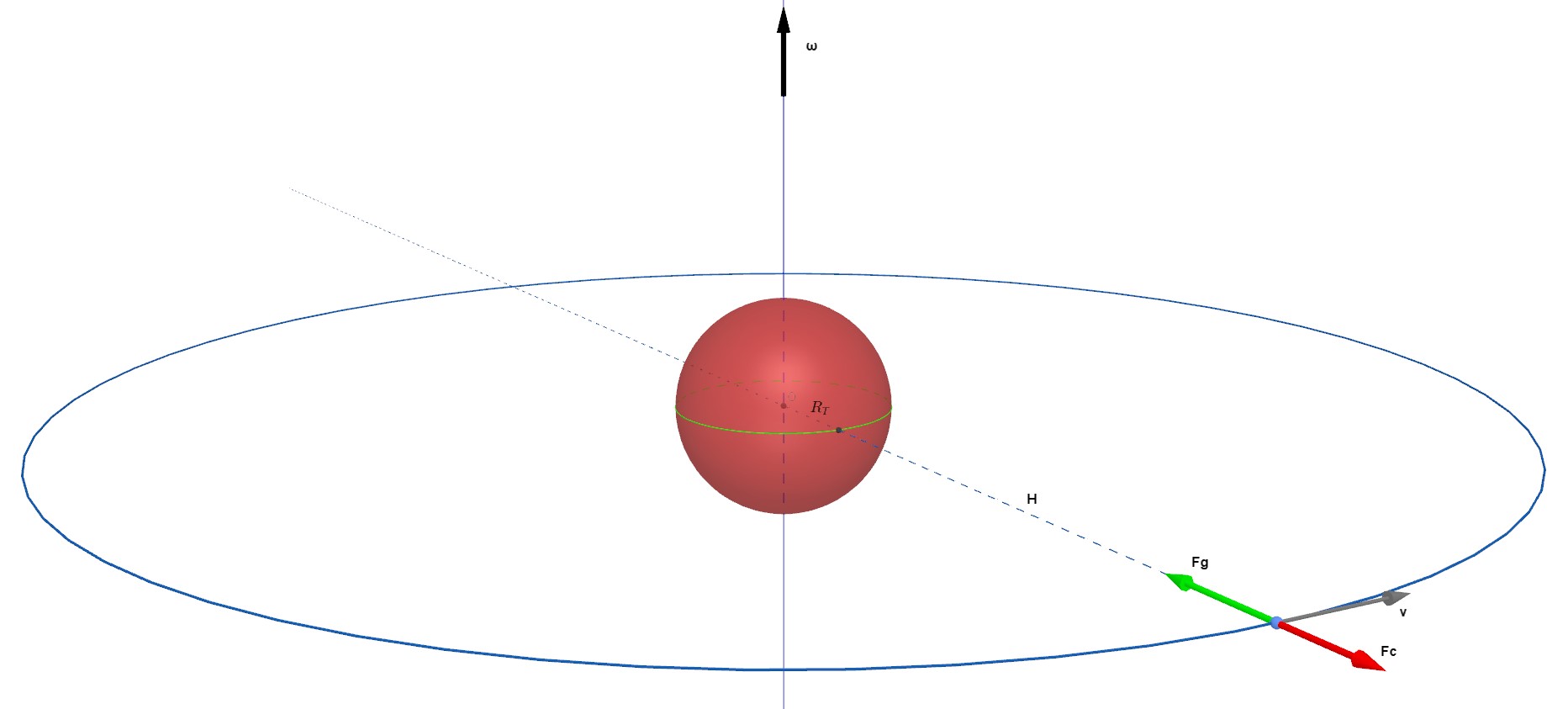
Consideriamo la seguente figura.

In essa è rappresentata in una visione prospettica la Terra (sfera al centro) e l'orbita circolare lungo cui si muove il satellite. Tale orbita giace nel piano equatoriale.

Ho indicato con Rt il raggio medio terrestre, pari a circa 6378 km, con H la quota del generico satellite geostazionario rispetto alla superficie terrestre, con v la velocità tangenziale del satellite, diretta, in ogni punto dell'orbita, secondo la tangente all'orbita. Sia, infine, m la massa del satellite.

Come è noto, un oggetto che si muove lungo una traiettoria circolare di raggio R con velocità tangenziale v è soggetto all'accelerazione centripeta data da:

          (1)

Inoltre, la velocità tangenziale v è legata a quella angolare  dalla relazione:

Per cui la (1) può anche scriversi come:

     (2)

Nel caso del satellite geostazionario posto a quota H dalla superficie terrestre, poichè il raggio della traiettoria seguita è pari alla somma del raggio terrestre e della quota del satellite rispetto al suolo, la suddetta relazione si scrive:

e la (2), quindi, si scrive come:

      (3)

La velocità angolare  è la stessa con la quale la Terra ruota attorno al proprio asse. Infatti la condizione che deve essere soddisfatta dai satelliti geostazionari è proprio che essi mi muovano nello spazio a velocità tale da risultare fermi rispetto a Terra. Devono, in pratica, ruotare attorno all'asse terrestre, con la stessa velocità angolare con cui ruota la Terra. Se avessero una velocità angolare diversa da quella della Terra, non risulterebbero più fermi in cielo per chi li osservasse da Terra, ma si muoverebbero in avanti o indietro rispetto all'osservatore a seconda del valore della loro velocità angolare.

Ora, la velocità angolare della Terra è presto determinata. La terra compie una rotazione completa (cioè di 2 radianti) attorno al proprio asse in circa 24 ore, ossia  86400 secondi. Quindi:

Quando facciamo ruotare attorno a noi un peso legato ad una corda trattenuta con una mano, sentiamo una trazione nella corda. Deduciamo, quindi, che se la corda venisse improvvisamente tagliata, il peso schizzerebbe via. E' come se la corda si contrapponesse ad una forza che tende a far schizzare via il peso. Nel caso dei satelliti geostazionari, il ruolo della corda viene svolto dalla forza di attrazione gravitazionale. In pratica, poichè in ogni istante il satellite geostazionario deve restare alla stessa quota rispetto alla superficie terrestre, la forza che tenderebbe a farli schizzare via, dovuta alla rotazione con velocità angolare  attorno all'asse terrestre, è, istante per istante,  controbilanciata dalla forza con cui il satellite e la Terra si attraggono. La prima è evidentemente data da:

dove m è la massa del satellite.

La forza di attrazione tra satellite e Terra è, invece, data da (Legge di gravitazione universale):

dove  è la massa della Terra, pari a circa  5,972 × 10^24 kg, e G è la costante di gravitazione universale, pari a 6,67×10⁻¹¹ N m²/kg²

Posso dunque scrivere l'equazione:

        (4)

Comparendo il termine m sia al primo che al secondo membro, possiamo semplificarlo dividendo tutto per m. Ecco la prima considerazione: la quota dei satelliti geostazionari non dipende dalla loro massa. Andiamo ora avanti esplicitando la (4) rispetto al termine H, che è la nostra incognita. Dopo qualche passaggio alla fine ottengo:

      (5)

Andando ora a sostituire i valori noti nella (5) ottengo proprio

Così abbiamo risposto anche all'altra domanda. Da notare che la quota a cui orbitano i satelliti geostazionari è circa 5,6 volte il raggio terrestre.

Vi starete chiedendo , a questo punto, quale sarebbe il satellite geostazionario particolare, a cui si fa riferimento nel titolo di questo articolo. E qui arriva il dilettevole.

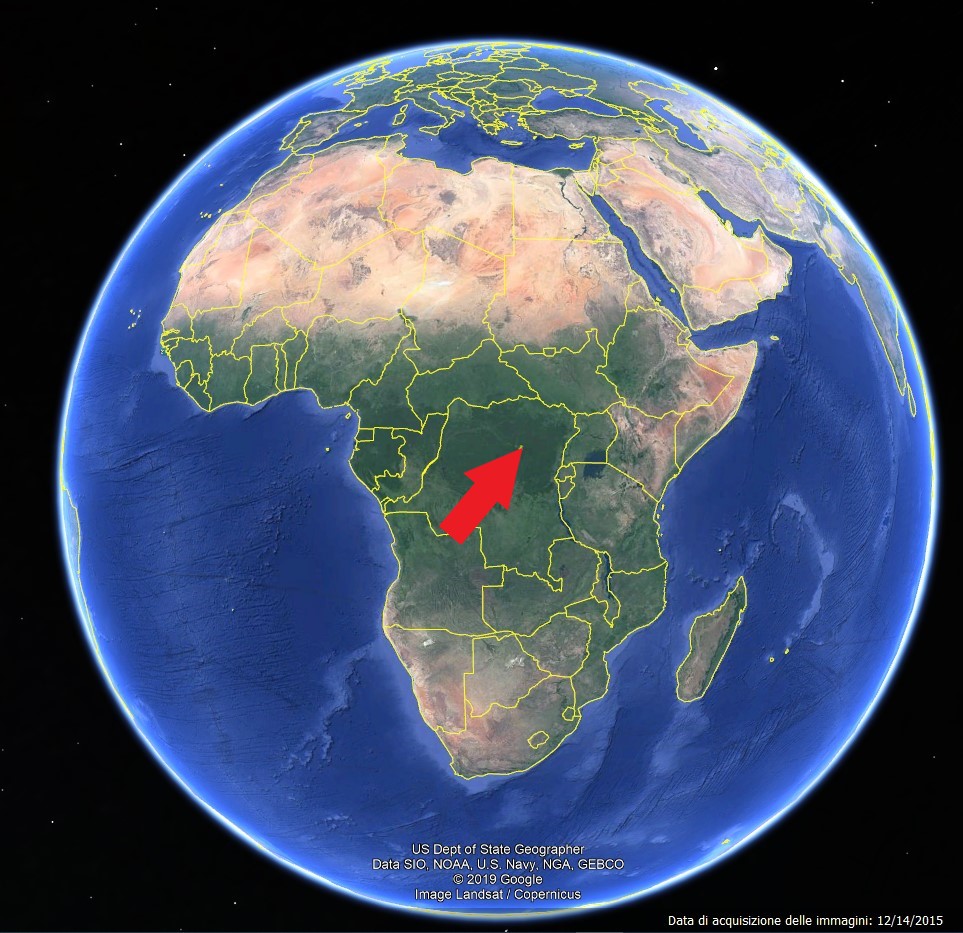
Come molti di voi sapranno già, mi diletto, compatibilmente con il (poco) tempo disponibile, alla pratica del servizio di radioamatore. Le frequenze dello spettro delle onde radio sulle quali, grazie alla loro attribuzione da parte della ITU (International Telecommunications Union), i radioamatori possono effettuare le loro radiocomunicazioni ad uso dilettantistico,  sono tantissime, come numerosi sono i modi e i mezzi di trasmissione. Tra questi, vi è anche un satellite geostazionario di recente messa in orbita, denominato "Oscar-100". Come gli altri satelliti geostazionari, anche Oscar-100 vola a 36000 km di quota rispetto a Terra seguendo un'orbita equatoriale. Esso è fermo (nel senso visto sopra, ossia rispetto agli osservatori terrestri) sulla verticale del Congo, come indicato dalla punta della freccia rossa nelle seguente immagine, tratta da Google Earth:

Grazie alla sua altezza dal suolo, la copertura radio del satellite è notevole, consentendo radiocomunicazioni tra due corrispondenti ubicati, per esempio, uno in India e l'altro in Brasile. La copertura radio è indicata nella seguente immagine.

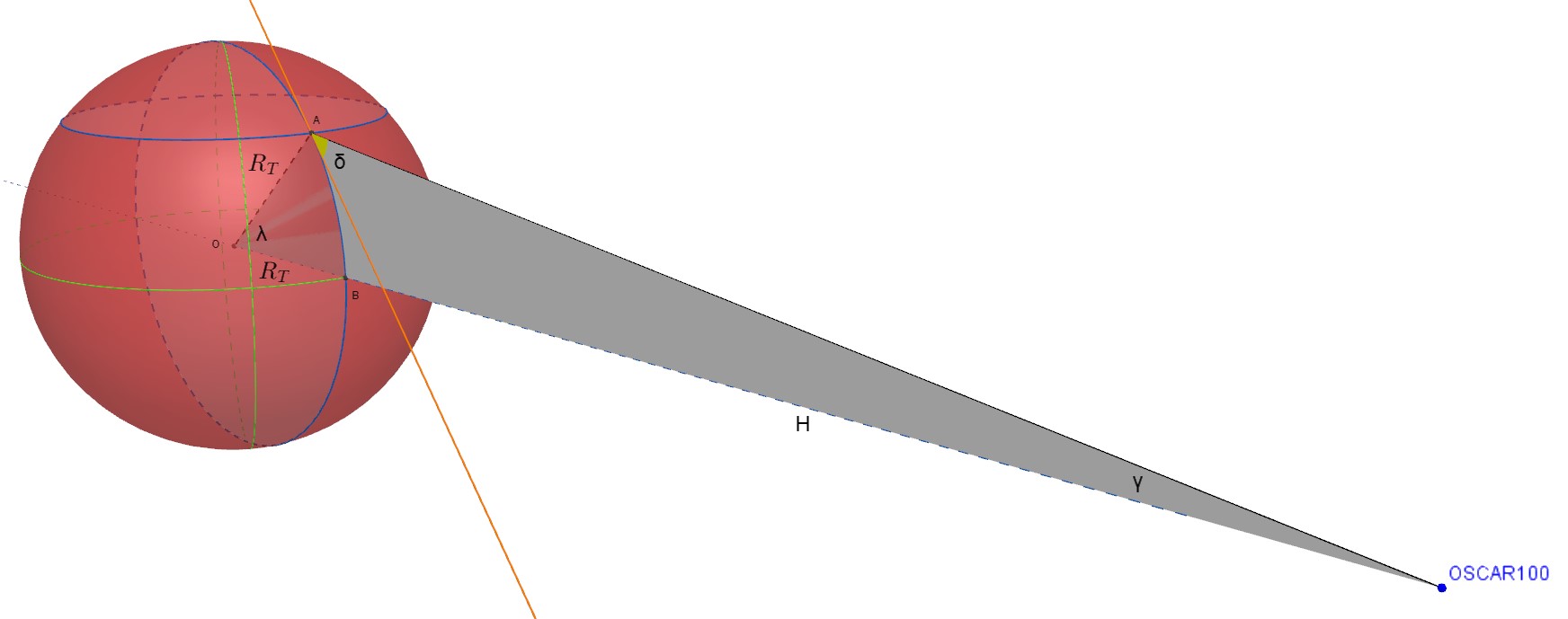
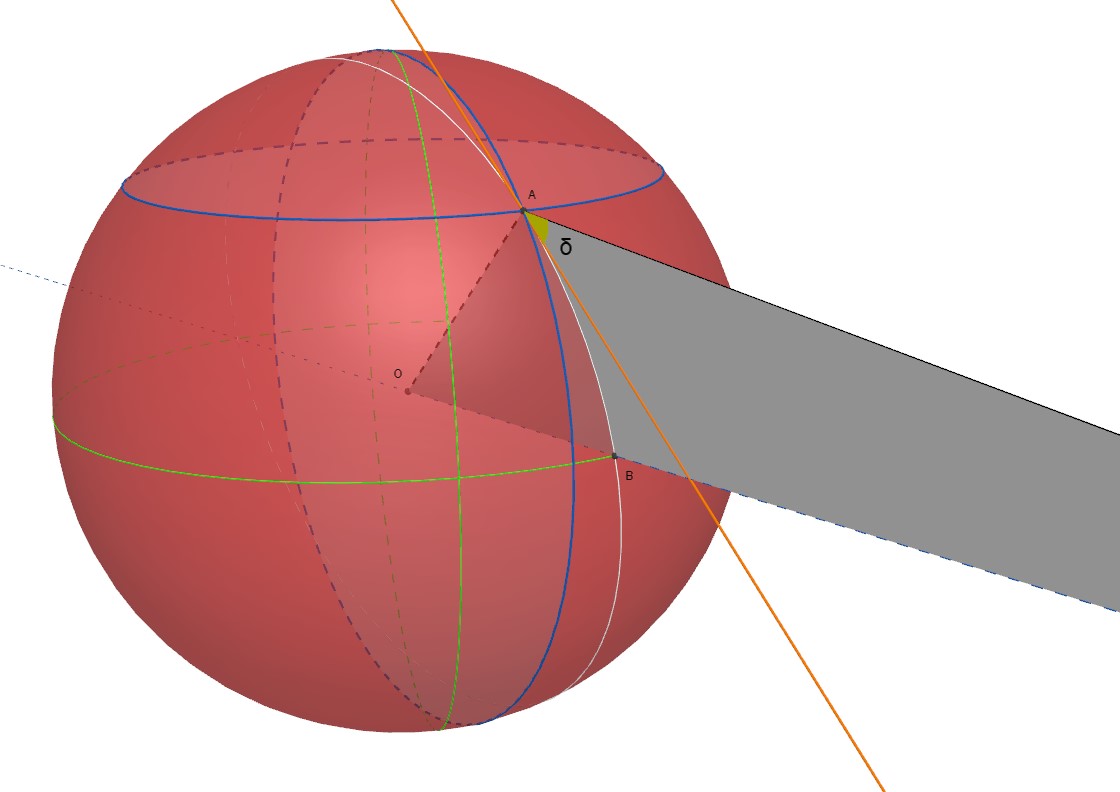
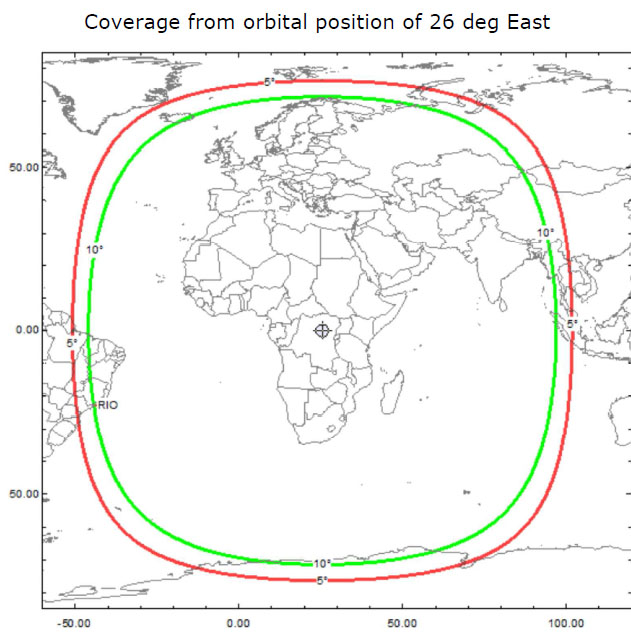 Naturalmente, per poter usufruire delle possibilità offerte da un singolo satellite artificiale per telecomunicazioni, occorre puntargli sopra un'antenna. Nel caso dei satelliti geostazionari la cosa è più immediata, considerato che non occorrono sistemi di inseguimento, visto che il satellite è in questo caso fermo rispetto al suolo. Ma è , comunque, necessario sapere dove puntare l'antenna. Il caso più semplice per ricavare una relazione tra le nostre coordinate geografiche e l'inclinazione e l'azimut da dare all'antenna è quando ci si trova sullo stesso meridiano del satellite. Nel caso di Oscar100 è il meridiano a 25,5° di longitudine Est da Greenwich. E' chiaro che , se ci si trova sullo stesso meridiano del satellite e nell'emisfero Nord, l'azimut dell'antenna, ossia l'angolo orizzontale rispetto al Nord, sarà esattamente di 180°. Basterà, cioè , puntare l'antenna esattamente a Sud. Se ci si trova, invece, nell'emisfero Sud, si dovrà puntarla esattamente a Nord. E l'inclinazione rispetto all'orizzontale ? Ho preparato un modello con geogebra, usufruendo delle sue potenzialità di grafica in 3D. Faccio riferimento alla seguente figura. La sfera visibile in figura rappresenta la Terra. Il punto A indica la nostra posizione geografica sulla superficie terrestre. Il punto B indica la proiezione al suolo del satellite Oscar100. Il punto O rappresenta il centro della Terra.  Le due circonferenze verdi rappresentano l'equatore e il meridiano di Greenwich. Le due circonferenze azzurre, invece, rappresentano il parallelo e il meridiano passanti per la nostra poszione geografica. Considerare il triangolo avente un vertice in O, uno in A e uno nel punto dello spazio in cui si trova il satellite. Considero, inoltre, la retta tangente in A alla superficie terrestre e appartenente al piano meridiano per A (retta arancione in figura). Indico con  l'angolo tra tale retta e la congiungente il punto A con il satellite. In pratica, tale angolo altro non è che quello di inclinazione sull'orizzontale da conferire all'antenna per orientarla verso il satellite. Indico con  la latitudine del punto A e, infine, con  l'angolo tra la congiungente il punto A con il satellite la verticale di quest'ultimo al suolo.

L'angolo  è, evidentemente, dato dalla differenza tra 180° e la somma degli altri due angoli del triangolo, cioè:

Applico al suddetto triangolo il teorema dei seni, per cui posso scrivere:

cioè:

che posso scrivere come:

sviluppando il coseno della somma , semplificando ed esplicitando rispetto a  alla fine ottengo:

Nel mio caso, = 40.060142° , per cui sostituiendo i valori nella suddetta relazione ottengo 43,76°. Questo, però, nell'ipotesi che il meridiano coincida con quello del satellite. Nel caso generale, il procedimento si complica perché il triangolo da considerare non appartiene più al piano meridiano del satellite, come si vede dalla seguente figura, in cui è visibile in bianco il cerchio massimo passante per A e B.

Una volta puntata correttamente l'antenna, la soddisfazione è stata quella di ascoltare il beacon emesso dal satellite in telegrafia Morse. Per questo mi è bastato reperire un minimo di attrezzatura oggi in realtà molto comune: una parabola offset del tipo di quelle usate per SKY, con annesso LNB. L'LNB è l'illuminatore della parabola, che converte il segnale sui 10 GHz proveniente dal satellite ad una frequenza più bassa, sui 740 MHz. Come ricevitore ne ho utilizzato uno digitale che già avevo. Ma basterebbe anche una chiavetta USB SDR.  La chiavetta USB SDR è in pratica un mini-ricevitore digitale in grado di coprire un vasto spettro di frequenze radio. Si trovano oggi in commercio a qualche decina di Euro. Ecco il video che ho effettuato durante il primo ascolto del beacon di Oscar100. Noterete una evidente deriva in frequenza della nota telegrafica. Probabilmente, l'LNB da me utilizzato non era dei migliori.

Il messaggio trasmesso in telegrafia Morse è "HI DE QO100 QRA DK0SB".

Il prossimo passo sarà attrezzarmi anche per la trasmissione, così da poter transitare sul satellite, oltre che ascoltarlo. A quel punto potrei anche ottenere un ulteriore metodo indiretto di misura della velocità delle onde elettromagnetiche nel vuoto. La distanza , tra andata e ritorno del segnale radio tra stazione a terra e satellite è, infatti, notevole, sui 74000 km. Per cui, il tempo impiegato dal segnale radio per andare e tornare comincia ad essere misurabile (circa 1/4 di secondo). Ma di questo parlerò in un successivo articolo.