La volta precedente abbiamo capito il significato della spinta di Archimede e perché deve entrare in ballo il peso del liquido spostato. Ora possiamo tranquillamente arrivare scrivere la formula che lega il peso effettivo del corpo immerso e la spinta di Archimede.

Scriviamo, innanzitutto,  il teorema di Archimede già dimostrato attraverso il suo vero principio. Teniamo, quindi, bene a mente che la formula usata continuamente e ripetuta come una tiritera è il risultato di un qualcosa provato e ben stabilito: non va presa come un dato di fatto.

F_A = -F_Gfl

Ripetiamola ancora, avendo ben presente come è stata determinata

Un corpo immerso nell'acqua riceve una spinta diretta verso l'alto (da cui il segno meno) uguale alla forza peso del fluido spostato. Siamo di fronte a un corpo che ha una certa massa e a una spinta che si preoccupa solo della massa dell'acqua che è stata spostata.

Tralasciamo il segno meno e consideriamo solo i moduli. Scriviamo F_Gfl in modo più esplicativo, dato che compare una forza di gravità (forza peso):

F_A = m_fl g

Notiamo ancora (scusate le ripetizioni) che ciò che compare è la massa del fluido e non certo la massa del corpo immerso.

La densità la fa da padrona

Per l'applicazione ai casi reali di questa eccezionale scoperta conviene avere a che fare con la densità sia del fluido che del corpo immerso. Ci accorgeremo che chi comanda i giochi è proprio la densità che influisce sulla quantità di liquido spostato e quindi sul suo peso e sulla spinta di Archimede. Nessun problema a scrivere la massa in funzione del volume e della densità (supposta, ovviamente costante):

F_A = ρ_fl V_fl g

A questo punto però, trattando con il volume, possiamo tranquillamente inserire il Volume del corpo (Vim) immerso, dato che è esattamente il Volume del liquido spostato, ossia quello che è stato cacciato via dall'entrata del corpo estraneo.

FA = ρ_fl Vim g

Attenzione adesso! Stiamo parlando di volume del corpo IMMERSO, capace di spostare del fluido. Non stiamo parlando del volume di tutto il corpo. Infatti, potrebbe benissimo darsi che non tutto il corpo sia completamente circondato dal fluido. Parliamo solo e soltanto del volume della parte di corpo immersa, la sola che dà origine a una rispettiva spinta di Archimede. Guai, quindi, a pensare al volume (e quindi al peso) dell'intero corpo! La spinta s'interessa solo della parte che entra nel regno del fluido. Proviamo, infatti a mettere una pietra dentro una vaso contenente un fluido. Bene, in questo caso TUTTO il corpo viene immerso (e va a fondo): volume del corpo totale e volume della sua parte immersa coincidono. Proviamo, invece a mettere un pezzo di legno e vedremmo che solo una sua parte sposta acqua, mentre un'altra parte resta al di fuori. Infine, pensiamo a un pallone molto leggero; nessuna parte del pallone disturba l'acqua e la spinta di Archimede è praticamente nulla, Sembra nulla... ma, in realtà, non lo è! Provate infatti a immergere il pallone dentro l'acqua e poi lasciatelo libero, In questo caso la spinta si sente e come! Infatti il pallone viene ricacciato in superficie.

E' giunta l'ora di far entrare il ballo il peso del corpo e vediamo come i tre casi appena descritti siano facilmente comprensibili attraverso formule estremamente banali.

 

Tre casi e due sotto casi

Se il peso del corpo immerso è quello di TUTTO il corpo, la sua forza peso è data da:

F_GC = m_C g                 (m_C è la massa di tutto il corpo, F_GC è la forza peso di tutto il corpo)

scriviamo anche questa forza mettendo in evidenza volume e densità del corpo

F_GC = V_C ρ_C g

Immergendo il corpo in acqua assistiamo alla lotta tra le due forze: quella peso del corpo e la spinta di Archimede che reagisce all'ingresso dell'intruso. In tutti i casi si deve raggiungere un equilibrio finale.

I tre casi precedenti si riferiscono alle tre possibilità:

F_GC > F_A

F_GC = F_A

F_GC < F_A

 

a) F_GC > F_A

In questo caso abbiamo:

V_C ρ_C g > ρ_fl V_fl g

l'accelerazione g si semplifica e otteniamo:

V_C ρ_C > ρ_fl V_fl

ρ_C /ρ_fl > V_fl /VC

Vediamo  che il corpo va a fondo: la spinta verso l'alto non riesce a equilibrare il peso del corpo.

Ne segue che il volume spostato è proprio il volume del corpo, ossia V_fl =V_C , da cui;

ρ_C /ρ_fl > 1

ρ_C  > ρ_fl

Se la forza peso è maggiore della spinta di Archimede, il corpo affonda in quanto la spinta è sempre minore del peso totale del corpo. Perché questo succeda è necessario che la densità del corpo sia maggiore di quella del fluido. L'equilibrio è raggiunto solo sul fondo, quando lo stesso fondo si oppone alla gravità del corpo. Questo caso lo vediamo nella prima parte a sinistra della Fig. 3

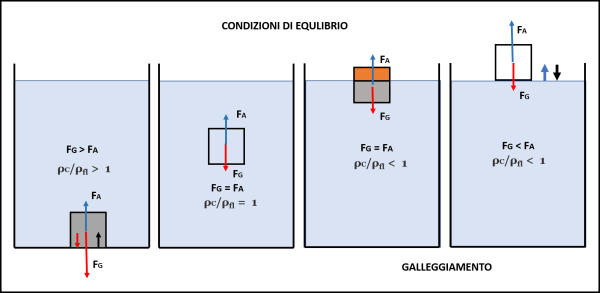
b) F_GC = F_A

Passiamo al caso limite, ma estremamente interessante, in cui la forza peso eguagli perfettamente la spinta. Questo caso si divide in due sottocasi:

(1b) Il corpo si immerge completamente ma non va a fondo. Per esservi una spinta è necessario che vi sia un volume sommerso, altrimenti non si origina la spinta di Archimede. Tuttavia, iniziando a immergersi, il corpo riceve una spinta nettamente più piccola del proprio peso. L'equilibrio si ottiene solo quando tutto il corpo è immerso, dato che sappiamo che la spinta di Archimede è esattamente uguale al peso del corpo. In qualsiasi posizione venga messo dentro al fluido  si ha l'equilibrio;

(2b) Il corpo comincia ad affondare e poi si ferma senza essere entrato completamente nel fluido. All'inizio , il volume spostato genera una spinta che non riesce a controbilanciare il peso totale del corpo: il corpo si immerge. Giunti a una certa profondità, il volume sommerso è sufficiente a generare una spinta uguale e contraria al peso del corpo e si raggiunge l'equilibrio.

In entrambi i sottocasi abbiamo

V_C ρ_C g = ρ_fl V_fl g

V_C ρ_C = ρ_fl V_fl

Nel sottocaso (1) il corpo è completamente sommerso, per cui abbiamo nuovamente V_C = Vfl, ossia:

ρ_C = ρ_fl 

Perché capiti questo caso (non comune) è necessario che le due densità siano esattamente uguali. In pratica è come se avessimo immerso nell'acqua un corpo fatto di... acqua.

Nel sottocaso (2) il corpo non è completamente immerso, per cui esiste una differenza tra Vfl e V_C. Per l'esattezza

V_C > V_fl

ρ_C/ρ_fl = V_fl /V_C < 1

ρ_C < ρ_fl 

La densità del corpo è minore di quella del fluido. Il corpo galleggia con solo una parte immersa. In pratica è sufficiente la spinta dovuta a una parte del volume del corpo per ottenere l'equilibrio.

I due sottocasi sono riportati nella seconda e terza parte della Fig 3.

c) F_GC < F_A

Nel terzo caso  abbiamo

V_C ρ_C g < ρ_fl V_fl g

In  questo caso il corpo si rifiuta di immergersi, dato che basterebbe solo un piccolo volume di fluido spostato per rompere l'equilibrio. Qualsiasi parte sommersa sarebbe sufficiente a generare una spinta verso l'alto maggiore del peso del corpo. Basta pensare a cosa succederebbe  se  immergessimo completamente il corpo nel fluido:  lasciandolo libero la spinta di Archimede sarebbe sempre maggiore del peso del corpo. I due volumi sono giocoforza uguali perché costretti ad esserlo, per cui V_fl = V_C, ma immediatamente la spinta di Archimede prende il sopravvento e spinge senza problemi verso l'alto (è maggiore della forza peso). Ne risulta nuovamente che

ρC < ρ_fl 

Per raggiungere l'equilibrio il corpo si solleva fino al pelo dell'acqua. Anzi, ne uscirebbe anche fuori con violenza e volerebbe in cielo se il suo peso (ben maggiore di quello dell'aria spostata) non lo riportasse a contatto con l'acqua.  Un pallone da spiaggia si adagia sull'acqua così come una pietra si ferma sul fondo.

Possiamo concludere che sia nel sottocaso (2) che nel terzo caso è necessario che la densità del fluido sia maggiore di quella del corpo. Entrambi in casi rientrano nel fenomeno del galleggiamento che merita di essere studiato in dettaglio. I parametri critici per dividere i risultati risultano le densità, e possiamo ricapitolare i risultati ottenuti:

i) se la densità del corpo è maggiore di quella del fluido, il corpo va a fondo.

ii) se la densità del corpo è uguale a quella del fluido il corpo si immerge completamente, ma resta in equilibrio

iii) se la densità del corpo è minore di quella del fluido il corpo galleggia, ma può rimanere sia parzialmente immerso o del tutto al di fuori del fluido.  Quando rimane una parte sommersa, vuol solo dire che si è raggiunto l'equilibrio, ossia la parte sommersa è sufficiente a creare una spinta che è uguale al peso di tutto il corpo.

 

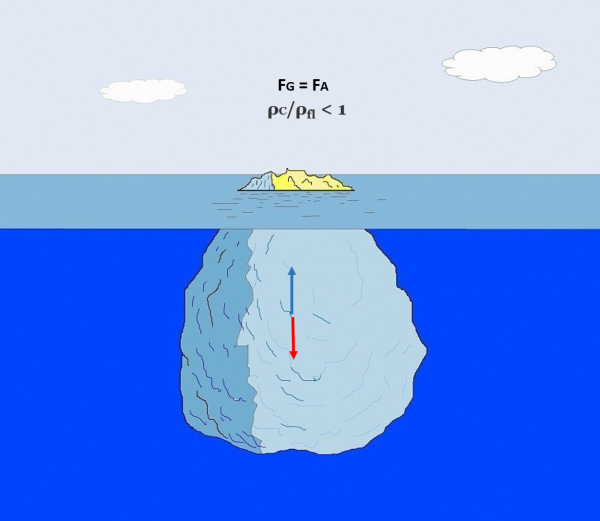
Un esempio famoso: l'equilibrio di un iceberg

L'iceberg è in equilibrio per cui vuol dire che è stata raggiunta l'uguaglianza tra il suo peso e la spinta di Archimede. Ossia possiamo scrivere;

ρ_ice V_ice =  ρacq V_acq

Dove V_ice è il volume di tutto l'iceberg e V_acq è il volume immerso nell'acqua.

noi sappiamo che il ghiaccio ha una densità minore dell'acqua salata. In particolare:

ρacq = 1.02 g/cm³

ρ_ice= 0.92 g/cm³

Si ha questo valore più basso, dato che le molecole si combinano tra loro in disposizione meno efficiente. Possiamo, allora scrivere:

V_acq= ρ_iceV_ice/ρacq  = V_ice 0.92/1.02 = 0.90 V_ice

Questo dimostra che la parte sommersa dell'iceberg è pari al 90% del volume totale. Ecco perché si dice: "E' solo la punta di un iceberg". Fuori sembra un ghiacciolo, ma sotto c'è ben altro. Il Titanic insegna... In altre parole, per ottenere l'equilibrio è necessario che la spinta si Archimede abbia a disposizione il 90% del volume dell'intero corpo.

 

La prossima volta passeremo ad analizzare più a fondo  il galleggiamento, dove scopriremo che la densità permette anche configurazioni di equilibrio meno prevedibili.

 

Gli altri articoli dedicati al Teorema di Archimede li trovate QUI