Categorie: Matematica
Tags: geometria quiz somma angoli trigonometria
Scritto da: Vincenzo Zappalà
Commenti:34
Quiz: sommiamo gli angoli **/****
Un doppio quiz, a due livelli. La prima parte si può risolvere in moltissimi modi. Un prestigioso regalo a chi darà la risposta più "elegante" (a mio giudizio, ovviamente!).
PRIMA PARTE **
Eccovi una somma di angoli che può determinarsi con almeno 54 procedimenti. Escludiamo a priori tutti quelli che fanno uso della trigonometria. Chi riesce a trovare il più "elegante"? Ovviamente, l'eleganza la deciderò io: è o non è un Circolo DEMOCRATICO!!!!
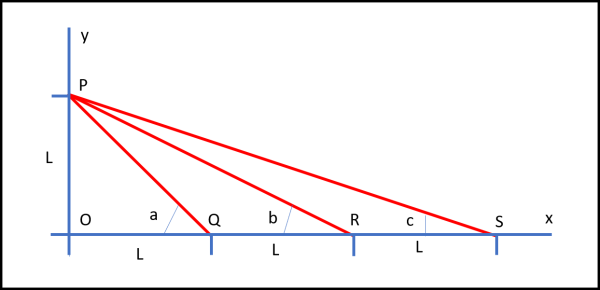
La figura che segue illustra il problema.
Da un punto P, posto a una certa altezza L sull'asse delle ordinate, tracciamo la congiungente con un punto posto sull'asse delle x, tale che xQ = L. Poi facciamo lo stesso con un punto R posto sull'asse x, con xR = 2L. Infine, ripetiamo l'azione per un punto S posto sull'asse x, tale che xS = 3L.
Le tre congiungenti (PQ,PR,PS) formano gli angoli a, b e c , rispettivamente, con l'asse delle x.
Quanto vale la somma a + b + c ?
SECONDA PARTE ****
Complichiamo un po' il problema.
Non fermiamoci a S e andiamo avanti fino a nL con n grande come volete ... cosa succederà della somma degli angoli? A questo punto, la trigonometria è d'obbligo...
Si riuscirà ad arrivare a 360°?
In questo caso usate pure il metodo che volete... più rigoroso è e meglio è!
Soluzione QUI






34 commenti
Caro Enzo, a parte che il modo più elegante, oggettivamente, è il goniometro.... che so esserti inviso, si può ripiegare su questa soluzione
prima di tutto a= 45° poi a+x+b = a+y+c = 90° da cui x+b = y+c
quindi x= c e y=b
Risposta: a+b+c = 90°
Per la seconda risposta, quella che richiede una soluzione tri-goniometrica, lascio spazio agli altri lettori.
Ciao.
Caro Oreste,
potresti spiegarmi come ottieni x = c e y = b a partire da x + b = y + c ?
Io vedo solo che
x + b = 45
y + c = 45
Che ha, ad esempio, la soluzione:
x = 20 e b = 25
y = 30 e c = 15
oppure
x = 23 e b = 22
y = 28 e c = 17
ecc., ecc.
Guarda questa figura ...
I due triangoli PRO e PST sono simili : sono triangoli rettangoli con cateti che stanno nel rapporto 1:2
Conseguentemente l'angolo y e l'angolo b sono uguali. etc...
riscusa, ma per quale motivo il cateto OP dovrebbe essere la metà di PT ?
Sarebbe bene spiegare ogni singolo passaggio, dato che la prima parte è un quiz con due soli asterischi...
Non so se la figura è fatta bene o solo approssimativa, ma -al limite- direi che PT è la diagonale e PO è il lato di un quadrato. Il loro rapporto non è 2:1... Se invece non sono quadrati come hai costruito PT?
Nel triangolo rettangolo PRO:
Cateto PO = lato quadrato ( L)
Cateto OR = 2 volte lato quadrato ( 2L)
PO vale 1/2 di OR
Il rapporto tra i cateti è di 1 a 2
Nel triangolo rettangolo PST:
Cateto PT = una diagonale del quadrato
Cateto TS = due diagonali del quadrato
PT vale 1/2 di TS
Il rapporto tra i cateti è di uno a due.
In ambedue i triangoli rettangoli il rapporto tra i cateti è di 1 a 2
Se è consentito l'uso di un compasso e un righello, mi è venuta in mente la costruzione in figura:
In pratica, costruisco il successivo triangolo sull'ipotenusa di quello precedente. Così facendo ottengo che alla fine la somma dei tre angoli è visivamente pari a 90 gradi.
Per Oreste;
Mi manca solo la dimostrazione che, dato che b = y, la somma è uguale a 90°...
Sforzati un po' e non pensare solo alle ... castagne!
Per Arturo:
preferirei qualcosa di meno "tecnico" e più teorico...
Ricordati sempre che ti aspettiamo per il tronco di Archimede!
Ah... ho capito Pautasso l'ermetico... La seconda dimostrazione voleva solo convalidare la prima dimostrazione. mmmmh... un po' troppo contorta, si può fare meglio...
Ripropongo la figura del primo commento...
Assodato che b=y, per la proprietà simmetrica della uguaglianza abbiamo che y=b
Ora, come accennato in figura ( nel terzo quadrato a destra ) , sostituiamo la b alla y, e otteniamo che c+b+a = 90°
Infine, per la proprietà commutativa della addizione (cambiando l'ordine degli addendi il risultato non cambia), possiamo dire che a+b+c = 90°.
Passiamo ad altro.
Da quando la raccolta del tartufo non è consentita (come sai il divieto è scattato il 31 gennaio) Arley ha molto tempo libero e, tra un sudoku diabolico e una partita di scacchi contro il computer, ha sbirciato anche il quiz e non ha mancato di dire la sua sulla seconda parte.
Secondo lui occorre calcolare la somma di una serie di termini del tipo arctan(1/x) con x da 1 a infinito (possibilmente).
Dice che la sequenza degli argomenti (1/x) è una serie armonica ed è divergente, questo significa che la sua somma tende a infinito (sostiene di aver visto altri quiz in cui se ne parla).
Congettura che la somma dei corrispondenti valori della funzione arctan(1/x) tende anche essa all'infinito* quindi il suo valore supererà certamente i 360°.
* Arley lascia ad altri ( escluso me) la necessaria dimostrazione rigorosa; fa solo notare che al crescere di x, la tangente decresce e tanto più decresce, tanto più tende a coincidere con l'arco. Conseguentemente ipotizza che arctang(1/x) tende progressivamente a valere 1/x al crescere di x.
)

Ti ho riferito pari pari le sue parole; chissà se nella sua canina follia ...
Mi ha comunque raccomandato di allegare la sua foto in segno di saluto per te ed il pubblico dei lettori, cosa che faccio con piacere.
Checché tu dica (ma siamo sicuri che se a = b anche b =a ?) il metodo (finalmente spiegato in modo divulgativo) si può migliorare in ... eleganza.
Per la seconda parte i 4 asterischi indicano che sarebbe bene dare una soluzione meno approssimativa.
Naturalmente, la costruzione tecnica poggia sempre su solide basi teoriche..

Ecco la versione con geogebra
Una volta effettutata la rototraslazione dei triangoli POR e POS in maniera tale che la base del triangolo successivo poggi sull'ipotenusa di quello precedente, come in figura, si dimostra subito che l'angolo a+b+c è di 90°. Infatti, se chiamo con x l'angolo QPS, considerando che l'angolo PQS è pari a b+c+90°, vale la relazione:
x+(b+c+90)+c=180 (somma angoli interni di un triangolo)
Ma è anche:
x=90-(a+c)
mettendo assieme le due relazioni ottengo:
b+c=a
cioè, essendo "a" banalmente pari a 45°:
b+c=45°
Quindi l'angolo a+b+c=90°
ops.. mi rendo conto che i passaggi successivi alla figura con geogebra sono conseuenza della costruzione stessa (comunque esatta). In effetti, è quest'ultima che contiene già al suo interno la risposta, perché la retta tratteggiata passante per Q va a intercettare l'asse y esattamente nel punto di ordinata 3L . Da lì tutto il resto viene di conseguenza.
sì, sì... ma perché l'angolo in Q vale 90° gradi? Tutto deriva da lì... Perché l'ipotenusa più lunga, una volta ruotata, deve essere perpendicolare alla retta orizzontale? Chi me lo dice? Il fatto che viene così ruotando è una dimostrazione che mi piace poco...
Forza Oreste e Arturo, ci sono altri 52 procedimenti...!!!
e poi mi raccomando la seconda parte... e il tronco di sezione quadrata... lì puoi divertirti un sacco con geogebra...
Tempo e lavoro tiranni, caro Enzone...
Al volo, per la seconda parte, entrano in gioco le serie. In particolare la serie arcotangente
(considerando il generico triangolo :) da cui
da cui =\frac{L}{nL}=\frac{1}{n}) quindi
quindi 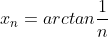 )
)
Tale serie, nonostante il limite di arctan (1/x) sia zero al tendere di x all'infinito, diverge per n tendente all'infinito. Quindi, la somma degli angoli supererà sicuramente 360°
va bene, va bene... io scherzo. Capisco i problemi dei "giovani"!!!!
Poi spiegherò perché diverge...
Sarà più elegante ?
Introduco i punti T U V
il segmento QT vale L/2 come si vede nella figura. Il segmento TU è perpendicolare alla diagonale VR.
Osserviamo il triangolo rettangolo TUR :
il cateto TU ha lunghezza identica a VU e qundi pari a 1/4 della diagonale VR ;
il cateto RU ha lunghezza pari a 3/4 della diagonale VR il rapporto tra i cateti è 1 a 3.
Anche il rapporto tra i cateti del triangolo POS è di 1 a 3, per costruzione.
Quindi l'angolo x è identico all'angolo c e ( in prossimità del punto R ) invece di b+x+a posso scrivere b+c+a, o se preferite a+b+c=90°
Non male... già meglio
E quest'altra?
Chiamo T l'intersezione tra PS e la diagonale RU. Per costruzione T è il centro del quadrato.
Nel triangolo rettangolo PQT, il cateto QT è lungo metà diagonale. L'altro cateto QP è lungo il doppio (è una diagonale).
Il rapporto QT/QP vale 1/2 . Anche nel triangolo rettangolo POR , il rapporto PO/OR vale 1/2. Sono triangoli simili.
Ne deriva che l'angolo TPQ, ha lo stesso valore dell'angolo PRO, ossia vale b.
Nel triangolo rettangolo isoscele POQ , l'angolo OPQ ha lo stesso valore dell'angolo PQO, ossia vale a.
I due triangoli UPT e RST sono congruenti: l'angolo TPU , ha lo stesso valore dell'angolo TSR, ossia vale c.
In conclusione a+b+c = 90°
Troppi rapporti... troppi rapporti. Qualcosa di più sbrigativo...
Li vuoi provare tutti e 54 ????
Siamo sempre intorno all'otto e vorrei dare almeno un bel NOVE!
Secondo me sono più di 54. Te ne deve essere sfuggito qualcuno.
Hai contato anche il migliore di tutti (quello con il goniometro)??
Con il goniometro è 10 e lode.
il goniometro... che schifezza TECNOLOGICA, proprio da ingegneri...
E poi con il goniometro non troverai mai 90.0000000, ma 89.9 o 90.1 .... se proprio sei bravo!
Guarda.... questa è l'ultima poi ti arrangi.
Il punto T è al centro del quadrato. I triangoli PQU e UTR sono simili. PQ = 2TR e QU=2TU
TU vale quindi 1/3 di QT, vale a dire di TR pertanto l'angolo TRU vale c
a+b+c = 90° (proprio come con il goniometro,...per chi lo sa usare bene)
Se non ti va bene ti faccio mordere da Arley.
bello... 8 + !
E questo, con gli angoli alterni interni ? Neppure questo ? ... Ciao.
La similitudine di TQP e POR non è spiegata. Un metodo ingannevole per ridurre i passaggi...
E poi tieni presente che, in regime democratico, la scelta del boss vale sempre un punto in più di ogni altra scelta, per definizione .
.
E se ti chiedessi che NON voglio triangoli simili, ma solo uguali (al limite). Dai che ce la puoi fare...
Per ringraziare della indiscrezione, ti dedico questa poesiola....
Goniometro: istruzioni per l'uso
All'amico Professore / Il goniometro fa orrore
Ma ho capito la ragione / di codesta preclusione
Un preciso risultato / Va con calma elaborato:
Se ripeti la misura / E la media fai con cura,
Troverai per tuo diletto / Un valor proprio perfetto.
Tu misura volte mille... / Risultati da scintille
E se superi il milone / Sfiorerai la perfezione.
Se misure ne fai una, / Garanzia non hai alcuna.
Via, non essere testardo / Osa andar oltre al miliardo.
Beh... sono commosso da tale spirito lirico. Va bene ti meriti un 9 ----. Ma... chi ce l'ha il tempo per fare un miliardo di misure????? Oreste, pensa agli alberi di castagne e sollevane uno in modo da ottenere un triangolo isoscele di grande... eleganza!
Grazie Enzo, penso di avere capito il tuo suggerimento (dico...penso) ma non voglio toglierti la soddisfazione di presentare l'elegante triangolo isoscele nella soluzione al quiz.
Piuttosto, mentre ero sulla pianta, (Mau voleva farmi scendere ma ho fatto finta di non vederlo e non sentirlo) mi è venuta questa idea un po' pazza, che ti spiego in un battibaleno.
Formulo il problema nel seguente modo.
Disegno tre triangoli con i rapporti tra i cateti 1:1 1:2 1:3 affiancando i loro angoli acuti e valuto il valore della somma complessiva.
Ecco come si presenta il relativo disegno.
Al centro il triangolo giallo con rapporto 1:1 tra i cateti e il suo bell'angolo a
A sinistra il triangolo rosso: rapporto 1:2 e angolo b
A destra il triangolo verde: rapporto 1:3 (l'unità di misura è la diagonale) e angolo c
La somma a+b+c vale 90° per il seguente motivo:
I due triangoli neri hanno lo stesso rapporto 1:2 tra i cateti e sono perpendicolari. quindi anche le loro ipotenuse sono perpendicolari e tra esse è contenuto l'angolo a+b+c.
Non so quanto sia elegante questa soluzione, forse si potrebbe migliorare usando colori diversi, a seconda dei gusti.
P.S.
Dire che due triangoli sono perpendicolari è una licenza poetica per dire che il cateto maggiore dell'uno è perpendicolare al cateto maggiore dell'altro e analogamente per i cateti minori.
Non male, non male, ma sempre... rapporti. Di questi tempi, però, è meglio non avere rapporti troppo stretti!
In effetti devo convenire che 1:2 è già un rapporto un tantino disinvolto e 1:3 è decisamente disinibito...
Caro Enzo, in attesa della spiegazione che nel tuo commento hai preannunciato, riguardo al motivo per cui la serie arctan(1/x) diverge, propongo questo ragionamento "fai da te".
Diamo per acquisito il fatto che la somma della serie armonica è divergente.
La funzione arctan(1/x) rappresenta la lunghezza dell' arco la cui tangente vale 1/x.
Nella situazione iniziale x=1 , la tangente vale 1 , l'angolo è di 45° e l'arco vale 3,14/4
Al crescere di x l'arco si mantiene sempre più piccolo della corrispondente tangente ma tende progressivamente ad assumere il suo stesso valore.
Mettiamoci nel caso più sfavorevole, ignorando questa tendenza, e diciamo che per qualsiasi x l'arco vale 3,14/4 volte la tangente. Valutiamo quindi la serie di (3,14/4 * 1/x) per i valori da 1 a infinito.
Il valore della somma di questa serie sarà: 3,14/4 * il valore della somma della serie armonica (che è infinito).
Visto che questa serie è divergente, a maggior ragione lo sarà anche la serie arctan (1/x).