Categorie: Matematica Storia della Scienza
Tags: geometria mostro marino quiz supereroi
Scritto da: Vincenzo Zappalà
Commenti:21
il mostro eroico **/****
In pieno oceano appare un mostro marino dall'aspetto terrificante. La Scienza non può che analizzare attentamente l'unica fotografia scattata, dalla quale ricava uno schema di massima delle dimensioni e della forma... Chi è che può aiutarci per correre ai ripari?
La foto del mostro lascia tutti sbalorditi, sia per l'aspetto che per le dimensioni veramente fuori dal comune. Per il momento non ha ancora assalito nessuna nave, ma ormai non si parla che di lui e la paura serpeggia tra tutti i marinai.
PRIMA PARTE **
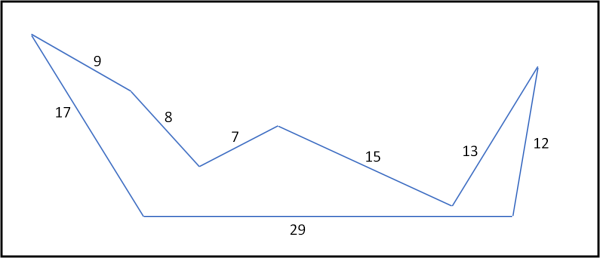
Dalla foto è stato ricavato uno schema geometrico, molto "spigoloso", del mostro (sperando che non sia "spigoloso " anche il suo carattere!)
Le parti sono state tutte approssimate a un numero intero e quindi chi vuole aiutare la Scienza a descrivere la forma e le dimensioni sappia che ogni segmento "importante" deve risultare un numero intero (se non lo è esattamente la colpa è del disegno e bisogna arrotondarlo al numero intero più vicino).
N.B.: Questa volta ho controllato e ricontrollato i vari segmenti e direi che non ci dovrebbero essere incertezze. Fate solo molta attenzione e al limite fate presente i problemi che incontrate. Se legati allo svolgimento esatto arriverò in vostro soccorso.
La prima domanda, per facilitare -anche se non sembra- la seconda parte, è: Quanto vale la superficie dell'intero mostro proiettata sul piano del disegno.
SECONDA PARTE ****
Poi inizia la seconda fase, quella di contrattacco. In qualche modo si deve rendere inoffensivo il cetaceo o quello che è. Nessuno se la sente, però, di scendere in battaglia aperta. Si decide, perciò, di affidarsi ai soliti supereroi . In particolare ai cinque che sono rimasti sulla Terra (gli altri stanno compiendo imprese eccezionali oltre i Bastioni di Orione): Il loro capo indiscusso è Superhero, forse il più dotato di tutti, il vero rappresentante del gruppo dei salvatori della Terra. Però, però... malgrado si cerchino dappertutto, non rispondono ai richiami. Dove sono finiti, accidenti! Aiutatemi a ritrovarli, gli Oceani sono -forse- in grave pericolo.
Lo so, lo so, la presentazione è veramente assurda e quasi incomprensibile. Tuttavia, abbiamo tanto tempo e possiamo dedicarci anche a queste "apparenti" stupidaggini. A parte il quiz in se stesso, il racconto ci serve per introdurre qualcosa di storicamente molto importante...
N.B.: I quattro asterischi sono stati attribuiti per la difficoltà di trovare la chiave di volta del quesito e non per la complessità di tipo matematico o geometrico, veramente irrisoria.
QUI la risposta alla prima domanda
QUI la risposta alla seconda domanda







21 commenti
sarà mica una cosa così?
Oppure così ...?
chiedo scusa a tutti... ma mi sono fidato troppo della precisione del PPT. Le distanze risultano leggermente sbagliate. Preferisco inserire io i valori dei lati esterni. Il quiz cambia decisamente la prima parte e si facilita in un poco ...
BLOCCATE TUTTO.... DOMANI LO METTO A POSTO!!!
Interpreto la richiesta come un problema di trasformazione della sagoma articolata in un rettangolo, molto più docile per calcolarne l'area.
La conversione della forma irregolare in quella del rettangolo si realizza con una semplice integrazione grafica, la cui precisione dipende dalla accuratezza della costruzione.
Questa figura illustra appunto come procedere qualitativamente per ottenere l'area equivalente.
Naturalmente potrei essere totalmente fuori strada ....
Interessante... potresti, però, illustrare meglio il procedimento usato per giungere a un rettangolo? Dove saltano fuori il 10 e il 17.5? Cerchiamo di spiegare sempre le cose con la massima semplicità e chiarezza (se possibile).
Inizio illustrando la trasformazione di un trapezio in un rettangolo di base arbitraria.
Il trapezio blu ha lati ABCD. Proietto il punto medio di AB , ossia M sull'asse Y e trovo M'.
Fisso un punto P a distanza arbitraria dall'origine assi O. PO è la base "b".
Unisco P a M' e dal punto base D traccio la parallela a PM fino ad incontrare la verticale per C nel punto H.
Infine proietto H sull'asse Y. trovando l'altezza h del rettangolo rosa di base b.
L'area di tale rettangolo è uguale a quella del trapezio.
Infatti, dalla similitudine dei due triangoli POM' e DCH (rettangoli e con ipotenuse parallele) consegue che
PO: DC = OM':CH quindi
PO*CH = DC*OM' ma PO= b CH=h e OM'=OM= (AD+BC):2
b*h = DC* (AD+BC)/2
area rettangolo = area trapezio
A questo punto basta suddividere la mostruosa spezzata del dorso in 5 trapezi e la mostruosa spezzata del ventre in 3 trapezi. (quello centrale ha area nulla)
Scelta la base arbitraria (ad esempio quel 10 che ho scritto), basta procedere accumulando i contributi dei 5 trapezi sopra e trovare la altezza complessiva corrispondente. Altrettanto si farà per i contributi cumulati dei 3 trapezi di sotto , trovando la altezza ad essi corrispondente. Il rettangolo determinato dalla base e dalla differenza delle due altezze ha la stessa area del mostro. Abbiamo così la quadratura , anzi la rettangolatura del mostro.
Il valore di 17,5 l'ho semplicemente trovato contando i quadretti (si puo?)
Precisazione: i tre "trapezi" di base, essendo la pancia del mostro appoggiata sul pelo libero della superficie marina, (ossia l'asse x) diventano semplicemente due triangoli e un segmento intermedio, ma il ragionamento non cambia.
Giuro che continuo a seguirti poco... quali sono i trapezi? e poi come contare gli spazi vuoti dei trapezi?
In ogni modo l'area totale (che dovrebbe essere secondo te 175) non è esatta. La differenza è troppo grande per essere dovuta a errori di misurazione... (ho provato anche io e resto sempre nei limiti più che accettabili). Inoltre, anche ad occhio un rettangolo di base 17.5 e altezza 10 è decisamente più piccolo del mostro...
Ricontrollo la costruzione che ti spiegherò con maggiori dettagli domani.
Vedo comunque che hai aggiunto due valori che non erano presenti nel testo del quiz, ossia un 6 a sinistra e un 5 a destra. Immagino che se ne debba tenere conto.
Separo le due integrazioni grafiche.
Ecco la prima, relativa ai 5 segmenti superiori. I 5 trapezi sono T1 T2 T3 T4 T5.
Fissata la base di integrazione, fornisce l'altezza del rettangolo la cui area corrisponde all'area sottesa tra i 5 segmenti e l'asse x.
Segue la seconda costruzione che opera sul profilo dei tre segmenti inferiori e trova la area del rettangolo (di base b) equivalente alla somma sottostante ai 3 segmenti (quello centrale è adagiato sull'asse ). si tratta di due triangoli rettangoli a inizio e fine della spezzata la cui area complessiva andrà sottratta a quella dei 5 trapezi
Ecco la figura:
Nel tracciare le linee costruttive occorre essere precisi con parallelismi e intersezioni. La qualità del risultato dipende esclusivamente da questo.
Non so quanto l'area trovata (192 unità al quadrato), sia lontana dal risultato atteso, comunque il metodo grafico è basato su un principio abbastanza semplice e geometricamente giustificato.
Per un calcolo "aritmetico" occorrerebbe trovare i valori di due segmenti x e y nella figura.
Basterebbe applicare il teorema di Erone (che fornisce l'area del triangolo, noti i suoi lati) , ai 5 triangoli di lati:
9 17 x
6 8 x
6 7 y
29 (15+5) y
5 13 12
Basta, lascio spazio agli altri lettori.
Ops... ho aggiunto i due valori senza volerlo. Va beh... un aiuto in più (a parte che si potevano ricavare con una squadretta). Posso dirti che adesso le cose vanno meglio... 192 è tutta un'altra cosa rispetto al 175, non ti pare? Continuo a trovare farraginoso il metodo dei trapezi, quando puoi misurare liberamente tutti i segmenti che vuoi...
Mi spiace che, comunque, nessuno si sia ancora ricordato di questo articolo...
http://www.infinitoteatrodelcosmo.it/2019/12/29/sezioniamo-un-poligono-seguendo-wallace-bolyai-gerwien/
Anzi... visto che era caduto nei giorni di Natale, ho deciso di riproporlo in legame più o meno stretto con il mostro eroico. Se non altro è un passatempo per bambini un po' cresciuti e genitori annoiati...
Pur non ricordando l'articolo ( anche se lo avevo letto) , l'idea del tangram mi era venuta, ma l'ho accantonata subito, perché avevo interpretato la richiesta come la ricerca di una costruzione che consentisse solo una o. al massimo due misure, quindi la ricerca di un rettangolo equivalente.
Mantengo la promessa di non aggiungere altro.
L'importante era sì trovare l'area, ma anche prepararsi per la parte più ... difficile!
Ho fatto tanta fatica a fare il disegno proprio per essere in grado di CREDERE nelle misure.
beh?! Vi siete fermati proprio sul più bello? Mi meraviglio Mau & co.
Non so chi sia questo "co.", ma io avevo scritto negli ultimi 2 commenti
Prima: Basta, lascio spazio agli altri lettori.
E poi: Mantengo la promessa di non aggiungere altro.
ma io, invece, ti sto spronando... il co è ovviamente Pautasso, visto che non si muove nessun altro!|
Comunque, va bene così... se non rispondono entro domani, darò la risposta e non gettatemi le pietre!
Il disegno BUONO è quello dell'articolo non quello dei commenti... mamma che caos che ho fatto... abbiate pazienza!
In realtà ieri sera ci siamo scambiati due idee con Oreste (tenendoci a distanza di più di 4 metri) sul fatto che i due disegni fossero leggermente diversi e avevamo fatto questa sovrapposizione che lo metteva in evidenza.
Poi abbiamo deciso di non chiederti chiarimenti perché alla fine l'area sembrava la stessa, più o meno.
Comunque riprendendo questo commento precedente, in cui cito la possibilità di utilizzare Erone....
______________________________________________________________________
"Basterebbe applicare il teorema di Erone (che fornisce l'area del triangolo, noti i suoi lati) , ai 5 triangoli di lati:
9 17 x
6 8 x
6 7 y
29 (15+5) y
5 13 12
_________________________________________________________________
e assegnando x= 9 e y = 13 l'area che risulta, a conti fatti, è circa 190.
Da qui in poi non ci è ben chiaro, almeno fino ad ora, il percorso da intraprendere.
P.S. metti gli speroni di peluche...
grazie Mau (e Oreste), avete sapientemente corretto la figura riportandola a quella originaria...
Resta una piccolo problema di scelta... che è proprio quello che fa scattare i nostri cinque supereroi...ma comincio a scrivere la prima parte...