Come temevo questo quiz era troppo contorto e probabilmente frutto di una mia perdita di logica (dovuta al coronovirus, risaputo "tifoso" di Archimede?). Cerchiamo, allora, di riportarlo su binari più seri e comprensibili.

Innanzitutto, quello che chiedevo di fare attraverso la prima parte era riuscire a sezionare il mostro nel modo più utile per la seconda parte. Per far questo avevo cercato di fare un disegno ultra perfetto, in modo da poter misurare direttamente le lunghezze di ogni segmento ausiliario. Nella foga dei commenti scambiati con Maurizio ne avevo già evidenziati due (uno di 6 e uno di 5 metri, relativi alla "testa" e alla "coda"). Ne mancavano ancora almeno due importanti. E, a quel punto, bisognava fare la scelta giusta. Io, nei commenti scambiati con Maurizio, avevo sbagliato la figura e quindi si è aggiunto caos al caos.

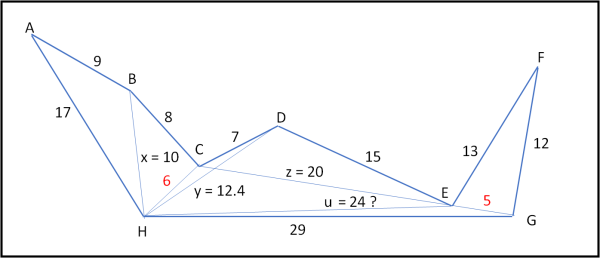
Torniamo, perciò, alla figura originaria dell'articolo ufficiale, che riporto di seguito con i valori di tutti i segmenti ancora da tracciare per ottenere delle sezioni del mostro triangolari. Una volta scelti i triangoli basta applicare la formula di Erone a ciascuno di loro e sommare le aree per avere quella finale del mostro. Ovviamente, qualsiasi sia la scelta fatta, l'area totale deve essere sempre la stessa.

Tuttavia, il suggerimento che avevo dato era chiaro: cercare segmenti la cui lunghezza fosse data da un numero intero. Vediamo allora la situazione...

Il segmento x (BH), checché ne dica Mau, viene uguale a 10 (ho provato e riprovato). Il segmento y (HD) ha, invece, un valore che viene uguale a 12.4. Il segmento z (CE) ha un valore esatto di 20. Il segmento u (HE) torna invece di 24.1, che potrebbe anche essere considerato un 24 intero.

Escludiamo quindi y tra i segmenti da scegliere. I triangoli possibili restano, allora, ABH, BHC, CDE, HCE, HEG e EFG. Sei triangoli... Ricordiamo, comunque, che Erone ci fornirebbe sempre lo stesso risultato per l'area totale, anche utilizzando y e altri possibili triangoli. L'area totale si trova essere:

A = 192

Tra parentesi, proprio come aveva detto in seconda battuta Maurizio, anche se aveva considerato la figura che io avevo inserita errata nei commenti... che pasticcione che sono...

Comunque sia, adesso la situazione dovrebbe essere abbastanza chiara e siamo pronti a rispondere alla seconda domanda:

In qualche modo si deve rendere inoffensivo il cetaceo o quello che è. Nessuno se la sente, però, di scendere in battaglia aperta. Si decide, perciò, di affidarsi ai soliti supereroi . In particolare ai cinque che sono rimasti sulla Terra (gli altri stanno compiendo imprese eccezionali oltre i Bastioni di Orione): Il loro capo indiscusso è Superhero, forse il più dotato di tutti, il vero rappresentante del gruppo dei salvatori della Terra. Però, però... malgrado si cerchino dappertutto, non rispondono ai richiami. Dove sono finiti, accidenti! Aiutatemi a ritrovarli, gli oceani sono -forse- in grave pericolo.

Posso aggiungere che finora abbiamo cercato di utilizzare normali eroi per sezionare nel modo migliore il mostro, ma adesso ci servono dei supereroi!

Va bene, va bene... sto continuando a farneticare un poco, ma di questi tempi "licet insanire", come diceva Seneca...

QUI trovate i cinque supereroi