Le prodezze del Teorema di Tolomeo proseguono, aiutandoci a dimostrare facilmente una proprietà poco conosciuta collegata ai triangoli equilateri e a finire in bocca alla sezione aurea. Con questo articolo finiamo la nostra piccola-lunga storia sul Teorema di Tolomeo, ma non è detto che non ci si ritorni  su, prima o poi.

Iniziamo col prendere un bel triangolo equilatero ABC e la circonferenza a lui circoscritta (Fig. 21).

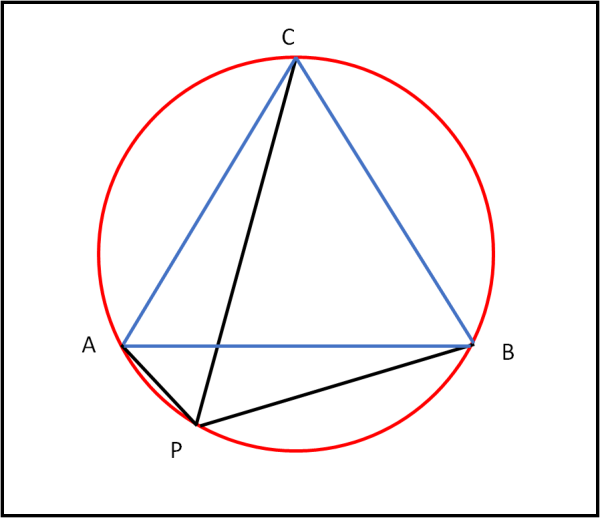
Nell'arco di circonferenza compresa tra A e B (ma andavano bene anche  B e C o C e A) scegliamo un punto P qualsiasi. Vale la relazione poco conosciuta:

AP + PB = PC

La dimostrazione non è facilissima, ma lo diventa se utilizziamo il Teorema di Tolomeo al quadrilatero APBC.

La somma del prodotto dei lati opposti deve essere uguale al prodotto delle diagonali.

Possiamo scrivere, allora:

AP CB + PB AC = PC AB

ma AB = CB = AC     (lati del triangolo equilatero)

Ne segue:

AP + PB = PC

ridicolo, veramente ridicolo...

Manteniamo sempre la nostra circonferenza, ma, questa volta, inscriviamo  al suo interno un pentagono regolare ABCDE (Fig. 22).

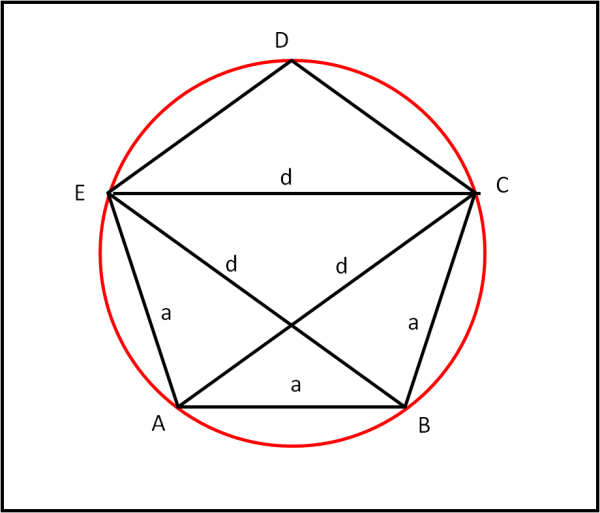
Conosciamo molte proprietà del pentagono, ma quella che più ci serve è che tutte le sue diagonali sono uguali  a d (così come pure i suoi lati sono tutti uguali ad a). Escludiamo pure dal nostro "gioco" il vertice D e analizziamo il trapezio isoscele ABCE. Ciò che vogliamo trovare è il rapporto tra d e a.

Basta chiamare in nostro soccorso Tolomeo...

Per il suo solito Teorema possiamo scrivere:

ad + aa = dd

d² - ad - a² = 0

dividendo tutto per a², si ha:

(d/a)²  - d/a - 1 = 0

Ma d/a è proprio il rapporto che volevamo trovare e possiamo chiamarlo x

x² - x - 1 = 0

Risolvendo la semplicissima equazione di secondo grado, otteniamo:

x = (1 +/-√(1 + 4))/2 = (1 +/-√5)/2

Escludiamo senz'altro la soluzione con il segno meno davanti alla radice di 5, dato che risulterebbe negativa (non ha senso un rapporto di segmenti negativo!) e consideriamo l'unica soluzione possibile:

d/a = (1 +√5)/2

Ma quanto trovato non è altro che la celeberrima sezione aurea, tanto usata nell'architettura dell'antica Grecia e non solo.

Lo stesso rapporto a cui tende la non meno celebre serie di Fibonacci. Per saperne di più su questo rapporto e su Fibonacci potete leggere QUI.

 

QUI tutti gli articoli dedicati al Teorema di Tolomeo