Soluzione al Quiz: Un grafo con sei vertici **
Il quiz lo trovate qui.
Sostanzialmente, mi sembra che Maurizio abbia imbroccato la soluzione, anche se con la sua metodologia empirico-intuitiva che secondo me lo contraddistingue. Vi dò una soluzione un po' più formale al quiz, semplice e concisa. Ho aggiunto due figure per capirci meglio , Scusate per la loro rozzezza.
La domanda era questa:
Chiamiamo un grafo completo con 6 vertici, ovvero un grafo in cui ogni vertice è collegato con tutti gli altri. E' vero o falso che, comunque colorando i lati del grafo con due colori, esiste sempre un triangolo monocromatico contenuto in esso?
InK5, avevamo visto che non è possibile. In K6 si, qualsiasi sia la colorazione.
Infatti, supponiamo di aver colorato con due colori b rosso e nero e c il lati di K6, e sia v0 un vertice fissato; poichè v0 ha grado 5, per il principio dei cassetti (i lati sono 5 , e le colorazioni sono 2), almeno tre lati che partono da esso hanno lo stesso colore; siano {v0,v1}, {v0,v2} e {v0,v3} tali lati, e sia rosso il loro colore.
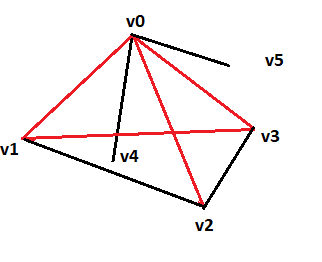
Se uno tra i lati {vi,vj}, 1 ≤ i < j ≤ 3 *, ha colore rosso allora il triangolo indotto da {v0,vi,vj} è monocromatico; se invece tali lati hanno tutti colore nero allora è il triangolo indotto da {v1,v2,v3} ad essere monocromatico. Dunque, ogni colorazione con due colori di un grafo completo con almeno sei vertici contiene un triangolo monocromatico.
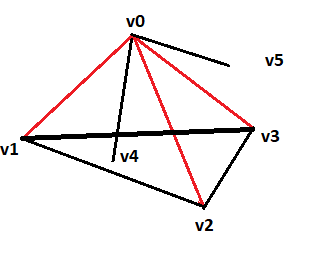
Bene, vedremo fra breve a cosa servirà questo risultato.
- La scrittura {vi,vj}, 1 ≤ i < j ≤ 3 non è niente di trascendentale; è un modo condensato per descrivere l'insieme dei lati {v1,v2}, {v1,v3},{v2,v3}.





