Un altro modello matematico, detto anche SIS *** (Di Umberto e Maurizio)

Categorie: Matematica Tags: modelli matematici Scritto da: Umberto Cibien Commenti:1

Questo articolo costituisce il seguito all'articolo REALTÀ E RAPPRESENTAZIONE : I MODELLI MATEMATICI. Ripeto, come nella premessa, non è necessaria alcuna conoscenza delle equazioni differenziali, ma solo del concetto di derivata , e dell'integrale di 1/x , assieme alla derivata del logaritmo. Il termine equazione differenziale può spaventare; ma non è altro che una equazione dove compare una funzione incognita assieme alla sua derivata. Quindi niente di trascendentale. D'altronde , ormai la scuola superiore fornisce questi concetti sia agli istituti commerciali che a quelli professionali ; basta un po' di buona volontà per la comprensione dei calcoli che purtroppo sono alla base dei modelli. Dopo aver trattato il modello SI, tratteremo ora il modello SIS. Ma vediamo cos'è...

Nella realtà che ci circonda possiamo osservare che, in tema di conoscenza, lo stato di ciascun individuo è mutevole.

Ci sono persone che acquisiscono conoscenze e le utilizzano, conservandole, mentre altri, dopo averle acquisite le lasciano cadere nel dimenticatoio.

E’ il fenomeno del cosiddetto analfabetismo-di-ritorno, citato nel precedente articolo.

Oltre a questa “cancellazione della memoria”, che nel nostro Pese si manifesta in quasi un terzo della popolazione, e attiene a conoscenze di base, esiste una diversa causa determinante per la perdita di valore della conoscenza , un fattore che agisce su tutta la popolazione, su gruppi professionali omogenei , ed è la obsolescenza delle tecnologie.

Mentre i contenuti di base, consolidati e immutabili sono stabili, le nozioni legate al tumultuoso mondo delle tecnologie sono in continuo ribollire, evaporano e sublimano in tempi brevissimi.

Il termine abusato di “nuove tecnologie” andrebbe riformulato come “tecnologie correnti”, perché “nuove” potranno esserlo solo per un tempo limitato, come le notizie di un quotidiano. Chi oggi le possiede, chi ha la conoscenza dei loro meccanismi segreti, si ritroverà a dover ricominciare a studiare da capo, quando l’onda impetuosa del cambiamento le sostituirà con altre.

Questo fatto è il vero motore degli investimenti per la riqualificazione professionale, la continuing education, il modello di formazione permanente che consente ai singoli individui e alle organizzazioni di aggiornare e sviluppare le conoscenze e le tecniche.

Useremo ancora, in questo nuovo modello, la lettera S e la lettera I con i nuovi significati:

I = istruiti e S = superati, nel senso che posseggono conoscenze “superate” non più utilizzabili

Nella popolazione di N individui che si trovano in parte nello stato S e in parte nello stato I, si presenterà quindi una dinamica di migrazione tra i due stati. All’apparire delle innovazioni, una parte degli I tornerà allo stato S e solo attraverso il processo di riqualificazione potrà di nuovo raggiungere la condizione di Istruito.

Il modello descritto nel precedente articolo che non contemplava questa ipotesi, il modello S I , dovrà essere esteso per rappresentare la mutevolezza dello stato, dovuta alla evoluzione della tecnologia.

Diverrà quindi un modello S I S. (Superati ---> Istruiti---> Superati) che dinamicamente raffigura la ciclica oscillazione dello stato individuale.

La popolazione degli Istruiti, in un certo momento sarà composta da persone che, per la loro professione, non sono impattate dal cambiamento e persone innovatrici che detengono la nuova conoscenza Sono proprio costoro che la trasferiranno agli individui del loro gruppo professionale divenuti S, da riqualificare. Nella nostra ipotesi ciascuno dei riqualificati può a sua volta istruire altri, anche se in pratica, sfortunatamente, questo avviene solo in modo limitato.

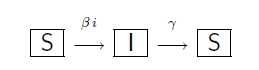
Al solito indichiamo con i,s i rapporti percentuali rispetto alla popolazione totale N, che del resto è una costante. Quindi i=I/N,s=S/N, i+s=N/N=1
Supponiamo che la durata media della istruzione sia $\frac{1}{\gamma }$ , si ottiene il sistema di
equazioni differenziali:

(equazioni, ripeto, che hanno come incognita una funzione che compare anche con la sua derivata).

Ma da dove le facciamo saltar fuori?

nell’unità di tempo una frazione costante $\beta$ del numero degli incontri possibili risulta efficace per la trasmissione dell'istruzione;
nell’unità di tempo una frazione costante γ del numero degli istruiti torna ad essere nella classe dei superati.
D'ora in poi chiameremo semplicemente con l'iniziale S i superati e con l'iniziale I gli istruiti

$\Delta S=-\beta S\frac{1}{N}\Delta t +\gamma i\Delta t$

infatti, nell'intervallo di tempo $\Delta t$ , i soggetti S diminuiranno della quantità $-\beta S\frac{1}{N}\Delta t$ mentre invece diminuiranno della quantità $-\gamma i\Delta t$ ;

$\Delta I= \beta \frac{1}{N }S\Delta t- \gamma i \Delta t$

analogamente , i soggetti I nell'intervallo di tempo $\Delta t$ aumenteranno di $\beta S\frac{1}{N}\Delta t$ e poi

dividiamo per $\Delta t$ e al posto di $\frac{1}{N}S$ scriviamo s come da definizione,s=S/N.

$\Delta S/\Delta t=-\beta si+\gamma i$

$\Delta I/\Delta t= \beta si- \gamma i$

Il termine - $\beta si$ indica il tasso di movimento dalla classe dei superati a quella degli istruiti;

il termine - $\gamma i$ dà il tasso a cui gli istruiti ritornano nella classe dei superati.

il passaggio al limite, per $\Delta t\rightarrow 0$ , propone le equazioni differenziali:

Sappiamo che s + i = 1 per ogni tempo t.

Poniamo:

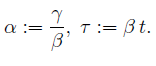
Quindi la funzione s risolve l'equazione:

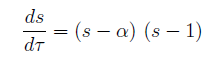
infatti

$\frac{ds}{dt}=-\beta si + \gamma i$ ;

$\frac{ds}{\beta dt}=-\beta si + \gamma i=\frac{-\beta si + \gamma i}{\beta }$

$\frac{ds}{d\tau }=-si+\gamma i/\beta$ ;

ma $\gamma /\beta =\alpha$ , i=1-s, sostituendo si ottiene

$\frac{ds}{d\tau }=-si+\gamma i/\beta=-s(1-s)+\alpha (1-s)$

in definitiva:

$\frac{ds}{d\tau }=(s-1)(s-\alpha )$

invertiamo adesso la frazione a sinistra ( in realtà questo andrebbe giustificato con i metodi rigorosi dell'analisi, chissà, forse un giorno potremmo provare); dopo questo passaggio, almeno per il momento, dobbiamo supporre $\alpha \neq 1$

Applicando il metodo di separazione delle variabili otteniamo:

(la variabile s e la sua derivata devono comparire dalla stessa parte dell'equazione)

$\frac{d\tau}{ds }=\frac{1}{(s-1)(s-\alpha )}$

ma, $\frac{1}{s-1}-\frac{1}{s-\alpha }=\frac{s-\alpha -s+1}{(s-1)(s-\alpha )}=\frac{1-\alpha }{(s-1)(s-\alpha )}$

quindi

$\frac{d\tau}{ds }=\frac{1}{(s-1)(s-\alpha )}=\frac{1}{s-1}-\frac{1}{s-\alpha }=\frac{s-\alpha -s+1}{(s-1)(s-\alpha )}=\frac{1-\alpha }{(s-1)(s-\alpha )}$

ma allora:

$(1-\alpha )\frac{d\tau}{ds }=\frac{1}{(s-1)(s-\alpha )}$

$d\tau=\frac{1}{1-\alpha }\frac{1}{(s-1)(s-\alpha )}ds$

Concentriamoci sul calcolo di $s(\tau)$ , e facciamolo in modo differente dall'altro articolo, ovvero in modo più compatto.

Integriamo l'eguaglianza fra le due quantità infinitesime, da 0 a $\tau$

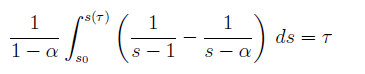
banalmente, infatti, $\int_{0}^{\tau}d\tau=\tau$ ;

Calcoliamo l'altro integrale (notare che se C varia da 0 a $\tau$ , s varia da s(0) a $s(\tau)$ .

calcoliamo prima l'integrale indefinito, spezzandolo in due parti; sono semplici primitive che si ottengono dai logaritmi:

$\int \frac{1}{s-1}=ln (s-1)$ ; $-\int \frac{1}{s-\alpha }=-ln(s-\alpha )$

$\tau=[\frac{1}{1-\alpha }(ln(s-1)-ln(s-\alpha )]_{s_{0}}^{s}$

$\tau=\frac{1}{1-\alpha }[(ln(s-1)-ln(s-\alpha )-(ln(s_{0}-1)-ln(s_{0}-\alpha ))]$

$\tau=\frac{1}{1-\alpha }[ln(s-1)-ln(s-\alpha )-ln(s_{0}-1)+ln(s_{0}-\alpha )]$

e, passando agli esponenziali:

$e^{(1-\alpha )\tau}=\frac{(s-1)(s_{0}-\alpha )}{(s-\alpha )(s_{0}-1)}$

e alla fine , isolando s:

(ometto ulteriori passaggi algebrici, perchè sono molto noiosi; si tratta di isolare la variabile s, e magari porre per comodità $k=e^{(1-\alpha )\tau}$ per fare i conti)

Nel caso $\alpha =1$ l'integrale è un po' più semplice

$\alpha =1, \frac{d\tau}{ds }=\frac{1}{(s-1)(s-\alpha )}=\frac{1}{(s-1)^{2}}$

$\tau=\int_{s_{0}}^{s(\tau)} \frac{1}{(s-1)^{2}}ds$

(spero che tutti sappiano che la primitiva di $\frac{1}{(s-1)^{2}}$ è $- \frac{1}{(s-1)}$ )

e otteniamo invece:
.
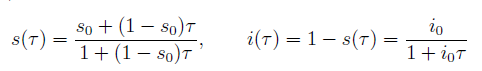Ma veniamo adesso al comportamento asintotico dell'equazione differenziale i(t), conoscendo i valori iniziali ,
$s_{0}=s(0), i_{0}=i(0)$
Poniamo :
$\sigma=\beta /\gamma$ , quindi $\alpha =\frac{1}{\sigma}$
$\sigma$ viene detto soglia critica per tale sistema, ed è il prodotto tra il tasso di contatto $\beta$ e il tempo medio di ritorno alla classe dei superati, $1/\gamma$ , Ed eccoci arrivati al comportamento asintotico;dobbiamo studiare il limite della funzione i(t) per $t\rightarrow +\infty$

la funzione, espressa in funzione di $\tau$ è la seguente:

il limite per $t\rightarrow +\infty$ è equivalente a cercare il limite di questa funzione (essendo $\tau=\beta t$ ) per $\tau\rightarrow +\infty$

Se l'esponente di e è negativo, ossia se $1-\alpha <0$ , il limite è 0; ma $\alpha =1/\sigma$ , $1<1/\sigma$ , $\sigma<1$ , E anche se $\sigma=1$ , essendo $(1-\alpha )=0$ .

Se l'esponente di e invece è positivo, nel qual caso $\isgma>1$ , dividendo numeratore e denominatore della funzione i per $e^{(1-\alpha )\tau}$ , per $\tau\rightarrow \infty$ , otteniamo:

$\frac{(1-\alpha)i_{0} }{\frac{1-\alpha }{\infty}-\frac{1}{\infty}+i_{0}}\rightarrow 1-\alpha =1-1/\sigma$

In definitiva:

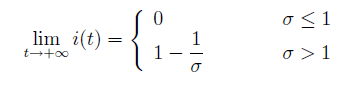
Essendo $\sigma=\beta /\gamma$ , se $\gamma >\beta$ gli istruiti tendono a zero ( questo è intuitivo; se il tasso di ritorno alla classe dei superati è maggiore del tasso al passaggio di istruiti, gli istruiti sono destinati a scomparire. Se $\beta >\gamma$ , avremo una percentuale di istruiti che restano, tanto più grande quanto maggiore è $\sigma$ . Mutatis mutandis..

Ma vediamo adesso la cosa dal punto di vista grafico. Sostituiamo a $\tau\rightarrow \beta t$ , per avere a che fare adesso con t.

Si tratta di studiare la funzione:

$i(t)=\frac{(1-\alpha )i_{0}e^{(1-\alpha )\beta t}}{1-\alpha +i_{0}(e^{(1-\alpha )\beta t})-1)}$

$i(0)=i_{0}$ ; ; quindi i conti tornano (infatti se poniamo t=0 otteniamo $\frac{(1-\alpha )i_{0}e^{0}}{1-\alpha +i_{0}(1-1))}=i_{0}$ )

nei due casi, $\sigma \leq 1$ e $\sigma >1$ ;

Affidiamoci però a software tipo desmos, per evitare di prolungare troppo il discorso (basterebbe eseguire la derivata prima di i(t) e studiarne il segno, i limiti asintotici li conosciamo già).

Nel prossimo articolo ci aspetterà il modello SIR. Vedremo cos'è

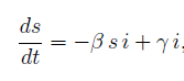
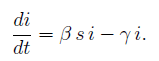
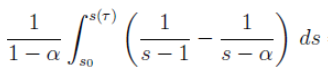
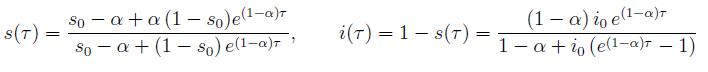
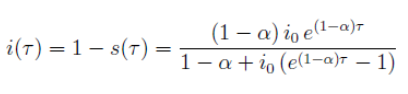
1 commento

leandro

30/03/2020 at 15:26

Per quanto mi ricordo vagamente il modello preda predatore di Lotka-Volterra prevede soluzioni non stabili (orbite). Ma nel modello manca il vincolo i+s = 1. Forse è questo vincolo che stabilizza la soluzione.

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

L	M	M	G	V	S	D
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

Un altro modello matematico, detto anche SIS *** (Di Umberto e Maurizio)

Articoli correlati

Soluzione del "banale" esponente **

(Q) Un semplice esponente ... **

Soluzioni dello scontro evitato **/***

Evitiamo uno scontro **/***

1 commento

Lascia un commento Cancel Reply

Soluzioni dello scontro evitato /*

Evitiamo uno scontro /*