QUI il quiz      QUI la prima parte della soluzione

 

Chi è il quarto amico?

Ridiamo la parola a un nuovo personaggio che sembrerebbe essere quello mancante...

Buon giorno, il mio nome è incentro e non è difficile trovarmi: basta costruire le bisettrici dei tre angoli del triangolo. Nel far questo vi accorgereste che io divento anche il centro del cerchio inscritto nel triangolo (è cosa facilissima dimostrarlo).

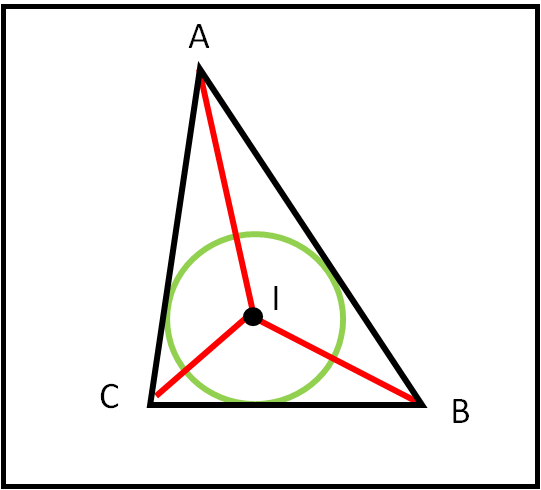
Purtroppo (almeno per voi) non sono io (I) il quarto amico. In realtà una volta lo ero, ma poi mi sono accasato e riesco a trovarmi con loro solo in casi eccezionali. Ad esempio, quando il triangolo è isoscele riesco a mettermi in linea con loro e, addirittura, quando il triangolo è equilatero COINCIDIAMO perfettamente tutti e quattro. Ma per triangoli qualsiasi, quelli più comuni, io non posso più partecipare alle vecchie riunioni al bar o lungo la strada.

Vi devo svelare un piccolo grande segreto … in realtà, i miei tre amici, che non riesco più a incontrare come una volta, hanno moltissimi altri potenziali amici che li seguono perfettamente in linea, una vera moltitudine (guardate QUI per conoscerli tutti). Tuttavia, ortocentro, baricentro e circocentro se la tirano un po’, data la semplicità con la quale riescono a mettersi in mostra. Gli altri, che vorrebbero entrare nel loro ristretto gruppo di amici “particolari”, devono utilizzare costruzioni molto complicate e -a volte- quasi assurde. Insomma, che li seguano pure, ma per i nostri tre amici non esistono proprio.

Tra loro, però, ce n’è uno che alla fine li ha convinti, malgrado sia un po’ più difficile da costruire. Soprattutto li ha convinti la sua posizione veramente centrale sotto certi punti di vista e la sua eleganza. Ma, adesso, devo ritirarmi (mia moglie mi aspetta … se no sono guai!) e lascio la parola proprio a lui.

Il quarto amico

Buon giorno, mi presento con il mio nome più comune: centro del cerchio dei nove punti.  Ma, se volete fare più scena, potete chiamarmi centro del cerchio di Feuerbach o, se preferite rimanere in tema con la soluzione finale del lungo problema di amicizia che abbiamo affrontato, centro del cerchio di Eulero (anche se a scoprirmi non è stato lui, ah… la celebrità!).

Vi dico subito che la trattazione sarà un po’ lunga e abbastanza articolata. La lunghezza dipende essenzialmente dal volere spiegare i vari passaggi in modo elementare e comprensibile a tutti, anche a coloro che conoscono poco più dei triangoli simili e del teorema di Talete sulle rette parallele. Una trattazione noiosa? Può anche darsi, ma vi assicuro che diventa una specie di giallo a mano a mano che si svelano tutti i “trucchetti” da utilizzare. Insomma, oltre alla difficoltà di descrivermi, risulta alquanto innovativa (per qualcuno di voi, almeno) la ragione per cui sono diventato amico così stretto dei tre punti, ben più famosi e facili da identificare.

Andiamo per gradi, iniziando a dire chi sono realmente e come vengo costruito.

Scegliamo i nove punti

Come dice il mio stesso nome, occorrono ben nove punti per trovarmi, nove punti che sono in qualche modo connessi agli amici precedenti, in particolare con l’ortocentro.

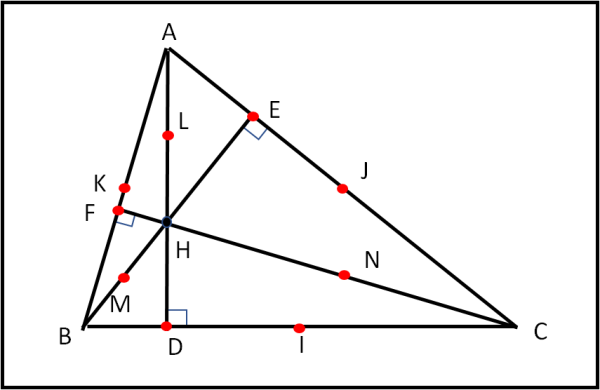
Partiamo, allora, dal solito triangolo ABC (in Fig. 8 lo abbiamo leggermente cambiato per vedere meglio certe costruzioni) di cui conosciamo già l’ortocentro H e proprio da quest’ultimo costruiamolo nuovamente, segnando per bene (in rosso), i tre punti in cui le altezze vanno a toccare i lati (D,E,F).

Indichiamo poi, altrettanto chiaramente, i punti di mezzo di ogni lato (I, J, K). E siamo  arrivati a 6. Consideriamo adesso i segmenti che uniscono l’ortocentro H con i tre vertici del triangolo e dividiamoli a metà, segnando questi punti di mezzo come L,M e N. E siamo arrivati a 9. Bene, forse l’avete già intuito, ma per questi nove punti passa un bellissimo cerchio, al cui centro sto proprio io, l’ultimo amico!

Il primo problema è, però, dimostrare che per questi nove punti passa veramente un cerchio. Proviamoci con molta calma e attenzione. Poi ci dedicheremo anche a me, il suo centro …

Il cerchio dei nove punti è proprio un… cerchio

Innanzitutto, abbiamo bisogno di evidenziare delle rette parallele tra di loro (Fig. 9).

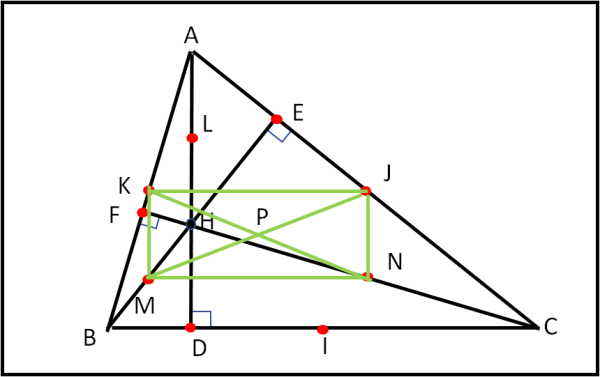
Consideriamo l’altezza AD e il triangolo ABH. Il segmento KM passa per i punti medi dei lati AB e BH (per costruzione). Ciò vuol dire, grazie a Talete, che  i due segmenti KM e AH sono paralleli tra loro. Se sono paralleli tra loro anche KM deve essere perpendicolare a BC. Non solo però, possiamo anche dire che:

2KM = AH

dato che la proporzionalità tra i lati dei due triangoli è di 2 a 1 per costruzione di K e di M.

Passiamo, adesso, ai triangoli AHC e JNC. Per le stesse motivazioni dei triangoli precedenti, possiamo dire che JN è parallelo ad AD e che

2JN = AH

Da queste due relazioni possiamo concludere che:

KM = JN

E che

KM // JN     (paralleli tra loro)

In quanto entrambi perpendicolari a BC o, se preferite, entrambi paralleli ad AH.

Passiamo, ora, a considerare i triangoli HBC e HMN. Vale sempre lo stesso gioco dei triangoli precedenti, per cui:

MN // BC

2MN = BC

Consideriamo, infine, il triangolo ABC e il triangolo AKJ. Anche per loro valgono le relazioni:

KJ //BC

2KJ = BC

Ne segue che:

KJ = MN

e

KJ // MN

Guardiamo con attenzione il quadrilatero KMNJ. Esso, per quanto appena trovato, ha i lati opposti uguali. Non solo, però … ricordiamo che sia KM che JM sono perpendicolari a BC. Ma se sono perpendicolari a BC devono esserlo anche a KJ e a MN che sono paralleli a BC. Ne segue che il quadrilatero ha anche gli angoli interni retti, ossia è un rettangolo.

Se è un rettangolo, però, deve poter essere inscritto in un cerchio e l’intersezione delle sue diagonali (diametri) devono individuare il centro P (detto fra noi, sono proprio io, il centro del cerchio dei nove punti). Tuttavia, non possiamo fare le cose troppo facili … anche se si vede chiaramente che questo cerchio passa anche per i restanti 5 punti … Dobbiamo dimostrarlo! Cominciamo intanto a segnare in rosso, in Fig. 10, i quattro punti che appartengono sicuramente al cerchio di centro P.

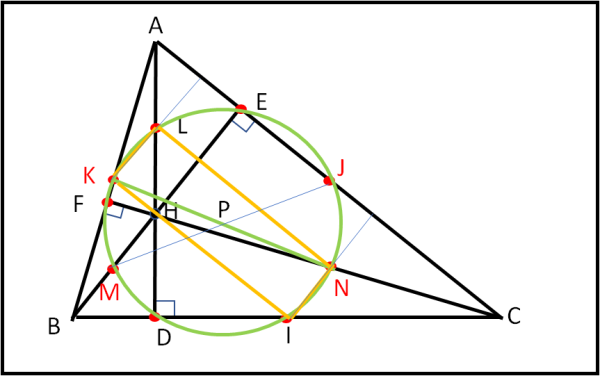
Procedendo in modo analogo alla prima parte, possiamo dire che KL è parallelo a BE e quindi perpendicolare ad AC. Dalla similitudine dei triangoli ABH e AKL, abbiamo inoltre che BH = 2 KL.  Adottando lo stesso “trucchetto” ai triangoli BHC e INC, otteniamo che BH = 2IN e si ha inoltre che IN è parallelo a KL. Da quanto appena detto risulta KL = IN. Basta poi passare ai triangoli AHC e HLN per concludere che AC = 2LN, mentre i triangoli ABC e KBI ci dicono che AC = 2KI. Per cui anche LN = KI oltre che paralleli a BE. Quasi ormai annoiati, è facile concludere che KL  e IN sono perpendicolari ad AC e quindi anche a LN e KI, da cui anche il quadrilatero KLNI è un rettangolo.

Attenzione, però: questo rettangolo ha la stessa diagonale KN del rettangolo precedente e quindi il cerchio circoscritto a lui è lo stesso cerchio di prima e ha sempre come centro il sottoscritto P.

Altri due punti (L e I) dei famosi nove punti di partenza appartengono, perciò, allo stesso cerchio di centro P e diametro KN. Possiamo colorare in rosso anche loro, in Fig. 11 …

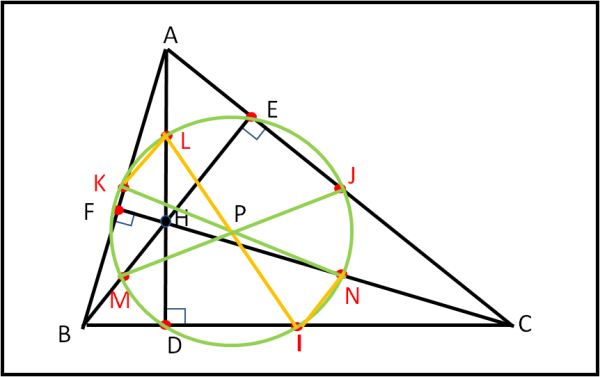
Ci mancano solo tre punti … F, E e D. Ma ormai siamo in dirittura d’arrivo. Basta accorgersi che LI, MJ e KN sono tre diametri del cerchio e ricordare che gli angoli FKN, MEJ e LDI sono retti. Accidenti … ma, se un triangolo rettangolo ha come ipotenusa un diametro, il suo vertice, corrispondente all’angolo retto, deve stare sul cerchio: di conseguenza, questo è anche il destino di F, D ed E.

Sei più tre uguale a nove … Ci siamo riusciti! Disegniamolo in Fig. 12 e io, P, sto comodamente al suo centro

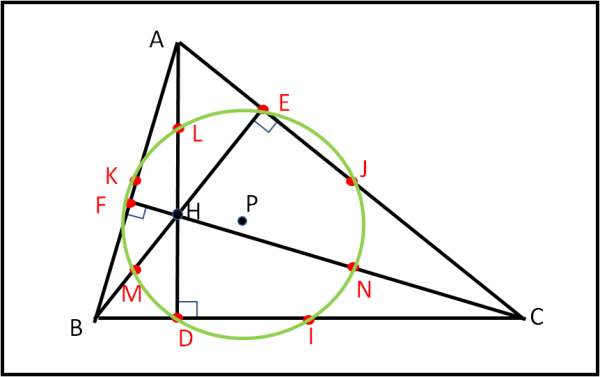
Purtroppo, però, non è ancora finita. Ci manca l’ultima parte, quella che dimostra che anch’io faccio parte della retta di Eulero e che occupo una posizione veramente centrale. Ovviamente, non ho bisogno di dimostrare che sono il linea con tutti e tre i punti … me ne bastano due, dato che il terzo abbiamo già dimostrato che segue il movimento degli altri due.

Occupiamoci, perciò, di studiare la mia posizione rispetto all’ortocentro e al circoncentro del triangolo ABC di partenza.

Ci sono vari modi per  riuscirci, ma permettetemi di usare un metodo molto elegante che ci permetterà di affrontare un nuovo tipo di trasformazione nel piano, decisamente più semplice della geometria inversiva, ma non per questo meno interessante.

L' Omotetia

Definita con parole semplici, essa è una particolare trasformazione geometrica del piano (ma anche dello spazio) che dilata o contrae una qualsiasi figura, mantenendo invariati gli angoli, ossia la forma.

Diamone anche la definizione più “formale” che ci permetterà di arrivare, a piccoli passi, al caso che ci interessa da vicino.

Consideriamo un punto A (centro dell’omotetia) e un punto P qualsiasi del piano. Scegliamo inoltre un fattore k non nullo. La trasformazione fa corrispondere a ogni punto P un punto P’, tale che AP’/AP = k. Vediamo questo caso generale nella Fig.  13.

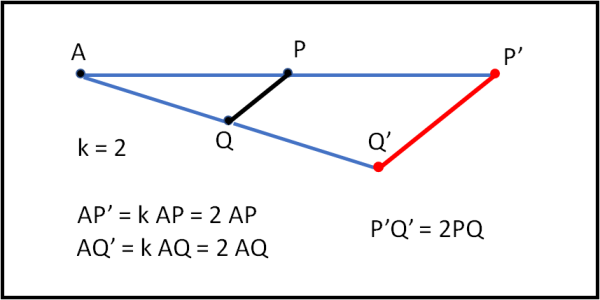
Nella figura abbiamo considerato due punti (P e Q) e li abbiamo trasformati in P’ e Q’, utilizzando il rapporto k = 2. Uniamo P con Q e P’ con Q’. Notiamo subito che ci troviamo di fronte a due triangoli simili APQ e A’P’Q’, dove per la solita ragione ormai stranota PQ è parallelo a P’Q’. Ma è anche vero che P’Q’ = 2 PQ. In pratica, la trasformazione ha preso il segmento PQ e lo ha trasformato in  un segmento P’Q’ di lunghezza doppia rispetto a PQ.

Niente ci vieta, allora, di considerare una figura nel piano, ad esempio il triangolo QPR, e trasformarlo nel triangolo Q’P’R’, utilizzando sempre il rapporto k = 2 (Fig. 14).

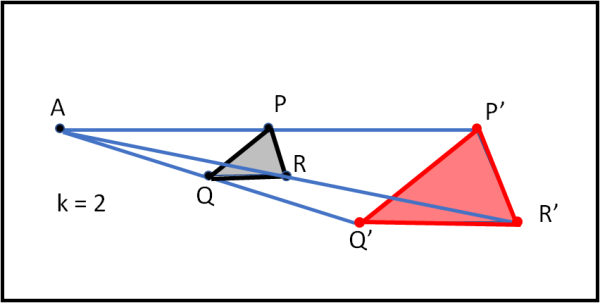
Beh… ho quasi vergogna a dimostrare che PQR e il suo trasformato P’Q’R’ sono triangoli simili. Basta considerare le coppie di triangoli APR e AP’R’, ARQ e AR’Q’, APQ e AP’Q’. PQR e P’Q’R’ sono simili e il rapporto di proporzionalità dei loro lati è ancora k = 2.

Tanto che ci siamo, parliamo anche di omotetia inversa, ossia quella in cui k è scelto negativo. La Fig. 15 ci mostra il triangolo PQR ribaltato dall’altra parte di A

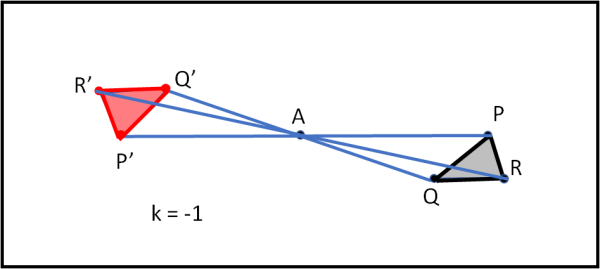
In questo caso il “trasformato” è il triangolo P’Q’R’ che, essendo k = -1, ha le stesse dimensioni di quello originario, ma si trova ribaltato rispetto ad A. Restano immutate le condizioni di similitudine (anzi, in questo caso, addirittura di uguaglianza o congruenza come si dice adesso).

Ovviamente, non c’è problema a utilizzare un rapporto k minore di 1. In tal caso sarebbe il triangolo grande a trasformarsi nel triangolo piccolo e la figura resterebbe la stessa (Fig. 16 simile alla Fig. 14).

 

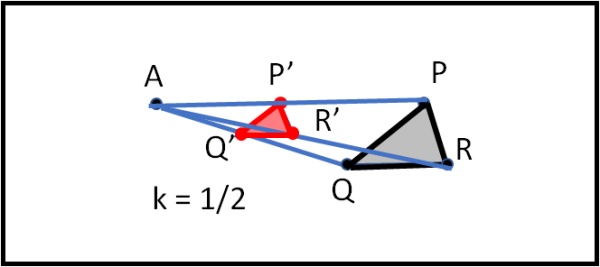
In generale, va compreso bene che non vi è solo una trasformazione dei vertici e dei lati, ma di tutti i punti interni al triangolo, compresi, perciò, sia il baricentro che l’ortocentro e il circocentro. Non dimentichiamolo …

Ancora più interessante per il nostro scopo è il caso in cui il centro dell’omotetia sia interno alla figura geometrica che vogliamo trasformare. Facciamone subito un esempio in Fig. 17, considerando il solito triangolo.

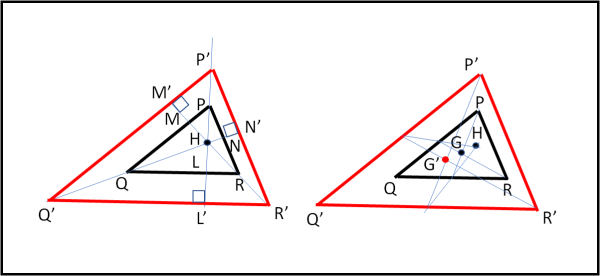
A sinistra mostriamo la trasformazione eseguita prendendo come centro proprio l’ortocentro H: ben poco cambia rispetto a prima, il triangolo si dilata o si restringe (a seconda di quello che abbiamo preso come figura di partenza). Notiamo, a destra, come il punto H rimanga uguale a se stesso, mentre G, ad esempio, si sposti in G’, ma in modo tale che HGG’ restino collineari (ovviamente, dato che HG è la retta di trasformazione di G) e come GG’ mantenga le proporzioni di tutti gli altri punti del triangolo.

A questo punto non ci resta che considerare come figura da trasformare un bel cerchio. Il centro dell’omotetia lo prendiamo interno (Fig. 18)

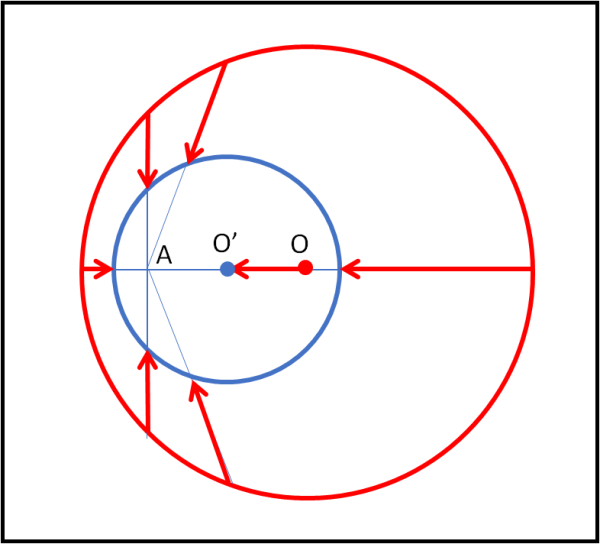
Il centro di proiezione è A e il  cerchio da trasformare è quello grande. Come k abbiamo scelto 0.5, ossia ½. Ogni punto del cerchio grande viene spostato sul cerchio azzurro, in modo che le distanze da A siano tutte dimezzate. Particolarmente importante è il fatto che il centro O del cerchio grande si sposta nel punto O’ del cerchio piccolo, rimanendone il centro.

Il quarto amico si allinea

Beh … penso che tutti ormai abbiano capito come applicare l’omotetia al nostro caso particolare. Disegniamolo in Fig. 19, lasciando solo le parti essenziali. Inseriamo, però, anche il cerchio circoscritto al triangolo ABC  e il suo centro C, che altri non è che il circocentro del triangolo ABC. Come centro di omotetia prendiamo proprio l’ortocentro H del triangolo ABC. Infine, come rapporto k utilizziamo nuovamente ½.

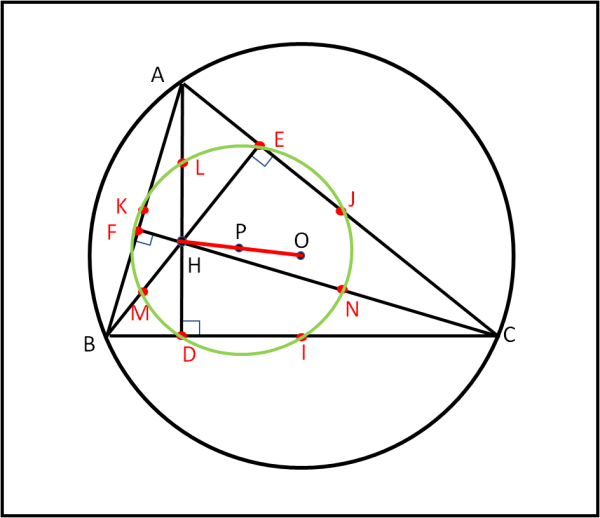
Beh… H resta se stesso, ma A si trasferisce in L, così come B in M e C in N. In poche parole il cerchio grande che contiene A, B e C si trasforma nel cerchio piccolo che contiene L, M e N. Ma questo cerchio non è altro che il cerchio dei nove punti. Il che vuol dire che il centro O (circocentro del triangolo ABC) si deve trasferire in P, mantenendo il rapporto dell’omotetia, ossia ½. In altre parole:

HP = ½ HO.

Ne consegue che il centro del cerchio dei nove punti non solo sta sulla retta di Eulero (HO) ma occupa proprio la posizione centrale tra H e O (HP = PO).

Notiamo bene che potevamo fare il procedimento all’inverso, partendo dal cerchio dei nove punti e trasformarlo nel cerchio circoscritto, usando il rapporto k = 2. Nulla cambiava.

A questo punto non abbiamo nessun problema a segnare anche il baricentro G (senza nemmeno bisogno di ricavarlo graficamente), ricordandoci che sta tra ortocentro e circocentro a una distanza doppia rispetto all’ortocentro di quanto non stia rispetto al circocentro.

In Fig. 20 vediamo i nostri quattro amici, nella loro posizione normale. Le distanze hanno come unità la distanza tra  centro del cerchio dei nove punti e baricentro.

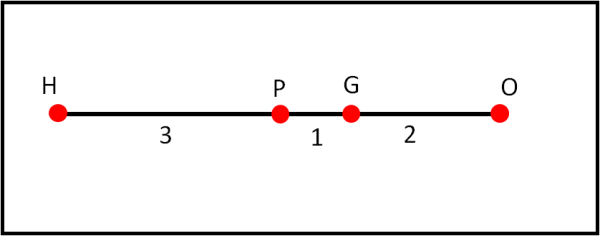
Come volevasi dimostrare, se anche due soli di noi si allontanano o si avvicinano, gli altri due devono immediatamente modificare la loro posizione. Siamo o non siamo quattro veri amici? Quasi come i 4 moschettieri!