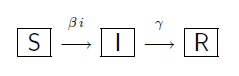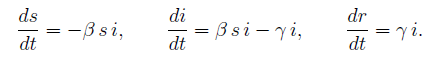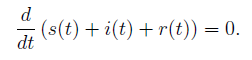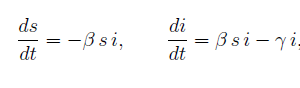Ancora un modello matematico:Il SIR *** (di Maurizio e Umberto)

Categorie: Matematica Tags: modelli matematici Scritto da: Umberto Cibien Commenti:0

Nel processo di riqualificazione che abbiamo descritto nel precedente articolo, sul modello SIS, si ipotizzava che la popolazione totale restasse costante. La somma delle due percentuali, Istruiti e Superati, valeva quindi costantemente 1.

Introduciamo una nuova ipotesi che tenga conto di un fenomeno di “abbandono”.

Vale a dire che, tra tutti coloro che periodicamente rientreranno nel circolo della formazione continua, vi saranno alcuni che abbandoneranno. Li individueremo con il termine R per Ritirati.

I motivi dell’abbandono non sono ovviamente rilevanti: volontaria o imposta è comunque una uscita dal sistema. E' un destino comune esaurire la spinta a riciclarsi, e scegliere di mettersi da parte. Anche per quelli bravi arriva il momento.

E quelli veramente molto bravi sono i più critici verso sé stessi. come vediamo qui...

Il modello diventerà quindi di tipo S I R in cui, alla nota dinamica S I S ,si sovrappone la perdita di popolazione dovuta agli R.

s + i + r = 1 sarà la nuova ripartizione delle rispettive percentuali degli stati possibili.

Due note importanti per la lettura; parleremo di s e S per distinguere percentuali rispetto alla popolazione e valori assoluti. Nella prima parte formale, studieremo le funzioni i, s come funzioni parametriche del tempo; nella seconda troveremo dei valori importanti per lo studio reale risolvendo il sistema di equazioni che lega s a i; r se richiesto verrebbe calcolato dall'equazione r=1-s-i .

Riprendendo quanto fatto nell'ultimo articolo, le equazioni da inserire nel modello sono le seguenti:

Ricordiamoci prima il ruolo di $\beta ,\gamma$ ;

nell’unità di tempo una frazione costante $\beta$ del numero degli incontri possibili risulta efficace per la trasmissione dell'istruzione; quindi la variazione della popolazione dei Superati sarà descritta da questo bilancio:

$\Delta s=-\beta S\frac{1}{N} i \Delta t$ ; essendo $s=S/N$ se dividiamo poi per $\Delta t$ otteniamo:

$\frac{\Delta s}{\Delta t}=-\beta si$ ; e il passaggio al limite ci dà la prima equazione:

$\frac{ds}{dt}=lim_{\Delta t\rightarrow 0}\frac{\Delta s}{\Delta t}=-\beta si$

2. nell’unità di tempo $\Delta t$ una frazione costante γ del numero degli istruiti va a finire nella classe R dei Ritirati.

$\Delta r=\gamma i\Delta t$ da cui segue il rapporto incrementale:

$\frac{\Delta r}{\Delta t}=\gamma i$ il passaggio al limite, per $\Delta t\rightarrow 0$ , porta alla equazione differenziale:

$\frac{dr}{dt}=lim_{\Delta t\rightarrow 0}\frac{\Delta r}{\Delta t}=\gamma i$

3. Passiamo infine alla dinamica degli Istruiti. Per essi avremo un flusso in entrata e uno in uscita:

Il termine $\beta si$ indica il tasso di movimento dalla classe dei superati a quella degli istruiti (in entrata);

il termine $\gamma i$ dà invece la variazione dei ritirati, come abbiamo appena considerato ( in uscita) quindi con segno negativo.

$\Delta i=(\beta si-\gamma i)\Delta t$ da cui otteniamo il rapporto incrementale seguente:

$\frac{\Delta i}{\Delta t}= \beta si - \gamma i$ e passando al limite, per $\Delta t\rightarrow 0$ , otteniamo l'ultima equazione differenziale:

$\frac{di}{dt}=lim_{\Delta t\rightarrow 0}\frac{\Delta i}{\Delta t}= \beta si - \gamma i$

Sommiamo ora le tre equazioni ricavate :

Questo conferma che la somma s+i+r è costante nel tempo e, date le condizioni iniziali, è pari a 1.

Analizziamo per prima cosa le condizioni iniziali .

Possiamo supporre senz'altro:

Cioè, al tempo 0 avremo un certo numero di superati $S_{0}$ , e potremmo avere anche di già un certo numero di istruiti, $I_{0}$ . Solo i ritirati , $R_{0}$ , possono essere eventualmente anche uguali a zero.

riprendiamo le tre equazioni differenziali:

Dalla prima equazione , essendo $\beta ,s,i$ quantità positive, $\frac{ds}{dt}<0$ , deduciamo di conseguenza che s(t) è un funzione decrescente .

Risulta quindi, che per t tendente a infinito , $lim_{t\rightarrow \infty}S(t) =S_{\infty}$ che prende il nome di dimensione del processo..

Questo ci fa pensare che , diventando costante al limite S(t), I(t) debba tendere necessariamente a zero. E infatti è proprio così.

$lim_{t\rightarrow \infty}I(t) =0$ *;

e quindi gli I (istruiti) sono destinati ad estinguersi. Questo in ogni caso.

Essendo s(t) + i(t) + r(t) = 1 (o analogamente S(t) + I(t) + R(t)=N), possiamo limitarci a studiare solo le due equazioni:

e se necessario, ricavare i risultati per R(t) da R(t)=1-S(t)-R(t).

Anche nel modello SIR è presente il fenomeno di soglia. Infatti, posto $T=\gamma /\beta$ , possono ottenersi i seguenti due casi:

Se S₀<T, allora è facile provare che per ogni t>0

$S(t)<T\Rightarrow \frac{dI}{dt}<0$

Infatti $\frac{dI}{dt}=N\frac{di}{dt}=N(\beta si-\gamma i)$

$S(t)<T\Rightarrow s<\frac{T}{N}$ ;

$T/N=\frac{\gamma }{\beta N}$

$\frac{dI}{dt}<N(\beta \frac{\gamma }{N\beta }i-\gamma i)=0$

In questo caso, il procedimento di tipo "epidemico" non si innesca ed il numero di istruiti decresce dal valore iniziale I0 fino ad annullarsi.

Se S₀>T, allora solo inizialmente il numero di infetti cresce, cioè risulta

$\frac{dI}{dt}|_{t=0}>0$ (questa scrittura significa che calcoliamo la derivata nel punto t=0.

e quindi il processo di apprendimento inizialmente si sviluppa, la funzione I(t) raggiunge un valore massimo I_max e poi decresce fino a zero.

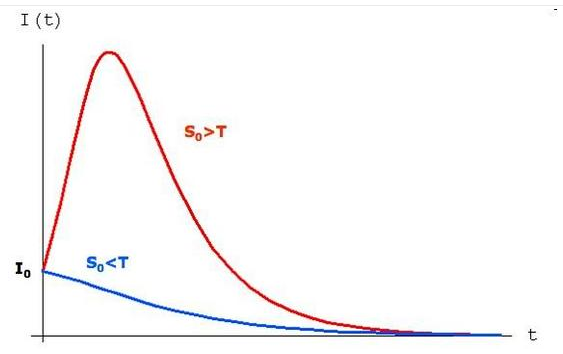Nella figura, è evidenziato il fenomeno soglia.

Ma veniamo ai calcoli; vogliamo stimare sia la percentuale della popolazione che sarà trasformata , $S_{\infty}$ che quella massima istruita I_max/N e poi in decadimento. Dalle prime due equazioni

dividendo membro a membro si ricava:

$\frac{dI}{ds}=-1+\frac{\gamma }{\beta S}$

che integrata con il consueto metodo di separazione delle variabili, ci dà:

$I(S)=c_{0}-S+\frac{\gamma }{\beta }\ln S$ **

[ al solito; $\frac{dI}{ds}=-1+\frac{\gamma }{\beta S}$ , $dI=(-1+\frac{\gamma }{\beta S})ds$ , $I=\int (-1+\frac{\gamma }{\beta S})ds +c_{0}$ ,

$I(S)=c_{0}-S+\frac{\gamma }{\beta }\ln S$ ]

dove $c_{0}=I_{0}-S_{0}-\frac{\gamma }{\beta }\ln S_{0}$ (basta infatti sostituire a t il valore 0 in **.

Ricordando che $I(t)\rightarrow 0$ per $t\rightarrow \infty$ , dalla ** si ottiene che $S_{\infty}$ è soluzione alla seguente equazione

$c_{0}-S_{\infty}+\frac{\gamma }{\beta }lnS_{\infty}=0$ .

Analogamente, notando che I_max si ottiene in corrispondenza del valore $S=\gamma /\beta$ , dalla ** si ricava

$I_{max}=(I_{0}+S_{0}-\frac{\gamma }{\beta }lnS_{0})-\frac{\gamma }{\beta }ln(\frac{\gamma }{\beta })$

(infatti basta fare la derivata della ** ; e vedere dove si annulla; $\frac{d}{ds}I(S)=\frac{d}{ds}(c_{0}-S+\frac{\gamma }{\beta }\ln S)=-1+\frac{\gamma }{\beta S}$ ;

ma $-1+\frac{\gamma }{\beta S}=0$ quando $S=\gamma /\beta$ )

L	M	M	G	V	S	D
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

Ancora un modello matematico:Il SIR *** (di Maurizio e Umberto)

Articoli correlati

(Q) Un semplice esponente ... **

Soluzioni dello scontro evitato **/***

Evitiamo uno scontro **/***

Il Problema di Apollonio e le "sue" coniche. 4 ***

Lascia un commento Cancel Reply

Soluzioni dello scontro evitato /*

Evitiamo uno scontro /*