Parlare di barche, navi e della loro stabilità sia con mare calmo che agitato comporterebbe un intero libro (e magari nemmeno basterebbe). Tuttavia, dato che, comunque, una nave galleggia per effetto del Teorema di Archimede non possiamo esimerci dal dare qualche informazione di base a riguardo.

Sicuramente, le navi di oggi hanno forme ben diverse dal tronco a sezione quadrata che abbiamo utilizzato fino ad ora. Tuttavia, i punti essenziali rimangono sempre il baricentro del corpo che galleggia e il punto di applicazione della spinta verso l'alto. In particolare, la loro distanza sia in verticale che in orizzontale. La famosa coppia che creava situazioni più o meno paradossali nel tronco, diventa adesso un requisito fondamentale per far tornare la nostra imbarcazione in equilibrio, ossia con il ponte parallelo alla superficie liquida. Chi adesso sposterà la condizione ideale con i due punti perfettamente in verticale sarà soprattutto il moto ondoso o il vento. A volte, però, è proprio una configurazione non ideale quella che permette di sfruttare al massimo il vento per andare più veloci e quindi si dovrà anche essere pronti a cambiare il baricentro totale in modo artificiale. In poche parole, ad ogni barca il suo equilibrio...

Iniziamo con un discorso estremamente generale e semplificato.

Immaginiamo che a causa di un piegamento della nostra barca-galleggiante la verticale passante per il baricentro A della parte sommersa (dove possiamo applicare la spinta di Archimede) e quella passante per il baricentro G totale del corpo non siano più coincidenti. In tal caso, come abbiamo visto precedentemente, si instaura una coppia che tende a far ruotare l'intero scafo. Questa coppia può, ovviamente, o far ribaltare lo scafo (beato chi sa nuotare!) oppure far ritornare il tutto nelle condizioni iniziali (baricentro A e baricentro G perfettamente allineati sulla verticale).

Immaginiamo, ancora, che il baricentro G stia sempre sulla linea di simmetria dell'imbarcazione (è difficile vedere una nave che ha la parte destra diversa dalla parte sinistra, ma a volte può capitare...). Possiamo allora tracciare un semplice schema (senza nemmeno disegnare il natante) che poi applicheremo ad alcuni tipi di  vascelli reali. La superficie del mare è sempre disegnata in orizzontale, ma, se la nave si piega, non è più orizzontale la linea di simmetria, dove imponiamo che stia il baricentro G. Non sappiamo la posizione esatta, ma sappiamo che deve stare sulla linea s. Sia invece A il baricentro della parte sommersa e immaginiamolo fissato. La  perpendicolare alla superficie passante per A indica la direzione della spinta verso l'alto, la perpendicolare alla superficie tracciata da G indica, invece, la direzione della forza peso del natante. Consideriamo perciò la Fig. 12.

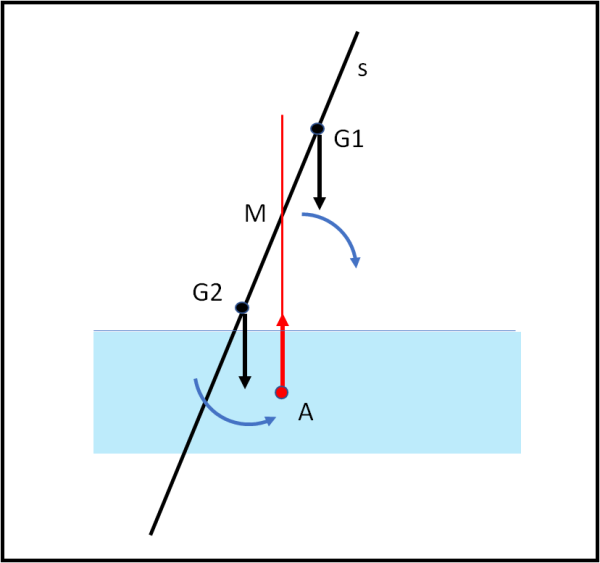
E' immediato concludere che se il baricentro della barca fosse in G1 la coppia risultante tenerebbe a far ribaltare l'imbarcazione, mentre se il baricentro fosse in G2 la barca si raddrizzerebbe. In questa semplice configurazione si vede subito che esiste un punto particolare, indicato con M, tale che se il baricentro G sta più alto di lui la nave affonda, se sta più in basso la nave si rimette in condizioni normali. Questo punto è chiamato METACENTRO ed è fondamentale per progettare le navi. Esso è definito come l'intersezione tra l'asse di simmetria s del natante e la verticale tracciata dal baricentro della parte sommersa. Si chiama altezza metacentrica la distanza (con segno) tra M e il baricentro G. Se essa è maggiore di 0, l'equilibrio è stabile; se essa è minore di 0, l'equilibrio è instabile, se è proprio uguale a 0, l'equilibrio è indifferente.

Capiamo subito che esistono alcuni parametri fondamentali se vogliamo costruire una barca o addirittura una nave: scegliere la giusta densità  affinché il baricentro sia abbastanza basso e disegnare una  forma in modo che, nelle condizioni favorevoli di metacentro, sia massima la coppia raddrizzante. In poche parole contano proprio la distanza tra le due forze della coppia, così come la distanza in verticale tra i due baricentri. E poi ci sono mille sfumature a seconda di come si vuole navigare.

La Fig. 13 mostra una nave dalla forma abbastanza normale, che sta sbandando, ma che non ha problemi a rimettersi in linea.

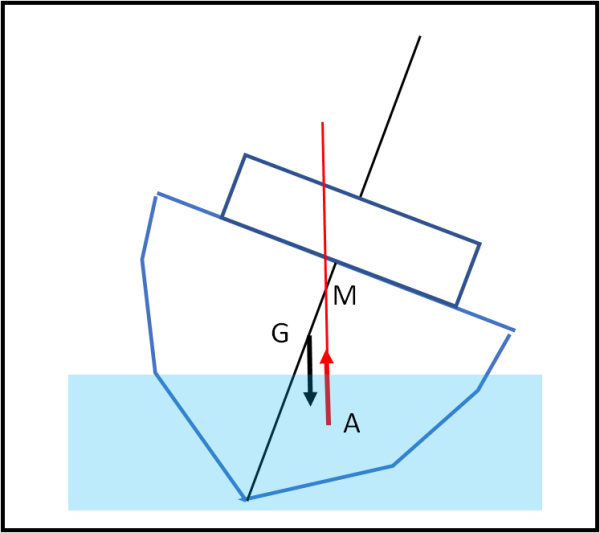
Innanzitutto, per potere galleggiare la nave non può essere troppo pesante, altrimenti raggiungerebbe l'equilibri solo toccando il fondo del mare. E non può nemmeno avere la stessa densità dell'acqua, altrimenti galleggerebbe, ma al di sotto della superficie marina (questa soluzione lasciamola ai sommergibili). Eppure le grandi navi sono fatte di metallo, decisamente più pesante dell'acqua. Beh... quello è l'involucro esterno... Anche l'uomo è fatto del 70% di acqua ma provate a dare un pugno nel torace dell'indimenticabile Cassius Clay- Mohamed Alì e vedrete che chi soffrirà molto sarà proprio la vostra mano. Ne segue che esternamente la nave è robustissima, ma internamente ha molti vuoti o cianfrusaglie varie più leggere dell'acqua. In conclusione, la sua densità totale deve essere minore di quella dell'acqua. Questo fatto ci fa anche capire che giocando sulla forma, ossia il volume (ma non solo), si può abbastanza facilmente spostare il baricentro G lungo l'asse di simmetria.

Non vogliamo andare nel particolare, altrimenti non si finirebbe più e, poi, ci vorrebbe un vero ingegnere navale. Tocchiamo solo un paio di casi abbastanza comuni. Prendiamo una bella barca a vela che deve sfruttare molto il vento per andare veloce. Essa deve anche subire notevoli oscillazioni, avendo, oltretutto, un baricentro variabile dato dalla posizione della vela. E' fondamentale, in questo caso, che il baricentro della barca sia molto basso, in modo da essere sicuri di riprendere l'assetto parallelo alla superficie marina e non capovolgersi del tutto. Bene, basta mettere un bel pezzo di ferro pesante sotto la chiglia: sarà lui a comandare il baricentro, che permetterà di avere un metacentro sempre sopra di lui (Fig. 14)

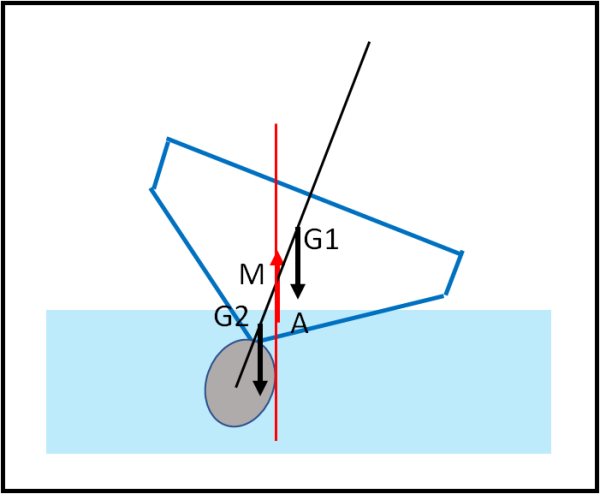
Il baricentro G1 farebbe ribaltare la barca, ma l'aggiunta del peso sotto la chiglia lo porta in G2, molto più in basso.

In casi disperati basta che i marinai aiutino lo spostamento del baricentro, come nell'immagine che segue.

Nel caso precedente abbiamo sfruttato l'altezza del baricentro totale, ma potremmo anche sfruttare la distanza tra le due linee verticali, come, ad esempio viene fatto per il catamarano (Fig. 15).

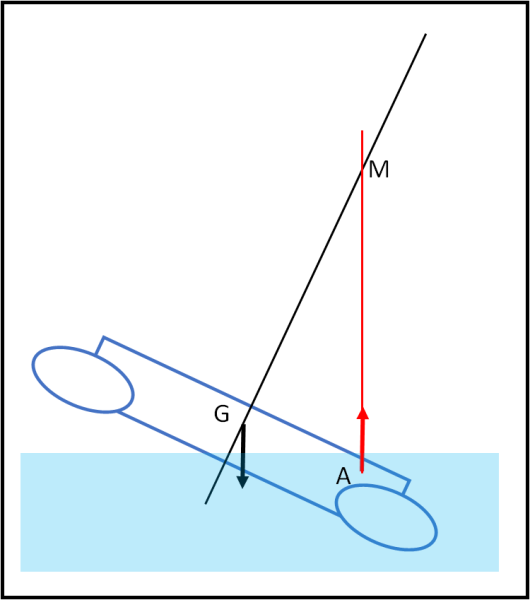
Anche in questo caso l'aiuto del marinaio può essere fondamentale, come mostra la figura che segue

Bene, scusate i disegni decisamente rozzi e brutti, ma ho poca dimestichezza con barche, navi e imbarcazioni varie...

Concludiamo qui il nostro breve "corso" sul teorema di Archimede, rimandando magari a un'altra volta un discorso più articolato, con l'aiuto indispensabile di un ingegnere o, magari, anche solo di un bravo marinaio!

Gli altri articoli dedicati al Teorema di Archimede li trovate QUI