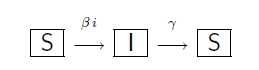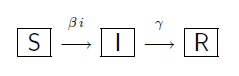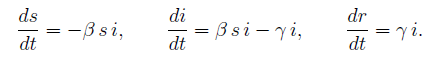Riassunto dei modelli SI,SIS,SIR.***(di Umberto e Maurizio)

Categorie: Matematica Tags: modelli matematici Scritto da: Umberto Cibien Commenti:0

Questo articolo contiene una panoramica dei tre modelli matematici trattati, applicabili ad eventi che riguardano "cose" che si trasmettono con il contatto tra individui di una popolazione.

N.B.: per i dettagli , vi rimando al tag modelli matematici dove trovate per esteso tutti i calcoli.

Sostanzialmente , tutto si basa principalmente sulla formula, giustificata sia statisticamente che empiricamente:

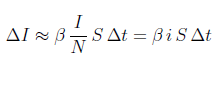
Assieme alla costanza della popolazione, ovvero i/(t)+ s(t)=1, indicata in percentuale rispetto a N, totale popolazione. Consideriamo cioè la popolazione come un sistema chiuso; nessuno entra od esce. Il coefficiente $\beta$ è alla base di tutto. La variazione dei nuovi soggetti I porta è proporzionale al tempo, al numero dei soggetti non ancora trasformati S e alla percentuale dei soggetti i stessi. Come già detto in precedenza, Il coefficiente può essere interpretato come il numero medio di contatti a persona sufficienti per la trasmissione per unità di tempo.

Chiaramente i, s variano in continuazione allo scorrere del tempo t; perciò siamo costretti a ricorrere alle equazioni differenziali per risolvere analiticamente il problema.

Ci sono state tre varianti nei modelli analizzati

1. Il modello SI

Il modello SI in cui abbiamo a che fare solo con soggetti del tipo S e I e in cui non esiste reversibilità, ovvero un soggetto S passa alla classe I e lì vi rimane.

le equazioni differenziali:

e la costanza della popolazione,

Ci hanno permesso il calcolo delle funzioni analitiche S,I in funzione di t:

$S(t)=\frac{NS_{0}}{S_{0}+I_{0}e^{\beta t}}$ ,

$I(t)=\frac{N\cdot I_{0}e^{\beta t}}{S_{0}+I_{0}e^{\beta t}}$

Per studiare il comportamento asintotico , bisogna studiare i limiti di queste due funzioni per $t\rightarrow \infty$ ;

Vediamo subito che:

S(t)--->0

I(t)---> N

La cosa che interessa di più è la curva cosiddetta epidemica, cioè la curva che associa al tempo t, il tasso di crescita della trasformazione degli Sprovveduti in Istruiti:

$\frac{di}{dt}(t)=\frac{\beta N^{2}S_{0}I_{0}e^{\beta t}}{(s_{0}+i_{0}e^{\beta t})^{2}}=\frac{\beta s_{0}i_{0}e^{\beta t}}{(s_{0}+i_{0}e^{\beta t})^{2}}$
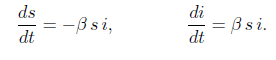
Essa si ottiene derivando la funzione I(t). rispetto al tempo (cosa che lasciamo ai più volenterosi)
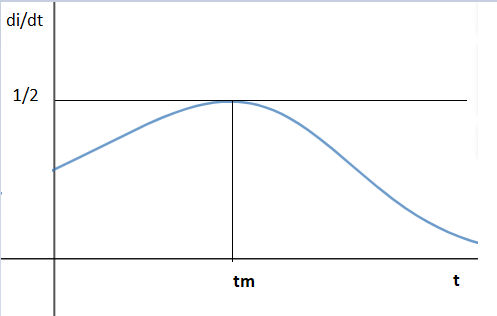
Ma in quale istante si raggiungerà la massima conversione degli Sprovveduti in Istruiti ?
Studiando la funzione (cercasi volenteroso), si ottiene che essa presenta un massimo, il cosiddetto valore di picco, per il valore di tempo:

$t_{M}=ln(\frac{s_{0}}{i_{0}})/\beta$

nel qual caso si ha:

$s(t_{M})=i(t_{M})=\frac{1}{2}$

Faccio notare che la curva I è una curva asintotica, che tende a N:

mentre invece, la curva delle variazioni, che è quella che ha un picco , è la curva della derivata di/dt:

Guarda un po’ che strano... quando la metà della popolazione è stata trasformata da uno stato all’altro, proprio in questo preciso momento, inizia una sistemica difficoltà nel riuscire trasformare in Istruiti i restanti Sprovveduti. Le misure che diminuiscono i contatti chiaramente agiscono su $\beta$ , non risolvono il problema, ma danno tempo per affrontarlo.

2. Il modello SIS

Il modello SIS differisce dal modello SI per il fatto, che dopo un certo tempo i soggetti passati da S a I , ritornano nella classe S.

Schema grafico del modello:

Dove il coefficiente $1/\gamma$ esprime il tempo medio di ritorno alla classe dei superati,

In questo caso il sistema di equazioni differenziali è il seguente:

2222

Sappiamo, che dopo svariati calcoli, si arriva alle soluzioni per s,i:
.

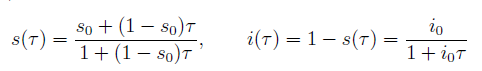dove è stato posto $\tau=\beta t$ . Posto $\sigma=\beta /\gamma$ , vogliamo studiare il comportamento asintotico di i(t) nei due casi, nei due casi, $\sigma \leq 1$ e $\sigma >1$ , che equivalgono ai casi, essendo $\sigma=\beta /\gamma$ , $\gamma >\beta$ e $\beta >\gamma$ ,

eq8

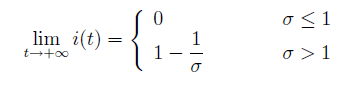
e , graficamente:

Per questo motivo $\sigma$ viene detto soglia critica per tale sistema, ed è il prodotto tra il tasso di contatto $\beta$ e il tempo medio di ritorno alla classe degli S, $1/\gamma$ . A secondo del suo valore si ha l'estinguersi del processo la sua propagazione a tutta la popolazione.

3. Il Modello SIR.

Introduciamo una nuova ipotesi che tenga conto di un fenomeno di “abbandono”. Vale a dire che, tra tutti coloro che periodicamente rientreranno nel circolo della formazione continua, vi saranno alcuni che abbandoneranno. Li individueremo con il termine R per Ritirati.

Schema grafico:

s + i + r = 1 sarà la nuova ripartizione delle rispettive percentuali degli stati possibili.

Le equazioni differenziale questa volta son tre,

Studiamo solo l'andamento delle soluzioni;

Anche nel modello SIR è presente il fenomeno di soglia. Infatti, posto $T=\gamma /\beta$ , possono ottenersi i seguenti due casi:

Se S₀<T, allora è facile provare che per ogni t>0

$S(t)<T\Rightarrow \frac{dI}{dt}<0$

Infatti $\frac{dI}{dt}=N\frac{di}{dt}=N(\beta si-\gamma i)$

$S(t)<T\Rightarrow s<\frac{T}{N}$ ;

$T/N=\frac{\gamma }{\beta N}$

$\frac{dI}{dt}<N(\beta \frac{\gamma }{N\beta }i-\gamma i)=0$

In questo caso, il procedimento di tipo "epidemico" non si innesca ed il numero di istruiti decresce dal valore iniziale I0 fino ad annullarsi.

2. Se S₀>T, allora solo inizialmente il numero di infetti cresce, cioè risulta

$\frac{dI}{dt}|_{t=0}>0$ (questa scrittura significa che calcoliamo la derivata nel punto t=0.

e quindi il processo di apprendimento inizialmente si sviluppa, la funzione I(t) raggiunge un valore massimo I_max e poi decresce fino a zero.

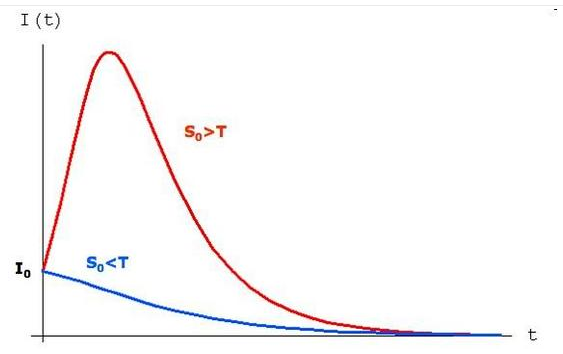Nella figura, è evidenziato il fenomeno soglia.

Riprendiamo ancora una volta i punti salienti dei tre casi, dal punto di vista grafico:

CASO SI:

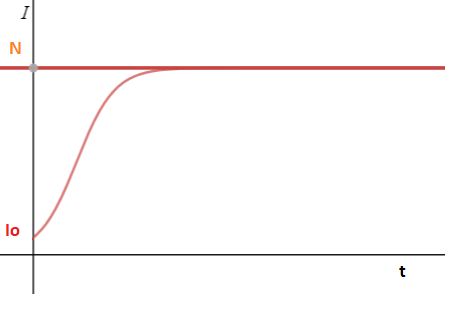
Il processo non si ferma, e tende a coprire tutta la popolazione:

Le variazioni degli I ha un massimo per i=s=1/2:

vsi

Caso SIS:

Decide l'evoluzione il parametro $\sigma$ che viene detto soglia critica per tale sistema ed è il prodotto tra il tasso di contatto $\beta$ e il tempo medio di ritorno alla classe degli S, $1/\gamma$ . A secondo del suo valore si ha l'estinguersi del processo la sua propagazione a tutta la popolazione.

CASO SIR

A seconda del valore si soglia, posto $T=\gamma /\beta$ , possono ottenersi i seguenti due casi:S₀<T, S₀<T:

A seconda dei due casi, o il processo decade rapidamente, oppure ha un picco elevato, però dopo il processo si estingue.

Teoria e applicazione

Non possiamo a questo punto astenerci da lanciare un monito: non illudetevi di poter navigare nella realtà a bordo di modelli "semplicemente didattici", come stanno facendo i troppi dilettanti allo sbaraglio in azione.

I fenomeni da considerare in un contesto reale sono molto più complicati e variegati di quelli descritti da semplificazioni estreme.

1. In un caso reale esistono sempre ambiguità nella classificazione dei dati sulle popolazioni e sulla reale consistenza numerica delle tipologie. Questo è un fattore critico per la qualità degli input incide massicciamente sui risultati.

2. Le ipotesi modellizzate sulle possibilità dei contatti devono essere molto più realistiche e articolate, rispetto alla grossolana semplificazione che ciascuno possa entrare in contatto con tutti gli altri. Occorre considerare leggi di distribuzioni e dispersione geografica e sociale, tempi, frequenze e probabilità dei contatti.

3. La efficacia di azioni di controllo sui parametri chiave (in particolare il coefficiente beta) nella realtà è molto più blanda che in teoria. Questo perché non si tratta di aprire o chiudere una valvola in un circuito, ma di valutare una tendenza collettiva, regolata da uno sterminato numero di scelte individuali, solo in parte prevedibili e influenzabili, a fronte di disposizioni che tendono ad orientare i comportamenti.

4. Tutti risultati ottenuti devono essere accompagnati da intervalli di confidenza che tengano conto almeno della propagazione degli errori sui dati in input, per non dire delle valutazioni di probabilità entro il modello.

Questo per citare solo alcune delle cautele necessarie manipolando questi modelli.

L	M	M	G	V	S	D
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

Riassunto dei modelli SI,SIS,SIR.***(di Umberto e Maurizio)

Articoli correlati

(Q) Un semplice esponente ... **

Soluzioni dello scontro evitato **/***

Evitiamo uno scontro **/***

Il Problema di Apollonio e le "sue" coniche. 4 ***

Lascia un commento Cancel Reply

Soluzioni dello scontro evitato /*

Evitiamo uno scontro /*