Categorie: Fisica classica Matematica Storia della Scienza
Tags: approssimazioni carta igienica quasiquiz Topologia
Scritto da: Vincenzo Zappalà
Commenti:57
La lezione della carta igienica, ovvero "il mondo andrà a ... rotoli?" */**/***/****
Quanto è lungo un rotolo di carta igienica?
Un problema che è tutto meno che facile. Sicuramente ha molti possibili metodi di approccio, più o meno approssimati. Non consideriamolo, quindi, come un quiz, ma come un impegno corale, in cui ognuno potrà inserire un mattone in più. Piano piano potremo costruire sempre meglio il nostro edificio e poco importa se sarà solo un rotolo di carta igienica.
Abbiamo anche una grande opportunità... possiamo sempre controllare il risultato migliore, passando alle maniere sbrigative: srotolare il rotolo di carta e misurarlo. Nessun problema a utilizzare anche un rotolo già iniziato, dato che le formule posso adattarsi a qualsiasi dato di partenza.
I dati di partenza, ossia i parametri noti e del tutto sufficienti, sono:
Raggio esterno del rotolo: R
Raggio interno del rotolo = raggio del cilindro di cartone su cui è avvolto: r
Spessore della carta: s
Ciò che vogliamo calcolare è decisamente semplice (a parole): la lunghezza L del rotolo di carta igienica.
Un problema che può toccare sia la geometria più o meno semplice, sia la matematica anche molto complicata, per non parlare anche della fisica classica e - perché no? - della topologia. In fondo, la topologia è una branca della matematica che descrive le proprietà di forme che cambiano solo a seconda di come sono disposte nello spazio, non nella loro forma o nelle loro dimensioni. Per esempio, si possono prendere in considerazione un rotolo di carta igienica e una ciambella. Esse hanno la stessa topologia, in quanto entrambi gli oggetti hanno un solo buco, nonostante possano avere dimensioni e forme diverse.
Uno spunto di "lavoro" che non vuole avere un termine temporale preciso. Lo lasceremo a "bagnomaria" sperando che un po' alla volta il numero di soluzioni proposte si allunghi un po' come la carta igienica di una nota casa di produzione, dal nome perfetto in questo periodo di virus "coronati"...
Un caso numerico a cui applicare le varie soluzioni:
r = 20 mm
R = 55 mm
s = 0.36 mm
Non pretendiamo un numero esatto, dato che i parametri sono stati determinati a ... rotolo chiuso. Sappiamo comunque il risultato.
P.S.: il risultato è stato ottenuto senza aver mai utilizzato il nostro strumento di indagine...
QUI una disamina di alcuni dei metodi utilizzabili per misurare il rotolo senza srotolarlo, oltre a qualche "pillola" sulla storia di una delle più grandi conquiste di civiltà!
Lasciatemi chiudere questa proposta con una canzone del grande Roberto Benigni, sperando che nessuno abbia di che storcere il naso: in fondo è un'operazione che ci accomuna tutti!
57 commenti
I metodi seri li lascio a quelli bravi, io mi accontento di calcolare con un discreto grado di approssimazione che il rotolo misura circa 23 metri (su Papalla abbiamo molto senso pratico
).
Non proprio dieci piani di morbidezza, ma circa otto (o no?!?)
Caro Papalscherzone.
Il tuo approccio non sarebbe affatto male. Due piccoli appunti. Innanzitutto dire che genere di approssimazione hai usato. Infatti, per fare la somma che ci hai fornito devi aver usato per forza un modello geometrico semplificato... SPECIFICALO PER BENE. Riguardo al risultato finale deve essere proprio 55 e non un po' di più o un po' di meno... Le differenze tra i vari approcci saranno minime e quindi non si può dare uno scarto così grande...
Mentre i lettori più matematici sono già al lavoro per scrivere ( e calcolare) l'integrale di linea che fornisce la lunghezza precisa dell'arco di spiralona che va dal nucleo allo strato più esterno, mentre l'alieno del circolo ha già prodotto un excellente risultato numerico, devo lanciare un atto di accusa nei confronti del perverso ideatore del quiz.
Sia i risultati approssimati, sia il risultato matematico che calcoleranno quelli bravi, costituiranno solo approssimazioni grossolane, tutte per difetto, della vera lunghezza. Le stesse case produttrici del prezioso articolo vi inducono in errore, per sporchi interessi di guadagno, parlando di 10 piani di morbidezza a vostra disposizione. La vera lunghezza è estremamente maggiore di quanto vi fanno credere.
Questo perché la carta crespata, anche la più fine, non ha dimensione di Hausdorff = 1.
Se è ambiguo chiedere qual è la lunghezza della costa dell'Inghilterra (Mandelbrot 1967), altrettanto subdolo - e degno solo di una mente diabolica come quella di Enzo - è chiedere la lunghezza della striscia di carta igienica , per giunta arrotolata.
La scabrosità della carta si annida con una regola di autosimilarità, a scale sempre più piccole, con conseguenze che Enzo non può negare di conoscere, e qui ne avete la prova inconfutabile: http://www.infinitoteatrodelcosmo.it/2019/08/04/soluzione-dellisola-non-ce-ovvero-fiocco-neve-koch/
Proprio così, il rotolo ha lunghezza infinita. Se, ad esempio, la rugosità è comparabile con quella della curva di Koch, la sua dimensione frattale è data dal rapporto ln 4/ln 3 = 1,2619 e la lunghezza è infinita (come ben sa il titolare del blog).
Solo la nostra superficialità ci porta a considerare la dimensione frattale=1, a credere che la carta finisca e che sia necessario ricomprare periodicamente pacconi e pacconi di rotoli. La conoscenza non è solo potere, è anche risparmio.
Mi spiego meglio...
Papalscherzone considera proprio a causa del suo approccio, che esista uno strato esterno di raggio uguale a 55. In realtà noi abbiamo misurato che lo spessore massimo è esattamente 55, ma non abbiamo detto che esiste realmente uno strato completo di raggio pari a 55. Noi ci fermiamo quando il raggio esterno tocca i 55....
Sì sì... sono perfettamente consapevole di tutte le approssimazioni che ho fatto e mi avvalgo del diritto papalliano di fermarmi qui.
Giustamente mi chiedi di spiegare meglio il grossolano ragionamento, ecco qua...
Le scritte in nero sono quelle da cui sono partito stamani prima di fare i calcoli con excel.
Le scritte in rosso le ho aggiunte ora e hanno la pretesa di rappresentare le 97,2 (2 periodico) circonferenze concentriche con cui ho approssimato gli strati la somma delle cui lunghezze si avvicina alla lunghezza reale del rotolo.
So benissimo che l'approssimazione è brutale in quanto non c'è alcun salto tra uno strato e l'altro, e che l'ultimo strato sicuramente non è completo, ma questo lo lascio fare a quelli più bravi di me, mentre io inizio a documentarmi sull'interessantissima storia della carta igienica! Lo sai, per esempio, che negli anni '30 del secolo scorso (dico... 90 anni fa, mica 900!), uno slogan pubblicitario ne vantava la "morbidezza" dicendo che era "priva di schegge"??
Caro Mau... non rompere!!! e vedi di partecipare attivamente, uffa!
Attenzione Papalscherzone: qual è la lunghezza di una striscia di raggio interno 2 e raggio esterno 3 (ossia spessa 1)? E' 2 pi 2 o 2 pi 3 ?
Facendo finta che la carta sia perfettamente liscia (ipotesi ripugnante , che la renderebbe ben poco efficace) e che la lunghezza sia calcolabile, la si può determinare in altri modi, senza il calcolo differenziale, ragionando sulle proprietà fisiche dell'oggetto.
Mi riservo di illustrare qualche esempio in seguito, ma prima lascerei intervenire i volenterosi lettori.
Io, invece, non mi riservo un bel niente e mi avvalgo pertinacemente della facoltà di approssimare di brutto e di non rispondere alle provocazioni.
Ho un appuntamento con la storia (della carta igienica) e non lo mancherò!!
scusa se faccio una precisazione ; quello che dici sulle form è vero, ma ovunque dove parliamo di problemi quantitativi la topologia non c'entra niente.
Buonasera Professore, mi scuso in anticipo per il commento non attinente all'articolo ma la settimana scorsa le ho inviato un messaggio con delle richieste di informazioni tramite la sezione apposita del sito per le comunicazioni, tuttavia temo che non lo abbia ricevuto. Le scrivo il mio indirizzo email in modo che magari possa recuperarlo, nel caso sia finito nella posta indesiderata: santothejolly@hotmail.com.
Nell'attesa di ricevere un suo cortese riscontro la saluto cordialmente.
Antonio Spanu
caro Mau,
due pensieri sul tuo appunto..
Temo di sì, Antonio...
Ovviamente Umberto, ma era tanto per estendere il caso delle forme.
caro Mau,
in realtà ci si può approssimare in vari modi. Ma esiste una formula abbastanza precisa. Anche se, come dicevo per potere essere precisi bisognerebbe tener conto di moltissimi particolari di tipo fisico. Inoltre, nell'esempio riportato, le misure sono state fatte a priori e quindi nessun problema aggiuntivo può essere stato tenuto in conto. Lo scopo è solo quello di applicare vari metodi alla determinazione di una lunghezza non misurabile direttamente.
Rispondo io alla domanda fatta a Papalscherzone...
La carta igienica, al primo giro, nell'ipotesi dei cerchi concentrici che considera Papalscherzone, deve coprire completamente la circonferenza del cilindro di cartone. Essa vale perciò 2πR1. Su questo non possiamo transigere: se fosse più lunga avremmo già fatto una piccola piega. Ma, lo spessore non è nullo e, quindi, eseguito il primo giro, anche la parte superiore della carta igienica deve avere percorso una lunghezza 2πR1. Ne risulta che ci manca un pezzetto per coprire un angolo di 360°, che sarebbe coperto totalmente da una circonferenza pari a 2πR2. Il pezzetto che manca è proprio uguale a R2 - R1, ossia lo spessore s. La stessa cosa capiterà per ogni strato successivo, Il che significa che la nostra misura è sempre minore della realtà. L'approssimazione rimane buona, per difetto, solo per s << R.
Tanto per non creare subito confusione...
Caro Enzo, stavo giusto mettendo a punto approcci sperimentali alternativi , a quelli che ipotizzi, che conoscerai nei prossimi giorni. Ma veniamo ai tuoi commenti....
Innanzi tutto sappi che il rotolo "reale" di lunghezza infinita, consente un uso ottimo/abbondante del materiale, che una, volta usato, viene avviato tramite la consueta procedura, al suo ineluttabile destino fognario. Per tua tranquillità sappi che la lunghezza restante continua ad essere sia infinita sia pulita.
Sono certo che, dopo un breve tirocinio (... non ci sono inviti sottintesi) saprai trarre anche tu giovamento da questa informazione.
Per quanto riguarda gli anelli concentrici di Scherzy, si può fare qualche riflessione come segue...
si calcola la lunghezza complessiva di N cerchi concentrici, di raggi crescenti progressivamente in ragione dello spessore S.
Lunghezza complessiva = N * circonferenza media = N * 2 pi* (Rmax+Rmin)/2= N *pi*(Rmax + Rmin)
Caro Maurizio,
cerchiamo di non dire troppe cose senza uno schema ben chiaro. Si rischia di confondere i lettori... Finora l'unico approccio che mi è giunto è quello di Dany, in cui vi erano due problemi: 1) non è possibile creare un anello che circondi il rotolo centrale. 2) considerando come raggio quello esterno si compie un errore che diventa molto "grande", alla fine.
Tuttavia, l'approccio è giustificato se si considera come raggio di ogni anello quello interno, perdendo un pezzetto alla volta. Come tale va considerato e vorrei avere la lunghezza che deriva da questo approccio che chiamerei il numero (1). Un approccio del tutto giustificato per s << r
Se tu vuoi proporne uno nuovo o sei vuoi migliorare quello di Dany, ti pregherei di essere più chiaro, partendo dal concetto base e spigandolo in modo elementare. Lo chiameremo approccio (2).
Non dobbiamo, comunque, mischiare realtà e approcci a scatola chiusa (a rotolo chiuso). Questi ultimi, che sono quelli che vuole il problema, sono giocoforza teorici e, quindi, vanno presi come tentativi di prevedere la realtà. Se volessimo la lunghezza ultra esatta avrei chiesto di srotolare il rotolo e buona notte!
Il vero scopo non è quello di prevedere la prossima andata al supermarket per fare rifornimento e nemmeno quella di dire che la carta è infinita e quindi tenersi quella di 50 anni fa, dato che -guarda caso- a me finisce sempre. Lo scopo è di usare sistemi con un minimo di formule (più o meno complesse) per avvicinarsi al massimo alla realtà, in modo tale da utilizzare e ricordare o implementare vari sistemi di calcolo che sono già stati usati... Un caso pratico (più o meno) per fare un bel ripasso...
Se lo spazio dei commenti è troppo piccolo e noioso da riempire, si può sempre farne un sunto ridotto e mandarmi la soluzione completa, scritta in modo divulgativo, via email, che io inserirò di volta in volta in un articolo dedicato alle risposte.
Grazie a tutti per l'aiuto nel cercare di coinvolgere il massimo numero di persone,,,
Non capisco perchè 55 metri. Ho fatto i conti in due modi diversi. Oppure ho capito male? In effetti io calcolo una lunghezza più piccola, ma non dimezzata. E' vero che bisognerebbe tener conto di questo fatto:
cioè dell'allungamento sul salto scalino, ma non può produrre differenze così grandi, Sono certo che avrai fatto bene i conti, ma proprio non capisco. Io li ho fatto semplicemente con i volumi unitari, ma anche con la sommatoria dei fogli che aumentano progressivamente. Boh.
scusa Umberto... ma chi ha mai parlato di 55 metri? 55 mm è il raggio del rotolo esterno... Ti stai confondendo tra raggio e lunghezza?
Per Umberto:
In realtà, poi, lo scalino non esisterà veramente, dato che la carta non rimane appiccicata fino a poco prima dello scalino...
Per Mau...
quel tratto aggiuntivo mi convince poco e non capisco come venga fuori: la circonferenza del primo strato (quella a contatto con il tubo) è proprio della lunghezza giusta, ossia 2 pi R1. Tu la consideri più lunga in modo da farla girare verso l'alto... ma poi il raccordo non mi sembra tanto ben spiegato. Forse ho capito cosa intendi, ma dovresti spiegarti meglio facendo magari delle freccette per far vedere il vero andamento della carta che tu consideri nel tuo approccio. Questo sarebbe comunque un approccio diverso da quello di Dany...
PER ADESSO I COMMENTI SEMBRANO FUNZIONARE. IL VERO PROBLEMA E' ENTRARE NEL CIRCOLO E SCRIVERE ARTICOLI...
ok, ma perchè a me viene circa 23 metri e a te 55?
scusa si sono intrecciati i commenti. avevo capito che avevi detto a Daniela che era 55 m il risultato.
Io ho usato i volumi, mi sembra in definitiva il conto più semplice. Se consideriamo il cilindro di altezza h,
La differenza fra i volumi dei due cilindri di raggio r e R e altezza h è uguale al volume del parallelepipedo di lunghezza L, altezza h e larghezza s; quindi:
che sostituendo i valori dà 22.895; Mi sembra il metodo più semplice e immediato. Bisognerebbe tener conto del gap generato dallo scalino, che potremmo assumere uguale allo spessore, e moltiplicarlo per il numero di fogli che compongono il rotolo, N=(R-r)/s e aggiungerlo. Forse tu avrai qualcosa di più sofisticato..
Ottimo Umberto,
questo è l'approccio che avevo pensato anche io come il più sbrigativo e fisico. In fondo, non è altro che la conservazione della massa ...
Ed è il numero (2)
Scusa Umberto... a me, però, viene 22907 ...
(552 - 202)π/0.36 = 22907,4464 (teniamo i decimali perché potrebbe essere importante...).
Secondo me non esiste problema scalino vero e proprio, dato che ogni foglio si adagia su quello sottostante, tranne che nel primo giro...
Caro Vincenzo, non ti sarà sfuggito il fatto che la lunghezza trovata da Umberto 22,895 metri, coincide esattamente con quella che avevo trovato io stesso nel precedente commento.
Con vie diverse, abbiamo espresso il concetto che tutto il volume compreso tra circonferenza esterna e interna del rotolo è occupato dalla striscia di carta.
Ripropongo il mio disegno corredato dalle frecce, come suggerivi, assieme alle formule che avevo scritto, con qualche passaggio in più.
Numero di cerchi concentrici N = (R esterno - R interno)/S = (55-20)/0,36 = 97,(2)
raggio della circonferenza media R medio = R interno+R esterno /2 = (55+20)/2 = 37,5 mm
lunghezza circonferenza media C media = R medio*2 pi = 37,5*6,28 = 235,5 mm
Lunghezza totale della striscia L = N* C media = 97(2) *235,5 = 22895,8(3) metri (approssimato a 22.895 metri)
Chiamiamo pure modello 2 questa schematizzazione. In essa ogni spazio è occupato dalla striscia di carta.
Ma il passaggio del gradino tra uno strato e l'altro, come anche Umberto aveva rappresentato in una figura, può avvenire in modo più raccordato. In questa
figura si vedono in sovra impressione i due possibili percorsi nel saltare il gradino.
Non tutto il volume , in questo caso, sarà occupato dalla carta.
Se chiamiamo questo schema Modello 3, è intuitivo che la lunghezza che troveremo sarà inferiore.
Il percorso lungo linea tangente alla circonferenza di raggio R1 che giunge al livello superiore (raggio R2= R1+s) è più breve del percorso che sale verticalmente da R1 a R2 (l'ipotenusa è più piccola della somma dei cateti).
Avendo la misura dello spessore si può calcolare l'angolo alfa
alfa = arcos R1/ (R1+S)
La lunghezza dell'arco corrispondente A= R1* (alfa*pi/180)
Invece di seguire quell'arco, la striscia si disporrà lungo la linea di raccordo tangenziale che avrà lunghezza T = R1 sen(alfa).
La lunghezza dell'anello di raggio R1, così deformato sarà: L1= 2 pi R1 - A +T
La riduzione di lunghezza rispetto allo schema 2 è data dal rapporto:
K = ( 2 pi R1 - A -T ) / 2 pi R1
Dato che la deformazione si riproduce su tutti gli anelli concentrici, questo rapporto vale anche a livello globale. La lunghezza totale sarà
L= 22.895 * K
Passando ai valori dell'esempio: R1= 20 mm S=0,36 mm
alfa = arcos ( 20 / 20,36) = 10,79°
A= 20*(10,79*3,14/180) =3,76 mm
T=20*sen(10,79) = 3,74 mm
L1=2*3,14*20 - 3,76 + 3,74 = 125,6 - 3,76 + 3,74 = 125,58 mm
K= 125,58/125,6 = 0,99984
Lunghezza totale = 22.895 * 0,99984 = 22.891,3 metri ( 3,7 millimetri in meno)
La differenza tra il tuo calcolo, Enzo, e quello di Umberto, sta nel fatto che lui ha utilizzato per pi il valore 3,14 mentre tu avrai utilizzato un valore con più decimali, come 3,1415926 o addirittura
3,1415926491428571428571428571429
si, penso anche io. Ho usato 3,14. Ho però un altro metodo, che si fonda sulle sommatorie dei fogli di raggio incrementale. Proverò il calcolo con essi
L'altra formula che ho ricavato , e di cui per adesso ometto i calcoli, si basa sul fatto che N=(R-r)/s è il numero di incrementi che subisce il raggio; quindi bisogna sommare le lunghezze di N circonferenze con raggio crescente dallo spessore, ovvero 2 π( r + sk ) dove k varia da 1 a N; usando la formula di Gauss si arriva al risultato:
strano, dovrebbe dare lo stesso valore dell'altro metodo , 22.895 . Ci devo ragionare.
In entrambi i casi, però, viene assunto che quasi tutto il primo giro sia perfettamente a contatto con il tubo interno. In realtà, è proprio così? Io penso che la carta, per fare l'inevitabile PRIMO scalino (quelli dopo non avranno problemi), sceglierà la via più diretta. O sbaglio? In altre parole e teoricamente: siamo sicuri che non rimanga sempre il primo salto di scalino vuoto?
D'accordo sul pigreco. Tuttavia, dato che le differenze saranno molto piccole, cerchiamo di usare tutti lo stesso valore di pigreco.
Scegliamo ad esempio: 3.1416
Volevo inserire una figura, ma non riesco...
Cerco di dirlo a "voce":
immaginiamo di voler mettere un tappeto su per una rampa inclinata che però inizia con uno scalino. Il tappeto parte prima dello scalino e lì viene incollato. Per tutta la rampa il tappeto aderisce perfettamente, però dal punto di attacco all'inizio della rampa rimane sospeso, cercando la linea di minor percorso. L'altezza della rampa è proprio R - r, mentre L è la lunghezza del tappeto. Finora, abbiamo cercato di far aderire il tappeto anche allo scalino facendolo andare orizzontale e lungo l'altezza dello scalino e poi via sulla rampa. Ma la carta igienica come si comporta?
Ma nello schema 3, c'è l'ipotesi che la carta non aderisca allo scalino ma vi arrivi con un piano inclinato, lasciando un po' di vuoto sotto. Tutti gli strati sovrapposti seguono questa deformazione del cerchio.
Dai calcoli mi risultava una lunghezza totale leggermente più piccola, ossia il 99,984 % di quella senza raccordo inclinato.
Rifacendo i calcoli con pi = 3,1416 ....
schema 2 L = 22.907,5 m
schema 3 L = 22.907,5 * 0,99984 = 22.903,8 m ( 3,7 mm in meno)
Non è una deformazione del cerchio, in realtà E poi nel caso dello scalino, il tappeto si stacca subito dopo la partenza... perché dovrebbe coincidere per un pò ???
Ho immaginato che la carta venga avvolta con una certa tensione che la tiene aderente al nucleo fino a quando incontra lo scalino. A questo punto , restando tesa , si assesta su una linea che è tangente al nucleo di cartoncino e tocca il bordo di inizio del nastro, appunto dove c'è lo scalino. Il punto di tangenza è individuato (vedi precedente commento sullo schema del modello 3). Tra il punto di tangenza e lo scalino resta uno spazio pieno di aria. La forma del primo giro non è un cerchio perfetto ma si chiude con quel segmento di lunghezza calcolabile.
Il giro successivo aderisce perfettamente e mantiene la forma distorta. E così tutti gli altri giri (omotetici)
perfettamente d'accordo, tranne il fatto che io direi che non si attacca mai...
la curva c'è ma non si vede... a me non piacciono le funzioni a gradino o a quasi-gradino... Ho provato con un telo e mi dà ragione...
Ti viene così? Perché questo è proprio lo schema 3.....
e io continuo ad essere convinto che, in modo impercettibile, la carta inizia a scostarsi dal cilindro fin dall'inizio. Così come fa il tappeto prima del gradino... Ci vorrebbe una vera prova, ma con le misure del nostro caso...
Insomma, il tuo approccio mi sembra troppo empirico...
Quello che proponi è sostanzialmente una molla a spirale, come quella di un orologio. Ma la carta si comporta diversamente da un nastro metallico. Sottoposta alla tensione si avvolge (e in realtà si allunga pure) aderendo fin dove è possibile al nucleo cilindrico sottostante. Solo dal punto di tangenza e fino allo spigolo del gradino si solleva dalla superficie di appoggio.
Pensa alla aderenza che si manifesta tra una puleggia e la relativa cinghia. oppure a come si dispone un filo di rame in una bobina di un trasformatore, o al filo di uno yoyo... c'è sempre un contatto.
Se guardi come è fatto il rotolo noterai che la striscia è in realtà incollata per tutto il primo giro.
Ma anche senza colla il nastro di carta, fissato nel punto iniziale, si comporterebbe come un elastico teso sulla superficie cilindrica del nucleo, assestandosi lungo la geodetica fino ad essere in prossimità del gradino.
La tensione della carta è proprio uno dei parametri del processo produttivo.
?
Sì, Umberto, questo è proprio quello che immagino che succeda nella realtà
boh... il nostro voleva essere un esercizio di matematica... sarà ma a me non piace per niente...
ingegneri... puff puff...
Possiamo sempre trovare un accordo... diciamo che una bella spirale di Archimede ( che Dio lo benedica) può rappresentare una buona approssimazione della curva reale, giusto per fare i conti più comodamente.
Oh bastalà, sempre sotto, questi scienziati !
Qui a Cuneo si è discusso a lungo sulla diatriba, davanti a una bottiglia di Nebbiolo d'Alba.
Quando era quasi finita, ( la bottiglia) un amico del "circolo archeofilo" salta fuori a dire: "E, se provassimo ad utilizzare un metodo basato sulle leggi della fisica? Qui nel testo del quiz si dice :
Un problema che può toccare sia la geometria più o meno semplice, sia la matematica anche molto complicata, per non parlare anche della fisica classica...
Dai, Oreste, facci sognare...
Allora, per farli contenti, ho preparato questo postino..
__________________________________________________________________
Quando Galileo si propose di studiare la cicloide, avendo difficoltà a misurarne per via teorica l'area, la riscontrò per via fisica, pesando materialmente dei pezzi di metallo ritagliati secondo la sagoma della curva e della circonferenza generatrice.
Galileo dedusse, così, per via empirica, che il rapporto doveva essere prossimo a 3:1 , ma rifiutò la sua prima intuizione, forse ritenendo tale rapporto troppo semplice. In realtà venne poi dimostrato rigorosamente che quel risultato era esatto.
Questa cosa è detta con parole più scientifiche anche qui : https://it.wikipedia.org/wiki/Cicloide
L'idea non è male, quindi... come trovare la lunghezza del rotolo con una bilancia?
Materiale occorrente una o due bilance, forbici
Possiamo pesare il rotolo (estraendo prima il nucleo di cartoncino) e troveremo il peso = P totale
Poi tagliamo con le forbici una striscia di lunghezza nota, esempio 1 metro e pesiamo anche lei, trovando il peso = P metro
La lunghezza in metri dell'intero rotolo vale L = peso totale/peso metro
Se la sensibilità della vostra bilancia non è sufficiente a pesare la striscia di un metro, leggete questo articolo
e realizzatevi la bilancia descritta che potrà servire anche ad altri utili scopi, per esempio sapere quanto pesa una mosca.
http://www.infinitoteatrodelcosmo.it/2018/12/31/giochiamo-nostri-bambini-la-costruiamo-questa-bilancia/
Se qualcuno pensa che, invece di costruire la bilancia, sia più semplice appallottolare la striscia di un metro , appendere lo sferoide di carta a un filo per realizzare un pendolo, misurare il periodo del pendolo e ricavare la massa, gli ricordo che il periodo del pendolo non dipende per niente dalla massa.
Dimenticavo... forse ho fatto male a spacchettare il rotolo, denuclearizzarlo e anche a tagliarne spudoratamente un metro di striscia per pesarla. Tuttavia dopo ho rimesso tutto a posto ed è come nuovo.
Cerea.
In realtà, sarebbe VIETATO strappare un metro di carta (è un nuovo dato di input), però va bene lo stesso, visto che l'ha proposto uno castenzato di Cuneo (scienziato delle castagne). Comunque, la fisica era già stata rappresentata dalla conservazione della massa...
Ma... a quando qualche bell'integrale???
Il metodo del peso è stato usato proprio da Archimede per le sue dimostrazioni, quindi è valido. Però non importa pesare, in quanto la lunghezza è sicuramente proporzionale alla superficie laterale del toro diviso l'ampiezza dello strato, che è un po' superiore a 0,36 per la presenza di aria ( e questo è un dato mancante). In ogni caso direi che:
L= pigreco (R^2 - r^2) / s
cioè meno di 22,9 m .
I dati del problema sono : R=55 r=20 s=0,36 pi= 31,1416 ( convenzione proposta da Enzo nel commento)
Inserendo questi dati nella espressione proposta da Leandro si ottiene:
L = 3,1416 * (55^2 - 20^2)/ 0,36 = 3,1416* ( 3025 - 400)/0,36 =3,1416*2625/0,36= 22.907,5
Un risultato che coincide esattamente con quelli trovati in precedenza nei diversi commenti.
Probabilmente, Leandro, hai utilizzato per pigreco il valore 3,14
In tal caso, infatti, il risultato è 3,14*2625/0,36 = 22.895,8 inferiore a 22,9 m e coincidente con i risultati già enunciati quando è stato usato anche dagli altri il valore 3,14.
Non è un caso che ci siano queste coincidenze, perché il modello usato è il medesimo, con aderenza del nastro di carta al nucleo centrale per tutto il primo giro.
Un diverso risultato si otterrebbe con un modello in cui il distacco dal nucleo inizia immediatamente e si amplia progressivamente fino ad arrivare, al termine del primo giro, giusto alla altezza dello scalino.
Leandro ripete pari pari il metodo usato da Umberto e da me stesso medesimo: conservazione della massa. Per forza torna lo stesso valore...
Diciamo, quindi, che l'approccio "fisico" è decisamente un approccio più che valido. Poi restano i due metodi: quello con lo scalino e la tangente e quello dell'appiccicata totale, ossia con vuoti trascurabili o nulli. Entrambi tendono a essere identici a quello fisico, dato che non vengono considerati spazi vuoti o, al limite, decisamente piccoli e trascurabili. Resta ancora l'approccio "teoricamente" più valido (almeno, a mio parere). Parlo di teoricamente, dato che il rotolo può essere schiacciato e le misure eseguite a priori saranno ben lungi dall'essere perfette. Per potere avere una conferma esatta, bisognerebbe svolgere la carta igienica e poi riavvolgerla (senza usarla). Ma, anche in questo caso, difficilmente si riuscirebbe ad avere lo stesso rotolo con le stesse dimensioni. Diciamo quindi che l'esercizio è chiaramente TEORICO, dato che bisognerebbe anche tenere in conto varie irregolarità che potrebbero creare spazi vuoti non prevedibili (senza arrivare fino all'isola che non c'è...).
Direi che ormai ciò che si deve ancora fare è abbastanza chiaro (fermo restando che si potrebbe seguire ancora una via di mezzo approssimata, ma praticamente identica... e più semplice).
Questa mattina ho fatto vedere il quiz ad Arley.
Quando è arrivato a leggere il paragrafo dei dati numerici, con le sue belle misure del rotolo e della carta, mi ha guardato in un modo strano, come fa quando trova un tartufo.
Allora gli ho chiesto: “perché fai quel muso, Arley? Cosa hai trovato?”
E 'sta bestia, invece di rispondermi, fa:
” Oreste, ma tu i dati dei problemi li prendi così, senza rifletterci sopra? Se uno ti spiega la formula di Erone e poi ti chiede di calcolare l'area di un triangolo con i lati 1cm 2cm 4 cm, parti subito a fare i conti ?”
“O bastalà, Arley, certo che no, si capisce subito che non è un triangolo, con quelle misure balorde”
“Allora, Oreste, spiegami come fa questo rotolo ad avere un numero intero di strati di carta di spessore uniforme, inalterabile, inossidabile, irrestringibile e costante di 0,36mm, tutti strati belli aderenti l'uno all'altro, che, nel loro insieme, sono spessi 55-20=35 cm. Non sarebbe logico che la misura di questo spessore fosse un multiplo intero di 0,36? Perché, se fosse un multiplo intero, facendo la divisione, 35/0,36 non verrebbe fuori un numero con i decimali. Che se vai a contarli, gli strati, i decimali mica li trovi.
Forse c'è uno strato più sottile?
Oppure, uno più spesso?
Oppure, non è vero che gli strati sono aderenti tra loro e la faccia inferiore di uno strato è staccata dalla faccia superiore dello strato precedente? E se ci fosse questo gap (ha proprio detto gap) non dovrebbe essere un dato del problema?”
Arley non è una bestia di quelle che abbaiano per niente, ci fa sempre prima il suo ragionamento.
Così ho cercato di prendere tempo e gli ho detto che mi sarei informato, che una spiegazione c'era di sicuro e gli avrei fatto sapere.
Aiutooo !
Potete sempre mettere 0.35... come volete voi... (i conti non cambiano) ma esiste anche uno strato non completato (e la misura del rotolo esterno ne deve tener conto, dato che il raggio è continuamente diverso e prima o poi passa anche per quel valore). Ovviamente se andate a scalini la cosa vi sembra impossibile, da cui si deduce che gli scalini non sono una bella scelta...
Mai vista la carta igienica con un cerchio più una bozza che ricorda uno scalino...
Guarda che "natura facit saltus" magari quantistico ... E la natura fa sempre ottime scelte.
E se guardi bene bene, lo scalino lo trovi , per quanto ammorbidito da strati e strati sovrapposti.
Se l'ultimo giro non è completo e si interrompe, avremo N strati da un lato e N+1 strati dall'altro, mai avremo un numero non intero di strati.
La variazione del raggio in modo continuo avviene solo perché al nastro si impone una traiettoria artificiale che lo lascia sospeso nel vuoto, distaccato dal suo supporto, introducendo uno spazio di intercapedine che varia lo spessore dello strato.
E comunque un modello matematico, su cui possiamo fare le considerazioni che vogliamo, anche se non è una buona scelta per rappresentare la realtà.
dipenderà anche da come viene costruita; se viene stirata o compressa. Se non sappiamo come viene costruita, come possiamo capire la sua realtà geometrica? Comunque per me l'unico calcolo serio è quello che voi chiamate conservazione della massa, mentre io eguaglianza fra i volumi. Lo usano nelle industrie per calcolare la lunghezza delle bobine . Non vedo inoltre applicazioni agli integrali; la lunghezza di una circonferenza è già un integrale. Qui per me il problema è discreto, a scatti di spessore s, tanti quanti sono la differenza fra i raggi.Quindi la somma di tante lunghezze di circonferenze. Ho fatto il conto con la spirale di Archimede, verrebbe 22.885, ma per me non c'entra niente. E' più piccolo, infatti il raggio varia linearmente, e non ha incrementi di s. Possiamo comunque solo risolvere il problema sotto le ipotesi di forma geometrica complessiva.
Se il raggio varia linearmente può raggiungere qualsiasi valore si voglia, indipendentemente dallo spessore. Inoltre, l'integrale porta a 22.907 anch'esso, anche se cambia poi nelle cifre decimali.
Va bene, lasciamo perdere la carta igienica e parliamo sempre di matematica pura o di pratica. Annulliamo pure la carta igienica e facciamo finta di averla usata tutta.
Al limite proporrò, in seguito, di calcolare la lunghezza di una spirale in coordinate polari.
FINIAMO QUI IL MIO STUPIDO TENTATIVO DI RENDERE DIVERSA DAL SOLITO UNA TEDIOSA SERIE DI FORMULE MATEMATICHE!
Prendiamo pure il risultato "fisico" della conservazione di MASSA e buona notte!!
Supponendo che la faccia inferiore del nastro si stacchi fin dall'inizio dal nucleo cilindrico e si distanzi progressivamente fino a raggiungere la quota S, il raggio varierà durante il primo giro, da R1 (iniziale) a R1+S (finale)
Al variare dell'angolo x , nullo nel punto di attacco, il raggio assume il valore seguente
R(x) = R1+ S (x/2π);
A fronte di una variazione dx la lunghezza di arco avvolta sarà R(x)dx.
Troviamo la lunghezza del primo giro:
numericamente : 20*2*3,1416 + 0,36*3,1416 = 125,664+1,131 =126,795 mm
La prima spira ha una lunghezza di 126,795/ 125,664 = 1,009 volte quella della circonferenza su cui si avvolge.
Anche le spire successive avranno questa forma e una lunghezza pari a 1,009 volte quella del cerchio di raggio fisso uguale al raggio iniziale della spira.
Occorre considerare che la faccia inferiore della spira 1 alla fine del suo giro ha raggio = 20,36 (questo è anche il raggio interno iniziale della spira 2 .
Dopo la prima spira intera il raggio interno è 20 + 1*0,36 e quello esterno 20 + 2*0,36
Dopo 96 spire intere il raggio interno vale 20 + 96*0,36 = 54,56 mm questo è il raggio iniziale della spira 97, il raggio esterno è 54,92 mm
Se si completasse questa spira 97, il raggio finale esterno sarebbe 55,28 superiore a 55, cosa non ammessa.
Dobbiamo quindi trovare la lunghezza esatta in corrispondenza alla quale il raggio esterno assume il valore = 55 mm
Sappiamo che la lunghezza di tutta la spira è 1,009 * 54,56*2*3,1416 = 345,8967 mm
Il tratto di spira che ci interessa ha lunghezza pari a 345,8967 * (55-54.92)/0,36 = 76,8659 mm
La spira intera 96 (pari) ha lunghezza 1,009 * 54,2 *2*3,1416 = 343,6144 mm
Ora abbiamo le lunghezze della spira 96 e della frazione di spira 97 che ci consente di arrivare al raggio massimo.
Le possiamo sommare e otteniamo 420,4803 mm.
Resta da valutare la lunghezza dell 95 spire più interne. Il numero di esse è dispari e la spira intermedia (95+1)/2 è la spira numero 48.
Il suo raggio iniziale vale 20 + 48 *0,36 = 37,28 mm la sua lunghezza è 1,009*37,28*2*3,1416
= 236,3458 mm
La lunghezza complessiva delle prime 95 spire è 95*236,3458 = 22452,8543 mm
a questo valore resta solo da sommare la lunghezza (spira 96 e parte di 97) = 420,4803 mm per avere la lunghezza totale = 22873,3346 mm
Questo risultato è inferiore di 34,2 mm rispetto al valore 22.907,5 ottenuto su altri modelli. si tratta di uno scarto percentuale di circa 1,5 per mille.
Un risultato ancora diverso e più preciso si può ottenere mediante il calcolo della lunghezza della curva.
Operando sulla equazione polare, (raggio in funzione dell'angolo ) si dovrà calcolare un integrale di questa forma:^2+f(\theta&space;)^2}d\theta)
dove a e b sono i valori iniziale e finale dell'angolo 
, ossia zero per a e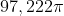 
= 610,867 per b,
Conto sulle vostre correzioni in caso di errori.
il mio calcolo partiva dalla considerazione che l'infinitesima lunghezza è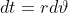
e il valore è
22907,4464324256
esattamemnte quello del Professore, purtroppo i database del sito si è mangiato i miei calcoli
abbi pazienza Leandro... speriamo che tutto torni a funzionare presto! E tra noi il professore si può eliminare: Enzo e basta!!