Questo è il secondo articolo della serie "Ponti sospesi, catenarie, parabole & co."

 

Iniziamo il nostro lungo percorso verso i ponti sospesi partendo da lontano. In particolare, dalle funzioni trigonometriche che conosciamo tutti molto bene. E' indiscutibile che esse siano funzioni che lavorano sopra degli angoli. In altra parole, considerato un certo angolo, una funzione trigonometrica lo trasforma in un certo numero. Mettiamole nuovamente in evidenza in Fig. 1, considerando una circonferenza di raggio unitario, la cui espressione analitica è:

x² + y² = 1                          .... (1)

Per semplicità, utilizziamo solo l'arco  compreso tra l'asse delle x e quello delle y, entrambi nella zona positiva (primo quadrante).

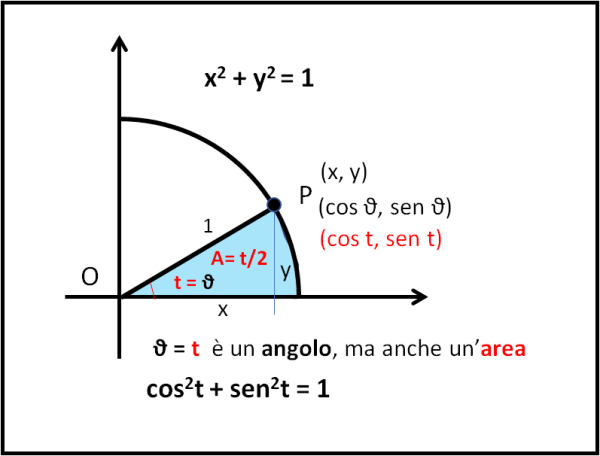
Ogni punto della circonferenza può essere individuato da una x e da una y, tali che soddisfino la  (1).

Tuttavia, la posizione di ogni punto può anche essere espressa in coordinate polari, ossia attraverso l'angolo θ e il raggio  che congiunge l'origine degli assi con il punto. Nel caso che stiamo trattando, il raggio è unitario e quindi ogni punto è individuato dall'angolo θ.

Quale legame vi è tra le coordinate cartesiane x e y e le coordinate polari? Il legame viene espresso proprio attraverso le funzioni trigonometriche seno e coseno, attraverso le relazioni ben conosciute:

x = 1 cos θ = cos θ

y = 1 sen θ = sen θ

In altre parole il punto P può essere individuato sia dalla coppia (xP, yP) sia dalla coppia di funzioni trigonometriche (cos θ, sen θ).

Da questo legame si ottiene immediatamente una delle formule più usate in trigonometria. Basta considerare l'equazione (1) e inserire al posto di x e y, i corrispondenti valori delle funzioni trigonometriche:

x² + y²= 1

cos²θ + sen²θ = 1

Formula che rappresenta praticamente l'equazione di una circonferenza di raggio unitario espressa in coordinate polari.

Potremmo anche accontentarci e lo abbiamo fatto fino ad ora... Ma, invece, cerchiamo di definire le nostre funzioni trigonometriche in un modo diverso, facendo comparire non più un angolo ma un'area!

La cosa non è certo difficile...

Chiamiamo A  l'area del settore circolare riempito di azzurro nella figura. Quanto vale A ?

Basta utilizzare una semplice proporzione... L'area di tutto il cerchio sta all'area del settore t come l'angolo al centro, corrispondente a tutto il cerchio, sta all'angolo corrispondente al settore circolare.

Area cerchio = π 1² = π             (il raggio è unitario)

Angolo al centro dell'intero cerchio = 2π   (espresso in radianti)

Angolo al centro del settore circolare = t   (il nostro θ espresso in radianti)

Da cui:

π : A = 2π : t

A = π t /2π = t/2

t = 2 A

In altre parole, l'angolo t (in radianti) non è altro che il doppio dell'area del settore.

La scrittura

cos t ( sen t)

si può quindi leggere come:

il coseno (il seno) di un certo angolo non è altro che il coseno (il seno) del doppio dell'area del settore circolare di angolo al centro t.

Qualcuno mi chiederà: "Ma c'era proprio bisogno di scrivere un'area al posto di un angolo? La trigonometria era già "antipatica" nel modo "normale". A parte che la trigonometria NON è antipatica, ma utilissima e spesso divertente, la ragione di questa "trasformazione" è che vogliamo passare da una circonferenza di raggio unitario a un'altra conica: l'iperbole equilatera unitaria, ossia:

x² - y² = 1                                .... (2)

Anche per questa curva (considerata nel primo quadrante) possiamo tranquillamente dire che ogni suo punto è definito da una coppia di valori delle  coordinate x e y. Tuttavia, possiamo anche utilizzare delle funzioni trigonometriche un po' speciali, in modo del tutto analogo a quanto appena dimostrato per le funzioni trigonometriche "normali".

x = cosh t

y = sinh t

dove t ha lo stesso significato di poco fa, ossia è uguale al doppio dell'area  colorata in rosso in Fig.  2.

Come si può notare, queste nuove funzioni non sono legate a un angolo, ma a un'area. Tuttavia, possono essere chiamate anch'esse come seno e coseno dato che anche questi ultimi possono essere legati tranquillamente a un'area. L'unica differenza è il tipo di area che consideriamo: nel caso "normale" l'area di una settore circolare (in realtà, il doppio di quest'area); nel "nuovo caso" l'area compresa tra l'iperbole equilatera, l'asse delle x e la congiungente il punto P con l'origine (in realtà, il doppio di quest'area).

Queste nuove funzioni, essendo basate su un'iperbole e non su un cerchio, vengono chiamate funzioni (trigonometriche) iperboliche e il seno e il coseno vedono l'aggiunta di una h (da hyperbola) nel loro simbolo.

Anche loro, inserite nella (2) portano a un'espressione di grande importanza: