Finalmente una matematica accessibile a tutti: basta seguire il tag Ramsey  dove sono illustrati i prerequisiti per capire uno dei teoremi più strani che io abbia mai visto, dall'enunciato semplice, che potrebbe comprendere anche un bambino. Chi vuole può seguire anche la dimostrazione che è un pò più complessa, ma anche qui  non sono previste nozioni di matematica avanzata. Vedremo poi nel seguito a quali problemi possano essere applicati questi argomenti.

Due parole su chi era Ramsey, tratte direttamente da Wikipedia:

"Frank Plumpton Ramsey (Cambridge, 22 febbraio 1903 – Londra, 19 gennaio 1930) è stato un matematico, logico, statistico ed economista inglese. Diede importanti contributi nel campo della filosofia, logica matematica, probabilità ed economia."

Per la prima volta forse, parlo prima del personaggio che delle sue teorie; quest' uomo, vissuto solo 26 anni mi impressiona perchè ricorda Galois, vissuto solo 21, ma entrambi hanno lasciato un segno indelebile nel mondo della matematica. Ramsey aveva una mente senz'altro privilegiata; non facciamo paragoni alla storiella delle somme scoperte da Gauss per evitare le punizioni del maestro,  ma pensate che da adolescente conobbe un certo  filosofo Ogden che  gli diede un dizionario e una grammatica tedesca oltre ad un complicato testo di filosofia, dicendogli "Usa la grammatica e il dizionario e dimmi cosa ne pensi del testo". Circa una settimana dopo aveva non solo imparato il tedesco, ma aveva pure delle obiezioni alle teorie presentate nel testo.

Detto questo, la fantasia e l'intelligenza di Ramsey lo  spinsero ad affrontare dei problemi senz'altro originali di matematica discreta, quali i problemi di colorazione di un grafo completo. Abbiamo visto in questo articolo  una breve spiegazione di cos'è un grafo e che cos'è un grafo completo; riporto qui una breve parte dell'articolo:

Un grafo, è proprio quello che ci propone intuitivamente la parola "grafo"; un grafo serve per tradurre in ambiente grafico determinati problemi matematici.

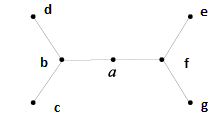
Una rappresentazione di questo tipo prende  il nome di grafo. .

I punti  a,b,c,d,e,f,g si chiamano vertici o nodi; gli archi che li uniscono sono gli spigoli o lati del grafo. Il grado di un nodo è invece il numero di lati che convergono in un nodo. Notiamo una cosa importante; possiamo percorrere il lato di un nodo in entrambi le direzioni, ossia sia entrando nel nodo che uscendone. Una cosa molto importante in un grafo è la connessione: un grafo è connesso se comunque siano scelti due nodi, esiste un percorso che li unisca. Ci occuperemo principalmente di grafi connessi.

Diremo che un grafo è completo se  ogni vertice è collegato a tutti i vertici rimanenti.

Nella figura seguente potete vedere vari  esempi di grafi completi.

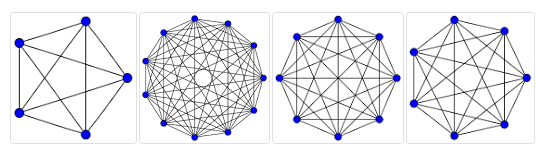
Ramsey si occupò di problemi inerenti alla colorazione dei grafi completi. Attenzione: parliamo di colorazione perchè è la proprietà più semplice e visivamente efficacie. In realtà queste teorie sono applicabili anche in questo senso: qual è il minor numero di elementi necessario affinché una certa proprietà sia vera?

Tanto per formalizzare un po' le cose, chiamiamo  un grafo completo con n vertici. Chiamiamo adesso colorazione di un grafo una qualsiasi assegnazione di colori, presi da un certo insieme, ai lati dei grafo che chiamiamo G. Dato un grafo G a cui sia stata assegnata una tale colorazione, diremo che un sottografo di G è  monocromatico se, nella colorazione data, i suoi lati hanno tutti lo stesso colore (cosa sia un sottografo di G è abbastanza intuitivo; basta prendere il grafo completo composto da un sottoinsieme di vertici di G).Il problema che ci proponiamo adesso è il seguente: in  esiste sempre, qualsiasi sia la colorazione, un triangolo monocromatico, ovvero un sottografo con tre vertici? La risposta è no basta guardare la figura seguente:

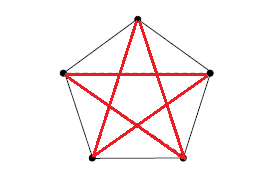
Ci basta infatti solo un controesempio: questa colorazione rosso-nera non contiene nessun triangolo monocromatico. Vi faccio notare che la colorazione è la cosa più semplice che possiamo usare nel caso dei grafi; ma nei problemi reali può essere una qualsiasi altra relazione fra coppie di  oggetti. E in  ? Questo lo abbiamo visto in un quiz:

Chiamiamo   un grafo completo con 6 vertici, ovvero un grafo in cui ogni vertice è collegato con tutti gli altri. E' vero o falso che, comunque colorando i lati del grafo con due colori, esiste sempre un triangolo monocromatico contenuto in esso?

In K6 si,è possibile, qualsiasi sia la colorazione.

Da qui per passare ai teoremi di Ramsey, il passo è breve; Nella sua forma più semplice, il Teorema di Ramsey è la generalizzazione all'esistenza, in grafi completi con un numero sufficientemente grande di vertici, di un sottografo monocromo con n vertici, .

Ramsey dimostrò che il disordine completo non può esistere. Qualunque insieme di enti sufficientemente grande contiene necessariamente una configurazione molto regolare.

Ma veniamo alle definizioni e all'enunciato del teorema:

Teorema 1) (Ramsey 1930) Per ogni n >= 1, esiste un intero R(n) tale che, data una qualsiasi colorazione dei lati del grafo completo mediante due colori, esiste un sottografo completo Kn monocromatico.

Chiaramente, con questa definizione si capisce poco o niente, e può confondere. Chiariamo il tutto con gli esempi fatti sopra;

se n=3, siamo nel caso del triangolo, quindi cerchiamo  R(3); R(3) non è 5 , ovvero  K5 che non può contenere un triangolo monocromatico, come visto sopra. Mentre invece R(3) è proprio uguale a 6;  Infatti K6 contiene un triangolo (sottografo) monocromatico qualsiasi sia la colorazione, come visto nel quiz.

Ma veniamo ad un caso più generale del teorema, che stranamente si dimostra in modo più semplice;

Teorema 2) Dati n,m >= 2, denotiamo con R(n,m) il più piccolo intero  tale che data una qualsiasi colorazione dei lati del grafo completo KR(n,m) mediante due colori b e c, esiste un sottografo b-monocromatico  Kn oppure un sottografo c-monocromatico  Km.

Di conseguenza Il numero R(n) del primo teorema  coincide quindi con R(n, n); inoltre, chiaramente, R(n,m) = R(m, n).

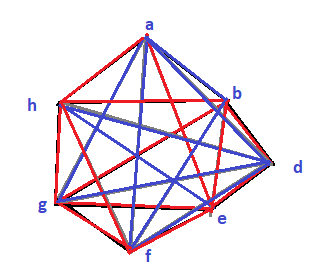
Per trovare R(4,3) ci serve trovare il grafo che contenga almeno uno dei due sottografi completi con 3 o quattro vertici, che abbia il numero minimo di vertici. Questo è in parole povere ciò che richiede il Teorema. Notiamo che R(4,3)= R(3,4).  E inoltre , se n=m=3 per esempio, se troviamo R(3,3) allora troviamo anche R(3)

Quindi ,   riassumendo (e ripetendo), Il numero R(n) del teorema precedentemente enunciato coincide quindi con R(n, n); inoltre, chiaramente, R(n,m) = R(m, n)

Se adesso riusciamo a dare risposta al secondo teorema, dimostreremo anche il primo.

(chiameremo blu il colore b e rosso il colore c)

Per risolvere il teorema, ci serviamo di questi due punti, 1,2 (che di solito si chiamano lemmi)

Per ogni n;m , R(n;m) esiste e valgono le seguenti relazioni:

1) R(n, 1) = n per ogni n .

2) R(n;m) <=R(n - 1;m) + R(n;m - 1).

Dimostriamo il teorema per induzione su m+n

(il principio di induzione vale su qualsiasi variabile naturale z; se poniamo z=n+m facciamo scorrere tutti i valori a z variando in tutti i modi possibili m,n; chiaramente se n=m abbiamo lo stesso valore di z, ma anche che R(n,m)=R(n,n)=R(m,m); inoltre z= n-1 +m =n+m-1,  e n+m è il precedente di z, n+m)

È evidente dalla definizione di R(n,m)che per tutti gli n , R ( n , 1) = R (1, n ) = 1.Il minimo sottografo completo è un lato, che è  banalmente monocromatico. Questo avvia l'induzione. Dimostriamo che R ( n , m ) esiste trovando un limite superiore per esso (nel senso che non è infinito, come ci si potrebbe aspettare). Per ipotesi induttiva R ( n  - 1,m ) e R (n ,m  - 1) esistono. Esistono dunque due grafi con R ( n  - 1,m ) , R (n ,m  - 1) vertici che soddisfano alle condizioni del teorema 2)

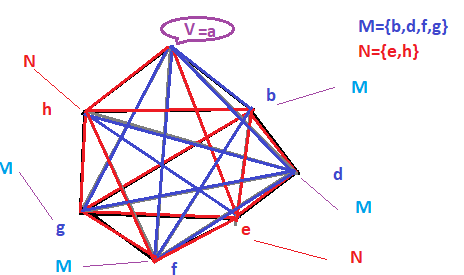
Si consideri un grafo  con r= R ( n  - 1, m) + R ( n , m  - 1) vertici i cui lati sono colorati con due colori.  Vogliamo dimostrare  che Kr contiene come sottografo o un Kn blu oppure un Km rosso.Scegliamo un vertice v dal grafo, e isoliamo i rimanenti vertici in due insiemi M e N , tale che per ogni vertice w , w è in M se il lato ( v , w ) è blu, e w è in N se il lato ( v , w ) è rosso. Poiché il grafo ha r= R ( n - 1, m) + R ( n , m- 1) = | M | + | N | + 1 vertici, ne consegue che :

o | M | ≥ R ( n - 1, m ) o | N | ≥ R ( n ,m - 1). Nel primo caso, se M ha un  Km di colore rosso  così fa il grafo totale (di r vertici) e abbiamo finito.

Altrimenti M ha un  K n -1 blu e così M ∪ { v } ha un Kn blu per definizione di M .

L'altro caso, | N | ≥ R ( n ,m - 1), si risolve in modo  analogo.

I numeri R(n;m) sono detti numeri di Ramsey e sono noti solo in pochi casi: R(3, 3) = 6, R(3,4) = 9, R(3, 5) = 14, R(3, 6) = 18, R(3, 7) = 23, R(3,8) = 28, R(3, 9) = 36, R(4, 4) = 18 e R(4, 5) = 25.

Nel prossimo articolo su Ramsey vedremo delle importanti applicazioni  del teorema.