Questo è il quarto articolo della serie "Ponti sospesi, catenarie, parabole & co."

Verifichiamo ancora una volta il significato delle funzioni iperboliche e vediamo che forma hanno. In fondo, è proprio questa  forma che ci verrà utile in seguito, anche per comprendere le argomentazioni di Galileo Galilei.

Questo articolo è forse perfino sovrabbondante. In effetti, abbiamo già definito le funzioni iperboliche attraverso una rappresentazione geometrica in cui l'argomento delle funzioni iperboliche è un'area e non un angolo, Abbiamo anche mostrato che le funzioni trigonometriche classiche possono essere definite anch'esse considerando come argomento non un angolo, ma un'area. D'altra parte siamo anche riusciti a scrivere l'equazione dell'iperbole in forma parametrica, ossia utilizzando un parametro t che compare in relazioni di tipo esponenziale. Per essere precisi fino in fondo non ci resta che dimostrare che il parametro t delle equazioni parametriche è proprio il doppio dell'area che abbiamo definito per la definizione delle funzioni iperboliche, nel primo capitolo.

Le equazioni parametriche sono:

x = (e^t + e^-t)/2   

y =  (e^t - e^-t)/2   

che, abbiamo visto, soddisfano perfettamente l'equazione dell'iperbole in forma canonica

x² - y² = 1

Vogliamo dimostrare che il parametro t è proprio il doppio dell'area che ci è servita per definire geometricamente le funzioni iperboliche.

Torniamo perciò alla nostra figura del Capitolo 1 e vediamo di calcolare un po' di aree (Fig. 3)...

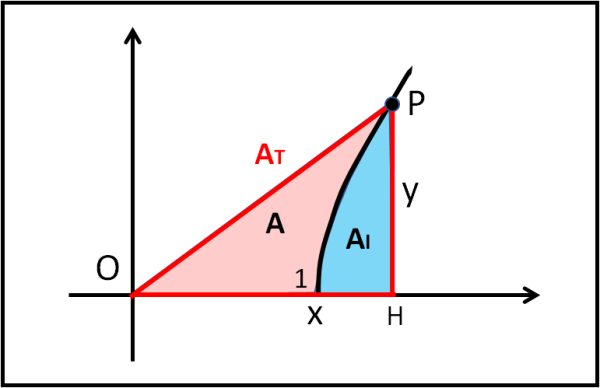
Un punto qualsiasi P dell'iperbole ha come coordinate x e y. Ne segue che il triangolo OHP ha un 'area A_T data da:

A_T = xy/2

Per determinare l'area A che ci interessa dobbiamo togliere a quest'area quella, A_I, compresa tra l'iperbole e l'asse delle x. Per calcolare quest'area dobbiamo fare uso di un integrale  definito, ricordando che l'integrale definito non fa altro che sommare tanti piccolissimi rettangoli di base dx e altezza y, con dx tendente a zero.  Nel nostro caso i limiti d'integrazione sono x = 1 e  x = x_P.

A_I = ∫₁^x_P y dx  

L'area che ci interessa vale perciò:

A =  A_T - A_I = xy/2 - ∫₁^x_P y dx  

Molto bello, ma noi dobbiamo fare entrare in gioco il parametro t. Nessun problema per la prima parte:

A_T = xy/2 = ((e^t + e^-t)/2  · (e^t - e^-t)/2 )/2 =  (e^t + e^-t)(e^t - e^-t)/8

Applicando il solito prodotto notevole (a  + b)(a - b) = a² - b²

A_T = (e^2t - e^-2t)/8

Meno banale  la seconda parte...

Tuttavia, basta ricordare che

dx/dt = d((e^t + e^-t)/2)/dt 

dx/dt = (e^t - e^-t)/2

Abbiamo solo derivato la funzione (e^t + e^-t) ricordando che la derivata della somma è la somma delle derivate  e che la derivata di e^-t vale -1 · e^-t = - e^-t.

Ne segue che possiamo ricavare dx in funzione di dt

dx = dt (e^t - e^-t)/2

Passiamo ai limiti di integrazione. Quando x = 1 è ovvio che t =0. Quando x vale x_P, la t è quella corrispondente a un certo t di P. Ma la t_P è a sua volta variabile con il punto P e quindi è in realtà la t che compare nell'equazione. Anche se dovremmo introdurre una nuova variabile qualsiasi (ad esempio u) per non avere all'interno dell'integrale lo stesso t del limite d'integrazione, noi ce lo permettiamo ugualmente per non confondere le idee. Ricordiamo solo che t dentro l'integrale è la variabile, ma è anche un limite di integrazione (a sua volta variabile al variare del punto P).

A_I = ∫₁^x_P y dx = ∫₀^t ((e^t - e^-t)/2 )((e^t - e^-t)/2 ) dt

A_I = (1/4)∫₀^t  (e^t - e^-t)² dt = (1/4)∫₀^t  (e^2t - 2 e^t e^-t + e^-2t) dt = (1/4)∫₀^t  (e^2t - 2+ e^-2t) dt

Ricordiamo che l'integrale di una somma è uguale alla somma degli integrali, per cui è facile calcolare l'integrale:

∫₀^t  (e^2t - 2+ e^-2t) dt = ∫₀^t  e^2t  dt  - 2∫₀^t  dt  + ∫₀^t  e^-2t dt = [e^2t/2]₀^t - 2[t]₀^t  - [e^-2t/2]₀^t 

 ∫₀^t  (e^2t - 2+ e^-2t) dt  = e^2t/2 - 1/2 - 2t - e^-2t/2 + 1/2 = e^2t/2  - 2t - e^-2t/2 

Unendo insieme, abbiamo:

A = (e^2t - e^-2t)/8 - (1/4)(e^2t/2  - 2t - e^-2t/2) = e^2t /8 - e^-2t/8 - e^2t/8 + t/2 + e^-2t/8

A = t/2

Come volevasi dimostrare: l'area a cui ci si riferisce quando si parla di argomento delle funzioni iperboliche è proprio la metà di t !

Disegniamo le curve

Diventa praticamente un gioco da ragazzi disegnare le funzioni senh x e cosh x nel piano cartesiano.

Attenzione: disegniamo le funzioni, non l'iperbole, così come disegniamo le funzioni sen x e cos x e non il cerchio di raggio unitario.

Basta riferirsi alla loro forma  parametrica e ... dividerla in due parti

y= senh x = (e^x - e^-x)/2   = e^x/2 - e^-x/2

y= cosh x = (e^x + e^-x)/2   = e^x/2 + e^-x/2

Nel primo caso dobbiamo fare la differenza tra due funzioni elementari  y1 = e^x/2 e y2 = e^-x/2, rappresentate in Fig. 4 con le linee rosse (lascio a voi il piacere di confermare l'andamento facendo qualche limite...).

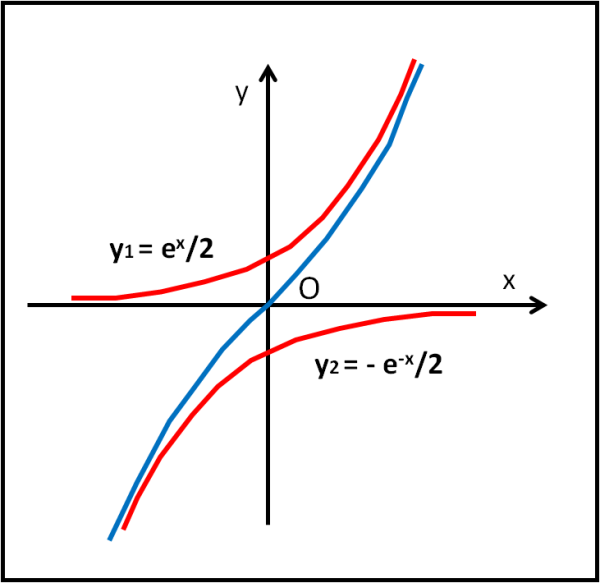
La linea azzurra è ovviamente il senh x. La funzione passa per l'origine in quanto per x = 0 la y1 vale 1/2 mentre la y2 vale - 1/2.

In Fig. 5 viene invece rappresentato, in azzurro, il cosh x, che per x = 0 vale 1 (1/2 + 1/2).

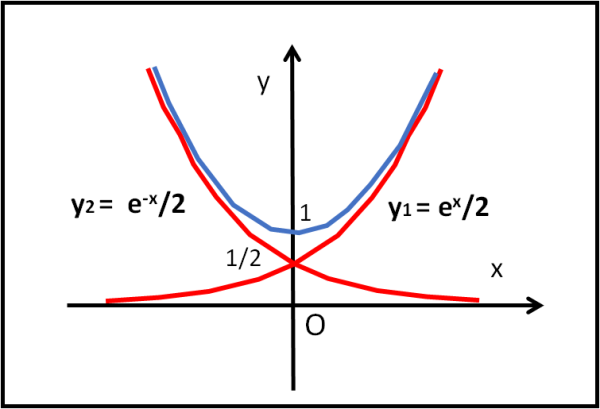
L'ultima curva assomiglia tanto a una parabola e si può già capire come anche un genio come Galileo Galilei possa essere -forse- caduto in errore.

Possiamo concludere che, come nel caso della trigonometria classica, anche in quella iperbolica valgono formule del tutto analoghe, oltre che ad esistere  funzioni come la tangente iperbolica e via dicendo.

E' anche facilissimo calcolarne le derivate e noi lo facciamo per il senh e il cosh, dato che ci verranno utili in seguito:

d(sinh(x))/dx = d((e^t - e^-t)/2 /dx = 1/2 (e^t -(- e^-t)) = ( e^t + e^-t)/2 = cosh(x)

d(cosh(x))/dx = d((e^t + e^-t)/2 /dx = 1/2 (e^t - e^-t)) = sinh(x)

Esistono anche le funzioni inverse e può essere interessante lasciare la loro  rappresentazione come esercizio per chi ha voglia di cimentarsi...