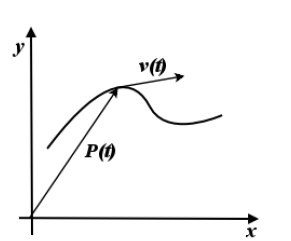
Purtroppo ancora un articolo tecnico; del resto per affrontare a grandi linee la dimostrazione della congettura, abbiamo bisogno di alcuni concetti di geometria differenziale. In questo articolo cominciamo ad affrontare la curvatura di una linea. E' l'esempio più facile di curvatura di una varietà; il caso n=1. La curvatura di una linea, ci servirà poi per analizzare la curvatura di una superficie, per poi astrarci al caso più generico di varietà di dimensione qualsiasi (il tensore di curvatura d Riemann).