Mi sono posto il problema se la soluzione ottimale del quiz (molto interessante) posto da Vincenzo sia  effettivamente 14. Questo è molto difficile da dimostrare analiticamente, forse addirittura impossibile (non lo so). Ma quando si parla di ottimizzazioni, è sempre meglio cercare degli algoritmi che risolvano per noi il problema. In parole povere, affidarlo ad un calcolatore. Ma non è che il computer risolve per noi il problema solamente perchè glielo chiediamo; si tratta di costruire  un algoritmo che analizzi tutti i casi (soluzioni) possibili e le compari, per trovare quella minima. Una volta scritto l'algoritmo, ovvero creato un sistema di calcolo atto allo scopo, potemmo anche applicarlo noi direttamente. Fatto sta che ci metteremmo una vita ad eseguirlo. Il Computer è stupido, e fa solo quello che diciamo noi; ma lo fa in modo velocissimo e senza compiere errori. Il nostro ruolo ,peraltro indispensabile, sta nel tradurre il problema in un linguaggio matematico, da poi proporre al computer con un ulteriore linguaggio di programmazione. L'esposizione che farò del problema è completamente generalizzata; non si parlerà di due uova e 100 piani, ma di di n uova e k piani. Perchè? Perchè lo stesso problema si potrà ridurre in sottoproblemi con un numero minore di uova o  (soprattutto) di piani . Mi spiego meglio; se parto da n piani e k uova, le uova diminuiscono ogni qualvolta si verifica una rottura, mentre i piani da esplorare diminuiscono ogni qualvolta l'uovo non si rompe. L'idea, fra l'altro semplicissima ma impossibile da  realizzare " a mano" è la seguente; quando lasciamo cadere un uovo da un piano X, ci possono essere due casi

i) L'uovo si rompe

ii) L'uovo non si rompe.

1) Se l'uovo si rompe dopo essere caduto dal piano X, dobbiamo solo verificare la presenza di piani inferiori a x con le uova rimanenti; quindi il problema si riduce a x-1 piani e n-1 uova
2) Se l'uovo non si rompe dopo essere caduto dal piano X, dobbiamo solo verificare la presenza di piani superiori a x; quindi il problema si riduce a k-x piani e n uova.

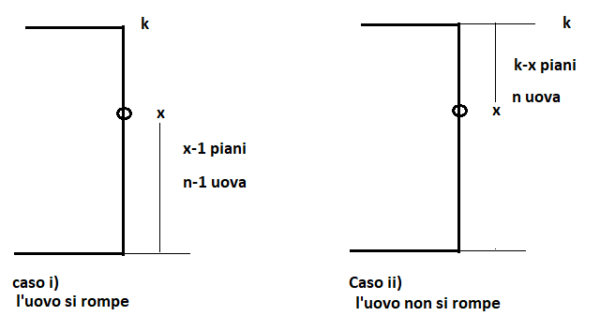
Dato che dobbiamo ridurre al minimo il numero di prove nel caso peggiore , prendiamo il massimo dei due casi. Consideriamo il massimo dei due casi sopra per ogni piano e scegliamo il piano che produce il numero minimo di prove.

k = Numero di piani n = Numero di uova

lanci (n, k) = Numero minimo di prove necessarie per trovare il piano critico nel peggiore dei casi.
Traduciamo l'algoritmo in modo ricorsivo:
*) lanci (n, k) = 1 + min {max (lanci (n - 1, x - 1), lanci (n, k - x)): x che varia in {1, 2, ..., k}}
notare che la funzione  che eseguiamo in *) si rifà alla stessa ricerca in un caso più piccolo; prima poi
arriveremo ai casi di soluzione immediata, che vedremo in dettaglio più avanti.

Una volta i programmatori usavano i diagrammi di flusso; altro non erano che una successione di  simboli e frecce che indicava la sequenza delle operazioni. Nel caso delle funzioni ricorsive, questo non è molto indicato, forse addirittura impossibile.  Bisogna cercare di pensare in astratto a cosa succede a seconda delle condizioni che si verificano. I programmatori sono abituati ad usarle, ma molto spesso riescono a confondersi anche loro. L'esempio più efficacie di funzione ricorsiva consiste nel calcolo del fattoriale di n:

n!=n*(n-1)!

La funzione rappresentata da ! viene richiamata da se stessa; per calcolare n! mi riduco a calcolare (n-1))! e a moltiplicarlo per n, e decremento n fino ad arrivare ad 1. In questo caso , sapendo che 1!=1 alla fine ho trovato il risultato cercato. Nel nostro caso afferrare il concetto è un po' più difficile, perchè comporta la doppia applicazione della funzione stessa, ma il concetto rimane lo stesso: vogliano arrivare ai casi semplicissimi:K=1 o k=0 che danno come risultato k, o n=1 (un uovo) che dà come risultato k (piani) di lanci.

Ma torniamo al nostro problema; la soluzione esposta " a parole" si traduce in linguaggio** software nel seguente listato (io uso il linguaggio Vbnet, di Visual studio), che riporto per conoscenza, ma di cui non è necessario comprenderne i particolari. Chi preferisce, può saltare direttamente al testo successivo.

(** ciò dimostrerà,  al di là di ogni dubbio, che applicando il software al nostro caso (2,100) , il minimo numero di lanci è proprio 14)

Public Function max(ByVal a, ByVal b) As Integer

If a <= b Then
Return b
Else
Return a
End If
End Function

(questa funzione serve solo per cercare il massimo fra due valori, non essendo contemplata nel Vbnet)

Questa è invece la funzione vera e propria che traduce per il calcolatore quanto detto nelle frasi 1),e 2)

Public Function lanci(ByVal n, ByVal k) As Integer
'n numero uova
' k numero piani
Dim ris As Integer

If k = 1 Or k = 0 Then
Return k
End If
If n = 1 Then
Return k
End If
Dim min As Integer
min = Integer.MaxValue

Dim x As Integer
For x = 1 To k

ris = max(lanci(n - 1, x - 1), lanci(n, k - x))

If ris < min Then
min = ris
End If

Next

Return min + 1

End Function

Per risolvere il nostro problema, basta quindi applicare la funzione ai valori (2,100):

RIS=lanci(2,100), e visualizzarla a video in qualche modo.

In verità, tale funzione è comprensibile  a chi abbia studiato un minimo di programmazione; l'istruzione condizionale if A ..Then B che traduce in linguaggio di programmazione " se vale A esegui B.." penso sia nota. L''istruzione for x=1 to k.. next esegue un ciclo e finisce quando x raggiunge il valore k.  Questo codice di programmazione funziona, ma purtroppo ha una complessità molto alta. Cos'è la complessità di una procedura, di un algoritmo? E' il numero dei tentativi massimi che dobbiamo fare per raggiungere il nostro risultato. Nel nostro caso , tale ordine dipende da k in modo esponenziale, cioè vale circa 2^k; capirete che nel nostro caso 2^100 è un numero pressochè irraggiungibile. Non basta fare il più semplice  programma del mondo per risolvere il problema (ricordate il paradosso di Borel?) ma bisogna farlo in modo di risolverlo in tempi reali.

Riporto per tale motivo alla fine dell'articolo una versione più evoluta della procedura, per chi vuole approfondire. Essa si basa su moderne tecniche di programmazione dinamica su Array (matrici) dinamici, e permette nel nostro caso di ridurre l'ordine di  complessità a nk^2.

Ho tradotto il codice in un software che permette di inserire vari valori sia per n che per k; potete scaricarlo da qui , scompattare il file e lanciare l'eseguibile lanci.exe, che vi farà apparire la seguente finestra:

di default nelle caselle di testo ho messo i dati del problema, ma potete divertirvi anche con altri valori.

 

Procedura che sfrutta la dinamicità degli array (per chi vuole leggerla):

Public Function lanci_uova(ByVal n, ByVal k) As Integer

Dim piani As Integer(1000,1000)
Dim i, j, x, res As Integer

For i = 1 To n
Dim a As Integer
a = 1
'Dim matrice As Integer(,) = New Integer(1, 3) {{1, 2, 4, 5}, {2, 4, 5, 6}}
piani(i, 1) = a

piani(i, 0) = 0
Next

For j = 1 To k
piani(1, j) = j

Next

For i = 2 To n

For j = 2 To k
piani(i, j) = Integer.MaxValue
For x = 1 To j
res = 1 + Me.max(piani(i - 1, x - 1), piani(i, j - x))

If res < piani(i, j) Then
piani(i, j) = res
End If
Next
Next

Next

Return piani(n, k)

End Function