Nella vorticosa fucina del blog, ogni tanto succede che si producano contemporaneamente articoli gemelli, del resto anche nel mondo dei numeri esistono i “primi gemelli” e tutti ne hanno profondo rispetto. L'ultimo di questi casi riguarda la metamorfosi della catenaria in parabola, evento che è sotto i nostri occhi ogni volta che osserviamo un ponte sospeso.

Questo è il settimo articolo della serie "Ponti sospesi, catenarie, parabole & co."

Vincenzo e Maurizio vi propongono le loro riflessioni incrociate (alias "parabole", nel senso di racconti brevi il cui scopo è spiegare un concetto difficile con uno più semplice) sul tema in questo articolo.

Catenaria o Parabola? Tertium datur.

Da una torre all'altra si distendono pigramente i mastodontici cavi, scendono dalla altezza di 225 metri, incurvandosi flessuosamente per più di seicento metri, fino al punto più basso e risalgono con identica curva alla medesima altezza, sulla torre opposta. La curva è quella stessa che formano i cavi dell'alta tensione che vanno da un traliccio all'altro di una linea elettrica o, più modestamente, quella che si forma ogni volta che tiriamo una corda tra due sostegni per appendere la biancheria ad asciugare. Il suo nome è catenaria, anche se assomiglia ad un'altra curva più familiare: la parabola.

Ma quando quei cavi verranno concretamente collegati alle strutture del ponte, cosa succederà alla catenaria? In che modo e misura il carico che dovranno sostenere potrà deformare il loro assetto?

L’impalcato del ponte, ossia la strada su cui scorre il traffico veicolare, ha un suo peso, a cui va aggiunto il peso della “travata”, ossia quella struttura reticolare di travi che regge l’impalcato, a cui va aggiunto anche il peso dei veicoli transitanti, a cui andrebbe aggiunta ancora la forza di spinta dei venti, di cui peraltro parleremo in altra sede. Solo se tutto ciò non avesse alcun peso, non esercitasse alcuna sollecitazione, la curva disegnata dai cavi resterebbe quella che si presenta a vuoto: una catenaria. Pur tralasciando l’effetto del vento, e supponendo di vietare il traffico sul ponte, resta il fatto che le sue strutture, agganciate ai cavi mediante i tiranti verticali, o pendini, hanno un loro peso, e questo peso è nettamente preponderante su quello dei cavi.

Il Golden Gate Bridge: un esempio emblematico di ponte sospeso, ha un peso di 887.000 tonnellate, i due cavi a cui è aggrappato pesano 45.000 tonnellate, non certo poco, ma meno del 5% del totale.

Questa diversa distribuzione del peso avrà conseguenze inevitabili sulla silhouette della curva disegnata dai cavi, non potrà più essere la elegante catenaria, modellata dalla distribuzione uniforme del peso lungo il cavo, ma sarà una curva più acuta della quale potremmo calcolare l’equazione mediante formule matematiche, ma che preferiamo, per ora, farvi intuire con un semplice ragionamento.

Non è certo una grande scoperta il fatto che se appendete un peso concentrato al centro di una corda per stendere la biancheria, quanto maggiore è il peso, tanto più pronunciata sarà la inclinazione dei tratti di corda ai suoi lati. Come non è inatteso il fatto che se vi sedete su una panca il cui sedile è costituito da una leggera asse disposta (apparentemente) su un piano orizzontale, il vostro peso lo deformerà flettendolo e, finché resterete seduti, non sarà più il piano che era prima del vostro arrivo. Perché mai stupirsi del fatto che la catenaria è destinata a modificarsi?

Allontanandoci appena un poco dalla percezione intuitiva che deriva dalla nostra esperienza quotidiana nel mondo reale, riflettiamo su questi dati di fatto:

Un punto P della catenaria è soggetto alla forza peso e alla reazione vincolare degli estremi.

Quando, mediante i tiranti verticali, il ponte viene collegato al cavo, questo punto P è soggetto alla forza peso, alla reazione vincolare, e in più sorregge la massa di un tratto di ponte sottostante, un tratto lungo come l’intervallo tra due tiranti adiacenti.

I pendini trasmettono una sollecitazione pari alla forza peso corrispondente a questa massa e la distribuiscono sulla lunghezza della corda della curva e non su quella dell’arco della curva (come avviene per il peso proprio del cavo).

Supponiamo che il cavo abbia densità lineare Dcavo, che il ponte abbia densità lineare Dponte e che la curva su cui si dispone il cavo sia descritta da una certa funzione f(x)

Senza andare a scomodare gli amici infinitesimi, supponiamo di dividere il ponte in tanti intervalli ∆x e che il numero di pendini sia X /∆x, garantendo una distribuzione uniforme di tutto il peso. ( X è la lunghezza del ponte, naturalmente).

Possiamo quindi formulare la seguente considerazione:

Quando i cavi sono liberi, in ogni intervallo ∆x il tratto di cavo corrispondente è soggetto a un peso pari a:

∆x f’(x) * dcavo *g (ove g è l’accelerazione di gravità)

Una quantità che varia sensibilmente tra il centro della curva (che nei ponti è simmetrica) e gli estremi.

Quando invece i cavi sono collegati al ponte, la forza peso totale che il tratto di cavo deve reggere è

∆x f’(x) * dcavo g + ∆x f(x) Dponte*g

Essendo, come abbiamo visto, dcavo << Dponte, avremo che in questo secondo caso, a carico, la differenza di forze tra estremi e centro non è più marcata come lo era prima, a vuoto. La distribuzione del peso avviene in modo più diffuso.

Questo, assieme al fatto che i vincoli estremi sono i medesimi a vuoto e a carico, e al fatto che la simmetria della curva rispetto all’asse centrale si conserva, implica una deformazione del tracciato che abbandona il profilo di catenaria per avvicinarsi, risalendo. a quello più “raccolto” della parabola.

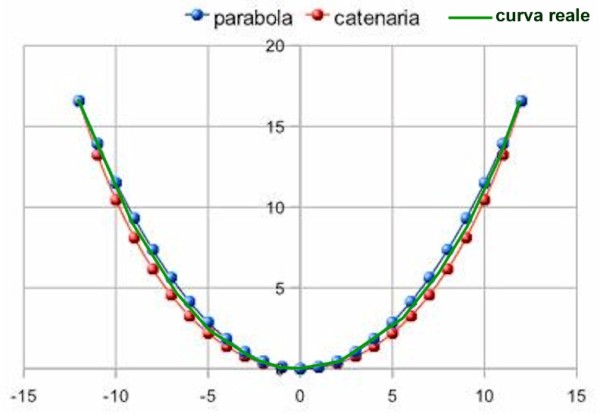
Se i cavi mantenessero rigorosamente la loro lunghezza le curve apparirebbero come nella figura seguente:

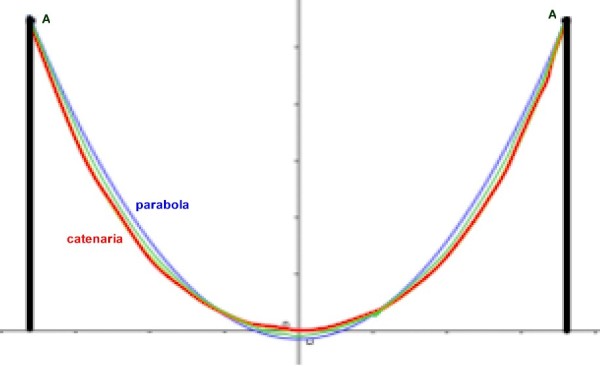
Si noti come, rispetto alla catenaria (linea rossa), la parabola (linea blu) si trova al di sopra nelle zone laterali e al di sotto nella zona centrale. La linea verde, tra le due, è quella più realistica: non è una catenaria e neppure una parabola, pur avendo la loro stessa lunghezza

Ma nella realtà esiste anche un altro effetto da considerare: la elasticità dei cavi, che inevitabilmente si deformano per la sollecitazione del carico, e conseguentemente si allungano.

Resta il fatto che nel mondo reale la curva non è una parabola, per esserlo occorrerebbe che:

1. i cavi fossero fili inestensibili e di massa trascurabile

2. il numero di pendini fosse infinito

3. la loro distribuzione uniforme e il loro tiro identico.

Ma sappiamo bene che nella vita reale non si può avere tutto.

Qui finisce la divagazione di Maurizio e comincia la seconda parte, scritta da Vincenzo.

Da un ponte tibetano ad una autostrada sospesa nel vuoto

Predisponiamo due punti di ancoraggio e colleghiamo ai loro estremi una sottile catenella, leggera ed omogenea per tutta la sua lunghezza.

La catenella, lasciata libera di sistemarsi, ancorata nei due punti più alti, prende la forma di catenaria. Il fatto che sia catenaria (a densità costante), implica che chi comanda la forza peso è la lunghezza ds dell’elemento infinitesimo. Gli intervalli dx corrispondenti sono quelli rossi che, ovviamente, diminuiscono la loro lunghezza allontanandosi da O, mentre i ds rossi rimangono inalterati. La forza peso per ogni ds è sempre la stessa e viene segnata in rosso nel baricentro dell’elemento ds.

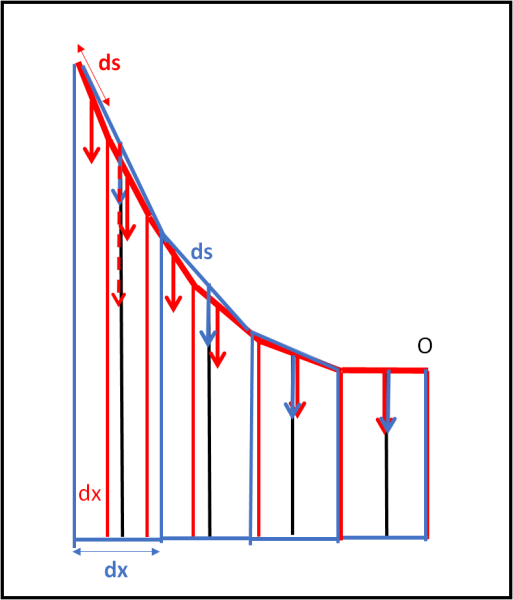
Questo è il classico ponte sospeso in cui si cammina sopra la … catenella.

Le automobili, però, si trovano in netto disagio ad andare su una curva di quel genere e preferiscono di gran lunga un tragitto rettilineo. Il tragitto rettilineo sia quello blu. Immaginiamo di iniziare il confronto con un elemento di strada dx (blu) e un elemento di catenella ds (rosso) che siano orizzontali e quindi coincidano.

Nel caso della strada, chi comanda è la forza peso della strada, dato che la catenella è nettamente più leggera e quindi è costretta a subire le modifiche imposte dalla strada. Dividiamo la strada in dx (blu) tutti uguali in modo che abbiano tutti la stessa forza peso. Notiamo che questa forza peso è nettamente dominante rispetto a quella della catenella che può essere tralasciata. Tuttavia, ogni elemento dx della strada (blu), ha la stessa lunghezza ORIZZONTALE e la stessa forza peso (blu) viene disegnata nel baricentro di ogni elemento.

Per comodità di disegno abbiamo disegnato la forza blu lunga come la forza rossa, ma questo non è vero, dato che la forza blu è ormai l’unica in gioco. Tuttavia, la forza blu viene trasmessa agli elementi della catenella attraverso dei tiranti che la tengono legata all’andamento rettilineo della strada. I tiranti (in nero) sono ovviamente inseriti nei baricentri dei tratti dx della strada. In altre parole, la forza blu è adesso anche la forza peso applicata all’elemento ds della catenella corrispondente all’elemento dx della strada, attraverso i tiranti.

Attenzione, però … A mano a mano che si va verso l’esterno, il singolo elemento dx della strada contiene sempre più elementi ds della catenella. Ne segue che a ogni ds sulla catenella viene associata una forza peso nettamente minore a mano a mano che si va verso l’esterno. A titolo di esempio abbiamo disegnato a tratteggio rosso la forza peso che avrebbe avuto il tratto di catenella compreso tra le due righe blu più esterne se fosse stata libera di sistemarsi da sola (assumendo che la forza peso fosse proprio quella della strada). Si nota la netta differenza tra forza blu applicata all’intero tratto e quella che avrebbe avuto la catenella. La catenella, legata alla strada diminuisce la propria forza peso andando verso l’esterno. Una forza peso, ricordiamo, che è adesso quella trasmessa dai tiranti alla catenella considerata di peso trascurabile.

Ne consegue che è esattamente come se avessimo diminuito la densità della catenella andando verso l’esterno. Essa diventa sempre più leggera ed è proprio ciò che la fa trasformare in parabola.

Un metodo alternativo, se volessimo proprio lasciare la catenella nei ponti sospesi per le automobili, sarebbe quello di compensare questo “alleggerimento”, ossia rendere sempre più pesanti i tratti di strada verso l’imbocco dei ponti. In tal modo aumenterebbe anche il peso della catenella andando verso l’esterno in modo da compensare la perdita di peso e ripristinare il peso sempre uguale per ogni suo tratto ds rosso. Soluzione questa che sarebbe decisamente più costosa e a dir poco assurda per ponti molto lunghi.

E qui si conclude la seconda parte

Al termine di questa doppia lettura dovreste avere qualche idea in più su cosa siano queste due curve: parabola e catenaria, e anche sul fatto che tra questi due archetipi geometrici si frappongano nella realtà infiniti ibridi.