In questo articolo abbiamo introdotto un pò frettolosamente gli spazi di Hilbert, molto utili in  per lo studio di particolari funzioni ( o meglio distribuzioni) che compaiono in fisica. Vediamo adesso di specificare bene gli elementi essenziali che servono per la classificazione e lo studio di tali spazi. Prima di tutti, L'integrale (o misura) di Lebesgue, tramite il quale è possibile definire il prodotto scalare fra due funzioni che sono elementi (vettori)  di uno spazio vettoriale di dimensione infinita. Lasciando da parte il calcolo materiale degli integrali, vedremo quando una funzione è integrabile secondo Lebesgue. Perchè facciamo questo? L'integrale (definito) che tutti conosciamo, e che è anche stato già trattato in questo circolo, è l'integrale (detto anche somma) di Riemann. Questa definizione di integrale fu il primo tentativo, ben riuscito, di formalizzare in una teoria matematica il calcolo di aree sottese da curve o funzioni, e si basa, essenzialmente, sul concetto di rettangolo: costruita una partizione dell’intervallo, l’integrale di una funzione sullo stesso intervallo viene considerato come il limite, al crescere delle partizioni, della somma dell’area dei rettangoli. In sintesi, per dirla in maniera più spicciola, l’integrale di Riemann non è altro che una somma di rettangoli.
Poniamo però l’attenzione dove questo metodo non funziona. Infatti, come primo tentativo di  definire l'integrazione, il metodo di Riemann è soddisfacente, nel senso che permette di calcolare l’area di un’ampia gamma di funzioni. Tuttavia, quest’ampia gamma si scopre poi essere non proprio così ampia: infatti, tra queste, alcune danno particolarmente fastidio a Riemann, e sono quelle troppo discontinue. La funzione di Dirichlet D(x)

non è integrabile secondo Riemann (è infatti troppo discontinua): Lebesgue riesce invece integrarla e a misurarne l’area.

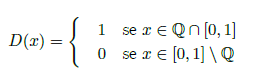
Ma non bisogna uscire dalle funzioni continue per trovarne una non integrabile: ricordiamo che f(x) = log x non risulta integrabile nell’intervallo [0; 1] , perché il limite è infinito e la definizione di Riemann impone la finitezza dell’area.

Lebesgue risolve questi problemi in modo elegante passando per la teoria della misura, di cui abbiamo dato un accenno nel  articolo sull'insieme di Vitali, che  non è un insieme misurabile. Sfrutto perciò parte di quanto esposto in tale articolo per richiamare il concetto di misura. Ricordo, ove non sia specificato direttamente, che il nostro spazio base  sarà sempre l'insieme , ovvero parleremo sempre di insiemi che sono sottoinsiemi di

Per prima cosa definiamo la:

Equidecomponibilità

Parliamo di insiemi.Indichiamo  con questo simbolo  l'unione disgiunta di C,D: .

E' semplicemente l'unione di due insiemi disgiunti, ossia tali che  . Diciamo che due sottoinsiemi A, B sono equidecomponibili se è possibile trovare degli insiemi (disgiunti) A1,..An e dei movimenti rigidi   tali che

Come al solito è più difficile dirlo che farlo: Vediamolo nel piano:nella figura A e B sono degli insiemi apparentemente molto diversi , ma sono equidecomponibili

 

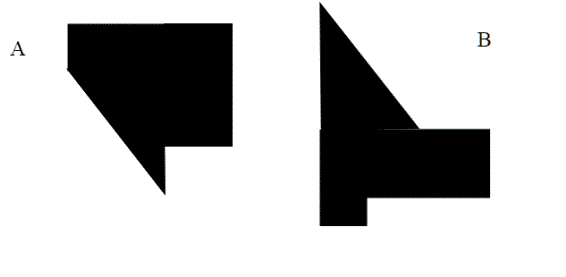
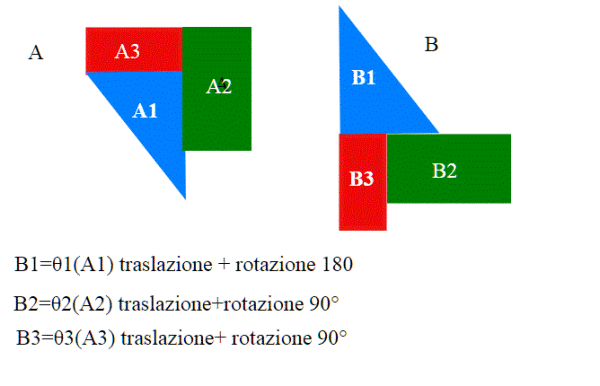
Misurare gli insiemi

Ci proponiamo di definire cos'è la misura di un insieme.  Chiamiamo m tale misura,che agisce sui sottoinsiemi di  .Avremo quindi  una applicazione definita su sottoinsiemi di  a valori in , ovvero sui numeri reali positivi o nulli . La misura  è dunque una funzione  .

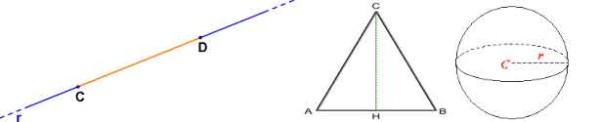
Misurare un segmento è facile, così pure altre semplici figure geometriche nel piano, o i solidi principali nello spazio; In ogni caso otteniamo tramite formule più o meno complesse una lunghezza, una superficie o un volume.

La stessa cosa non si può dire per un insieme qualsiasi di punti, che siano essi in . Non ci preoccupiamo però, per adesso, di come calcolare una tale misura, ossia quali tecniche usare. Ma quali proprietà deve avere una tale misura? Bè, ci farebbe comodo scomporre l'insieme che misuriamo in parti  e poi sommare le misure delle varie parti.  Per applicare tale proprietà, abbiamo proprio introdotto la nozione intuitiva di equidecomponibilità; possiamo pensare di scomporre un insieme A in tanti pezzi A1..An che siano  disgiunti. Cosa  ci aspettiamo da questa misura m?  Che la somma delle misure dei singoli pezzi A1..An sia uguale alla misura dell'unione dei pezzi, e di conseguenza alla misura di A. Scomponiamo A nell' unione di tanti pezzi disgiunti:In modo formale:

; questa scrittura significa che facciamo variare k nell insieme N, che è l'insieme dei numeri naturali. Si parla di unione numerabile. La nostra misura deve avere perciò una "numerabile additività":

Chiaramente il fatto che valga l'additività nel caso di unione numerabile, implica che valga anche quando parliamo di unioni finite. Basta considerare infatti gli Ai tutti vuoti da un certo punto in poi.

Cos'altro deve avere la nostra misura per definirsi valida per i nostri scopi?

Se misuriamo un segmento, la sua misura deve chiaramente coincidere con la misura elementare. Qual'è la misura elementare di[0.1]? E'chiaramente 1. Quindi >0.

Notiamo in particolare che per misurare  insiemi base possiamo parlare di iper rettangoli, ossia intervalli in R, rettangoli in , parallelepipedi in e in generale, appunto insiemi prodotto di intervalli, tanti quanti la dimensione dell'insieme. La definizione formale di  iper-rettangolo , è la seguente:

( notare bene ch gli intervalli sono chiusi)

Si definisce plurirettangolo l’unione di più rettangoli disgiunti:

Si definisce la misura dell’iperrettangolo:
; ovviamente il prodotto delle misure dei lati.
Così come il rettangolo e il parallelepipedo si misurano moltiplicando le dimensioni, nel caso generale di un iperrettangolo la regola non varia.

Possiamo estendere la funzione misura m, aggiungendo ai suoi valori un punto particolare:per quanto ci riguarda, necessitiamo di poter operare con l’infinito, quindi chiameremo retta estesa quella in cui + è considerato al pari di un numero. Questo significa che:

1 una funzione può assumere valore in qualche suo punto, non solo tenderci;
2 degli insiemi possono avere misura infinita.
3 è corretto scrivere un intervallo (per esempio la semiretta positiva) come
[0;+] (con la parentesi chiusa a destra, nel senso che + appartiene all'intervallo, di solito in analisi viene invece escluso).
Il termine ha delle belle proprietà; la prima è che questo è maggiore di ogni altro numero reale scrivibile in altra forma diversa da . Alcune operazione con l’infinito sono le seguenti:
a + =
- b =
-a * = -

Poniamo attenzione all ’ultima espressione. ; non stiamo parlando di limiti in cui si rimane nell'ambito della forma indeterminata.

In tal modo, aggiriamo il fatto che un insieme non sia misurabile se è infinito; la sua misura è l'elemento introdotto, ovvero .

La misura secondo Lebesgue

Siamo adesso pronti per iniziare a definire quelli che, secondo la teoria di Lebesgue, sono insiemi misurabili. Da adesso in poi per misura intenderemo sempre misura secondo Lebesgue.

Definiremo la misura di Lebesgue in più passi, cominciando da quella più semplice di plurirettangolo:

dove gli Ii sono iper-rettangoli

questa è semplicemente la somma delle misure degli Ii:

Passiamo adesso agli insiemi base della topologia, gli aperti e i compatti:

Siano A un insieme aperto e K un compatto, sottoinsiemi di . Si definiscono così le
misure dei due tipi di insieme:

dove sup indica l'estremo superiore e inf l'estremo inferiore.

(per chi non conosce la definizione di estremo superiore  e estremo inferiore può vedere qui;  sostanzialmente però sup rappresenta un valore massimo che però può anche non appartenere all'insieme; inf rappresenta il valore minimo che anche in questo può anche non appartenere all'insieme )

Chiaramente qualcuno mi dirà; da dove saltano fuori queste incomprensibili definizioni?

Pensiamo che sia n=2, ovvero al piano, e a degli esempi su di esso. Pensiamo all'interno di un cerchio, la parte arancione della figura,che è un insieme aperto.

Per misurare, ovvero riempire l'interno del  cerchio, possiamo pensare di prendere dei plurirettangoli (unione disgiunta di rettangoli, sempre più piccoli man mano che ci avviciniamo al confine costituito dalla circonferenza blue). La misura di A è definita come estremo superiore della misura deiplurirettangoli contenuti in A. Pensiamo adesso a K, che è un compatto. Quindi è chiuso e limitato. Nel caso del disegno, esso è costituito da tutto il cerchio. In questo caso prendiamo in considerazione i plurirettangoli che lo contengono; di questi, prendiamo l'estremo inferiore delle misure.

Nel caso di un insieme generico, Lebesgue dà la definizione finale, valida per un insieme qualsiasi:

Dato un sottoinsieme E di , possiamo definire per esso una misura interna ed una esterna:

Osserviamo che qualsiasi sia E,

Chiariamo il senso della definizione con  degli esempi.

Partiamo da n=1, ovvero dalla retta. Un intervallo aperto non è un pluri-rettangolo e nemmeno un iper-rettangolo. Infatti  abbiamo a che fare con intervalli chiusi. Possiamo schematizzare un intervallo aperto così:

a]-------[b.

Consideriamo gli intervalli aperti (che sono particolari plurirettangoli) contenuti in esso; l'estremo superiore delle misure ci dà una misura , che intuitivamente è b-a. Pensiamo adesso ai plurirettangoli che lo contengono, che possono in questo caso essere degli intervalli chiusi. L'estremo inferiore delle misure sarà quella dell'intervallo chiuso [a,b], che è ancora b-a. Da qui vediamo che la definizione data da Lebesgue di misura è una definizione sensata.

Sappiamo invece che un punto, ente primitivo adimensionale, ha logicamente misura nulla.

Ora, detto questo, possiamo finalmente parlare di insiemi misurabili. Date le misure interna ed esterna di un insieme, è logico pensare che, quando queste coincidono, abbiamo a che fare esattamente con la misura di quell’insieme, più o meno come l’area delle partizioni inferiori e superiori per Riemann. A questo punto possiamo dare la definizione di insieme misurabile (secondo Lebesgue):

Un insieme E si dice misurabile secondo Lebesgue se la sua misura interna coincide con l’esterna, ovvero:

Il seguente risultato ci assicura che un insieme E  è misurabile se e solo se per ogni esistono aperto e compatto tali che:

 

Ovvero un insieme sarà misurabile se esisteranno un aperto e un compatto tali che la differenza tra le loro misure è arbitrariamente piccola, ovvero coincide.

La prima conseguenza importante della definizione di misura di Lebesgue, (come  fra l'altro è necessario affinchè soddisfi alla definizione di misura), è che presi comunque degli insiemi E1,...En due a due disgiunti,  allora posto:

si ha:

Poiché possiamo considerare qualsiasi insieme come somma di insiemi disgiunti, la misura di quell’insieme, se è unione di un’infinità numerabile di insiemi, sarà esattamente la somma delle misure degli insiemi. Nel caso infinito, l'insieme E è unione infinita di insiemi disgiunti:

e la somma diventa la somma di una serie:

Sono molte le proprietà che derivano dalla definizione di misura di Lebesgue, comunque questa resta la più importante. La dimostrazione di ciò è conseguenza della definizione, ma noi la prendere per buona.

L'integrale secondo Lebesgue

Ci proponiamo ora di  definire, sfruttando la misura appena definita, di dare una definizione di integrale più potente di quella di Riemann, atta a coprire una più vasta gamma di funzioni, e a cercare di intuire cosa  ha permesso a Lebesgue di cambiare punto di vista sulle aree sottese dalle funzioni. Procedendo gradualmente, iniziamo a vedere delle funzioni semplici da integrare, che chiamiamo appunto funzioni semplici.

Le funzioni semplici

Consideriamo degli insiemi Ei, sottoinsiemi di . Tramite essi, possiamo definire la funzione caratteristica:

Un esempio di funzione caratteristica quando E sia un insieme finito di punti:

 

 

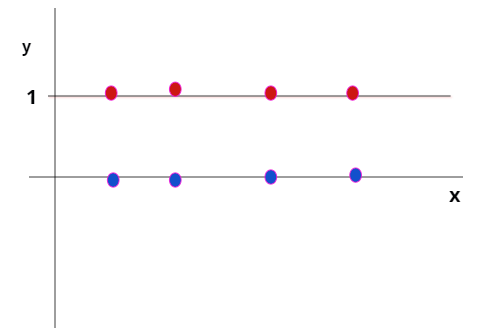
e nel caso :

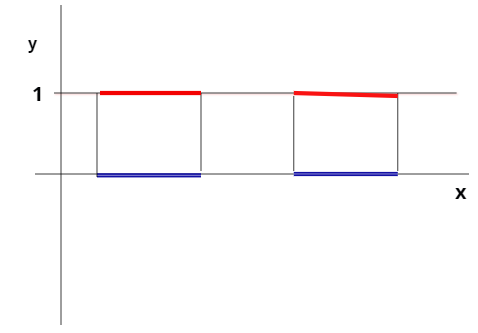
e , supponendo che per i=1,...n siano numeri reali, definiamo anche la funzione semplice:

(attenzione a non confondersi; possiamo esprimerla come sommatoria perchè la funzione assume un solo valore diverso da zero in un certo punto)

 

 

a questo punto è facile definire l'area della funzione semplice, secondo Lebesgue:

Detto questo, possiamo finalmente calcolare l’integrale della funzione di Dirichlet (cosa che non potevamo fare prima con Riemann); essendo definita come:

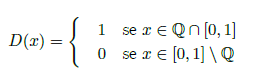
D(x) altro non è che la funzione semplice che ha come insieme di definizione E costituito dai razionali che ci sono in [0,1], che sono pure sempre un insieme numerabile. Quindi è fatto di un insieme  di punti , la cui misura è nulla. Ma sommare infiniti punti di misura zero dà come risultato sempre zero.

Ci fermiamo qui. La prossima volta definiremo l'integrale di Lebesgue per le funzioni qualsiasi, e giustificheremo perchè con tale integrale possiamo costruire gli spazi di Hilbert, così importanti per studiare le funzioni d'onda.