Categorie: Matematica
Tags: algebra elementare calcoli a mente quiz
Scritto da: Vincenzo Zappalà
Commenti:12
Niente computer o calcolatrici ***
Sto vedendo che i quiz semplici mietono poco successo. Va bene... presentiamone uno che potrà interessare anche i più bravi in matematica (ma tutti possono provare a risolverlo). Bisogna calcolare un'espressione SENZA utilizzare computer o calcolatrici, solo carta e penna, un minimo di algebra e ... facilissimi calcoli mentali (basta la tabellina pitagorica).
L'espressione da risolvere è la seguente:
√(500 · 501 · 502 · 503 + 1) = ?
Varie soluzioni, tutte plausibili, le trovate nei commenti.
12 commenti
Consideriamo la seguente espressione:
√[(n-3/2)(n-1/2)(n+1/2)(n+3/2)+1]=
Raggruppiamo per utilizzare i prodotti notevoli:
=√[(n-3/2)(n+3/2)(n-1/2)(n+1/2)+1]=
Utilizziamo (a+b)(a-b)=a²-b²:
=√(n²-9/4)(n²-1/4)+1]=
Moltiplichiamo i polinomi:
=√[n⁴-(1/4)n²-(9/4)n²+9/16+1]=
Sommiamo i termini simili:
=√[n⁴-(5/2)n²+25/16]=
Sotto radice è presente il quadrato di un binomio:
=√[(n²)²-2(5/4)n²+(5/4)²]=√[(n²-5/4)²]=
Semplifichiamo la radice con il quadrato:
=|n²-5/4|=
Supponiamo che sia n²>5/4:
=n²-5/4.
Quindi √[(n-3/2)(n+3/2)(n-1/2)(n+1/2)+1]=n²-5/4. Nel quiz proposto, n-3/2=500, ovvero n=500+3/2. Quindi
√(500·501·502·503+1)=(500+3/2)²-5/4=500²+2·500·3/2+(3/2)²-5/4=250.000+1.500+9/4-5/4=250.000+1.500+1=151.501
Ovviamente, alla fine va corretto "250.000+1.500+1=151.501" in "250.000+1.500+1=251.501", scusate.
Caro Marco,
non ci sarebbe bisogno di rispondere dato che è facile verificare il risultato con una calcolatrice qualsiasi... Bravo!!! Tra un po' te ne offro un altro anche peggiore...
Forse hai fatto perfino dei calcoli più difficili del previsto... aspettiamo a vedere se qualcuno ci prova senza leggere i commenti...
Eh sì, caro Marco... ho controllato meglio i passaggi e devo dirti che l'operazione più difficile da fare è una moltiplicazione di un numero molto piccolo per 3 e il quadrato dello stesso numero (a parte gli zeri...). Comunque, praticamente anche tu hai fatto lo stesso dopo qualche semplificazione di radicali... Ribravo!!!
Confesso, però, di aver barato un po' all'inizio: prima ho fatto il calcolo con il foglio elettronico, poi ho provato a cambiare il valore iniziale, scoprendo che il risultato veniva sempre intero. Così ho capito che c'era qualcosa sotto che non dipendeva dal valore iniziale (500), ma dalla formula in sé; e così, dopo aver verificato in modo induttivo che il radicando era sempre un quadrato, ho cercato dare una dimostrazione deduttiva della cosa.
Ho notato che 2*3*4*5+1=120+1=121 cioè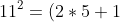^2)
Sembrerebbe che lo stesso valga nel nostro caso. La soluzione indicata da Marco può essere scritta come 500*503+1=250000+1500+1=251501.
A ritroso si può dimostrare sviluppando questa uguaglianza
che risulta vera per ogni x.
Non sono riuscito a trovare lo sviluppo in avanti. Cioè quello che porta da
caro Marco... per il fatto stesso di aver ammesso di avere un po' barato ti meriti comunque il bravo! Però, però, a questo punto sei obbligato fare una semplificazione in più!!!
caro Fabry... dai che ce la puoi fare facilmente...
se pongo 500=x, allora ho:
eseguendo i calcoli sotto radice ottengo:
che posso scrivere come:
i primi tre termini sono i quadrati rispettivamente di x^2, 3x e 1. In tutto ho 6 termini, quindi mi chiedo se per caso non sono davanti al quadrato del trinomio (x^2+3x+1) . E infatti:
Quindi, ricordando la formula del quadrato di un trinomio, ottengo:
ma, allora, la mia radice iniziale diventa semplicemente:
e quindi, sostituendo ora x con 500, ottengo come=(250000+1500+1)=251501)
BRAVO ARTU' !!!! Perfetto...
Vi meritate un quiz un po' più difficile... Complimenti a tutti e tre!!!
Il modo diretto che cercavo potrebbe essere questo. Scrivo per esteso i passaggi del ragionamento.
Dal fatto che anche 2 3 4 5+1=121 posso supporre che ogni espressione nella forma
Vale a dire che sto cercando cosa mettere al posto di p(x) in questa espressione, ammesso che un p(x) possa esistere.
Faccio alcune considerazione sul termine a sinistra.
Il polinomio a sinistra è di 4 grado. Quindi il quadrato di p(x) dovrebbe dare un polinomio di 4 grado. Quindi p(x), se esiste, deve essere un polinomio di 2 grado. Lo scrivo nei termini più generali come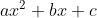
Il termine noto a sinistra è 1. Ne segue che anche il termine noto di p(x) debba essere 1. Solo in questo modo il suo quadrato avrà un termine noto uguale a 1. L'unico termine senza x nel quadrato di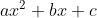
sarà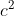 
. Quindi c=1.
Il coefficiente di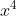
a sinistra è 1. Il coefficiente di 
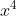nel quadrato di p(x) è 
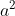. Quindi a=1.
Quindi mi rimane da verificare che esiste un b che soddisfa l'equazione (qui l'incognita è b):
Quindi occorre trovare b tale che 3b=6 e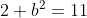
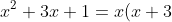. Se b=3 soddisfa tutte e due le ralazioni. Quindi effettivamente il p(x) che cercavo esiste ed è +1)
In effetti dalle considerazione sopra si potrebbe ricavare anche che a=-1 e c=-1. Se scegliessi tutti e due -1 otterrei semplicemenete il caso opposto, cioè b=-1. Ma è ovvio che elevando al quadrato p(x) è indifferente scegliere p(x) o -p(x).
Più interessante è il caso con a=-1 e c=1 o a=1 e c=-1. Prendo il secondo e rifaccio i passaggi come sopra:
Per questo caso non esiste un b adatto. Quindi non esiste una soluzione di questo tipo.
ottima analisi Fabry... anche una semplice espressione può dare luogo a sviluppi più interessanti del previsto.