Una strana somma ***

13/06/20

Una strana somma ***

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:5

Visto il rapido successo dell'ultimo quiz senza l'uso del calcolatore o di una qualsiasi calcolatrice, ve ne propongo subito un altro, forse leggermente più difficile... Magari troverete un metodo più rapido del mio... non mi stupirei di certo!

L'espressione da calcolare è quella che segue (non ho usato il latex visti i problemi che sta causando e ... non solo). La scrittura 3√ sta per radice cubica.

3√(7 +√(5o)) + 3√(7 - √(5o)) = ?

Questa volta, però, niente calcoli preventivi (vero Marco!) ... torniamo ai tempi antichi con carta e penna. Sono sicuro che è un esercizio sempre utile per mantenere le vecchie nozioni e per rendere attivo il cervello!

Forza miei prodi e spero che aumentiate di numero!!!

 

La/e soluzione/i la/e trovate nei commenti!

Articoli correlati

5 commenti

  1. Arturo Lorenzo
    13/06/2020 at 09:34

    \sqrt[3]{7+\sqrt{50}}=\sqrt[3]{7+\sqrt{2*25}}=\sqrt[3]{7+5\sqrt{2}}=\sqrt[3]{1+6+3\sqrt{2}+2\sqrt{2}}=\sqrt[3]{1+6+3\sqrt{2}+\sqrt{8}}=\sqrt[3]{1+6+3\sqrt{2}+(\sqrt{2})^{3}}

    l'espressione finale sotto radice cubica è il cubo del binomio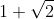 1+\sqrt{2}, quindi la sua radice cubica è proprio il binomio. Stesso ragionamento per l'altra radice cubica della somma, in quel caso il risultato è il binomio. In definitiva, il risultato della somma data è 2.

  2. Arturo Lorenzo
    13/06/2020 at 09:35

    scusate, è saltata l'espressione del secondo binomio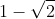  1-\sqrt{2}

  3. Vincenzo Zappalà
    13/06/2020 at 11:10

    va bene, va bene... devo proprio impostare come quiz una soluzione non ancora trovata delle equazioni di Einstein!!! :mrgreen:

  4. Fabrizio
    13/06/2020 at 11:55

    Per non riscrivere l'espressioni con le radici gli assegno un nome

    a=\sqrt[3]{7+\sqrt{50}}\;\; e\;\; b=\sqrt[3]{7-\sqrt{50}}

    L'obiettivo è trovare il modo di eliminare le radici dalle espressioni.

    Per questo possono tornare comode queste relazioni.

    a b=-1                infatti  \small ab=\sqrt[3]{7+\sqrt{50}}\,\sqrt[3]{7-\sqrt{50}}=\sqrt[3]{(7+\sqrt{50})(7-\sqrt{50}})=\sqrt[3]{49-50}=-1

    \mathbf{a^3+b^3=14}            infatti \small a^3+b^3=(\sqrt[3]{7+\sqrt{50}})^3+(\sqrt[3]{7-\sqrt{50}})^3=7+\sqrt{50}+7-\sqrt{50}=14

    Entrambe queste due espressioni compaiono nel cubo di a+b

    (a+b)^3=a^3+b^3+3a^2b+3ab^2   (triangolo di tartaglia)

    Una è evidente, l'altra bisogna estrarla dagli ultimi due termini che hanno in comune proprio ab

    (a+b)^3=a^3+b^3+3a^2b+3ab^2=\mathbf{a^3+b^3}+3(a+b)\mathbf{ab}=14-3(a+b)

    Sembrerebbe di essere punto e a capo. Mi ritrovo sempre con a+b di mezzo che è propri quello che cerco.

    Però questa è anche una equazione nella nostra incognita (a+b) che posso risolvere.

    x^3+3x=14

    Senza ricorrere alle formule generali si vede che una soluzione è x=2 (trascuro le soluzioni complesse)

    2^3+3\,2=8+6=14

    Quindi   a+b=\sqrt[3]{7+\sqrt{50}}+\sqrt[3]{7-\sqrt{50}}=2

     

  5. Vincenzo Zappalà
    13/06/2020 at 14:21

    siete veramente magnifici e pieni di fantasia creativa!!!

    Se vi diverte continuo... ne ho trovato parecchie...

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.