Concludiamo l'avventura di Tarzan (iniziata QUI) sia matematicamente che geometricamente, permettendo anche una costruzione meccanica (roba da ingegneri della giungla...)

Prima parte - calcolo della equazione della traiettoria + massimizzazione della gittata 

Con riferimento al problema del "volo" di Tarzan,  si propone un semplice metodo per  determinare  l'angolo di distacco dalla liana (pendolo) che consente di realizzare il volo parabolico ottimale,  ossia quello la cui traiettoria si conclude nel  punto di atterraggio più distante.

Consiglio di ricopiare a mano questa figura (non di stamparla) perché in questo modo si prende maggiore coscienza del significato di ciascun elemento. Inoltre, nel corso della lettura, si potrà sempre consultare il proprio disegno e ritrovare gli elementi descritti senza dover riposizionare  l'immagine sullo schermo. L'espediente di aprire una seconda finestra per vedere in essa  la figura mentre si legge, a volte utile, riduce comunque lo spazio di lettura  ed è meno pratica. Anche se siamo circondati da mille tecnologie non siamo obbligati a rinunciare sistematicamente al piacere di scrivere e disegnare a mano.

Teniamo in allenamento le nostre abilità psicomotorie.  Evitiamo di perderle.

Dati noti

T = posizione iniziale = altezza della piattaforma da cui si lancia Tarzan

C=punto di  ancoraggio della liana =  Centro di sospensione pendolo alla stessa quota di T

R = lunghezza della liana = Raggio del pendolo

Dati fondamentali per trovare la soluzione

S= punto di Stacco e ORIGINE PRESCELTA PER IL SISTEMA DI RIFERIMENTO DELLE COORDINATE  X Y   

S' = punto simmetrico a S (rispetto al Vertice)

O= punto di partenza della misura   per la distanza D

A= punto di Arrivo

In molti casi vi sono più dati di contorno nel problema, oltre a quelli veramente fondamentali. Per non complicare la soluzione meglio evitare di prenderli in considerazione.

Altri dati ( non rilevanti)  che possono essere determinati  in base alle relazioni esistenti nel sistema

P = Punto equilibrio del pendolo

a=altezza dal terreno alla estremità della liana sulla sponda del fiume (rispetto alla retta OA)  vale la relazione   ( a = T - R)

La =  distanza coperta in oscillazione

Lp = distanza  coperta in volo

M = punto medio tra S e S'

V=vertice parabola

Valori incogniti da calcolare 

=  variabile di controllo da determinare in funzione della massimizzazione di D

D= distanza massima ottenibile

Conoscenze preliminari necessarie  per la comprensione del metodo usato

Si danno per conosciute le seguenti relazioni:

L' equazione di una generica parabola passante per l'origine delle coordinate

La velocità in un punto del cerchio di oscillazione del pendolo espressa in funzione del valore di angolo

(derivabile dal bilancio energetico tra energia potenziale e cinetica          )

La espressione della gittata, ossia la  distanza coperta dal punto di lancio al punto simmetrico allo stesso livello  (rispettivamente S e S') da un proiettile lanciato nel punto di origine degli assi con velocità e angolo di alzo noti.

Procedimento proposto per la soluzione del problema

La continuità del moto nel punto S  (di stacco) che coincide con l'origine del sistema di riferimento, impone che la tangente sia comune al cerchio e alla parabola (l'angolo che forma con l'asse x  non è altro che  ) e che la velocità tangenziale in quel punto coincida con la velocità di lancio.

Sostituiamo pertanto l'espressione della velocità V nella  espressione della gittata.

SS' =       Gittata = Ascissa del punto S'  (di ricaduta al livello di partenza)

L' ordinata del punto S'   è  nulla,  per il fatto che  il punto appartiene all'asse delle x.  Quindi il punto S' ha le seguenti coordinate:

Dato che l'equazione della parabola contiene solo due parametri:  a, b  non è sufficiente la conoscenza di un solo punto di passaggio per  determinarli univocamente.  Ma sapendo che il coefficiente angolare della tangente alla traiettoria nel punto S,  di origine degli assi  e di continuità   tra cerchio e parabola,   è semplicemente           si determina immediatamente  il valore del coefficiente  b   del  monomio di primo grado. Infatti, derivando la  equazione parabolica   ,  otteniamo     e imponendo  il valore Zero per la x ,  si ha   y' = b  = tan

Resta solo da ricavare il valore del coefficiente a, sostituendo  nella equazione il valore trovato per b  e imponendo il passaggio per il punto S':

    da cui  ricavo il coefficiente a

Scriviamo quindi    l'equazione della parabola   sostituendo nella sua espressione generica i valori di a e di b.

Riassumendo: Ciascun punto sul cerchio di oscillazione   è associato ad un solo valore possibile dell'angolo     e (avendo fissato il punto T)  ad un solo valore possibile del vettore velocità.  Il punto di ricaduta  alla stessa quota è univoco.   In altre parole, esiste una sola traiettoria parabolica che si raccorda al punto S  sul cerchio, e la sua equazione è quella che abbiamo appena ricavato.

Passiamo ora al calcolo della distanza  OA =  D   riportando la figura precedente, per comodità di lettura.

Scriviamo le coordinate del punto     abbiamo messo in evidenza i segni negativi .

Per quanto riguarda le coordinate del punto di arrivo  A,  che appartiene alla parabola, dobbiamo imporre il valore  noto della sua ordinata  ( uguale a quello del punto O)  e ricavare la x.

      risolvo questa equazione di secondo grado in x trovando la radice maggiore che riguarda il punto A.

La distanza D vale  la differenza tra le due ascisse di A e di O

Per trovare il valore della variabile di controllo 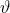  che massimizza la distanza D occorre derivare questa equazione, uguagliarla a zero, e ricavare il corrispondente valore di 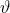. Successivamente il valore trovato va inserito nella equazione per trovare la misura della distanza massima cercata.

A parte la eventuale difficoltà di calcolo della derivata, l'equazione ottenuta è trascendente e il valore di   che la azzera è di difficile estrazione.

La rappresentazione grafica della derivata consentirebbe però di individuare il punto di intersezione  con l'asse , ossia il valore dell'angolo a cui corrisponde il valore di distanza massima.

In alternativa è possibile studiare graficamente  l'andamento della funzione nell'intervallo di    tra 0° e 50°  per individuarne l'angolo con cui si raggiunge la massima distanza. Tale angolo sarà di certo inferiore a 45°.

Dato uno specifico valore della lunghezza R si trova nel punto di massimo  la coppia  angolo  gittata    

Se si modifica il valore di R si ottengono varie curve e si nota che maggiore è R , maggiore sarà la distanza massima raggiungibile.

Il valore più grande di tutti si ottiene con un R pari alla distanza della pedana di lancio dal terreno   (R=T )

Questa  famiglia di curve consente  di  "vedere" (anziché calcolare con precisione analitica, tramite la  derivata)   quale angolo di stacco produce il risultato ottimale, per ciascuna liana utilizzata tra le varie misure  di R, da 7 a 10 metri.

Le gittate ottimali variano tra  19 e 24 metri, con angoli di stacco compresi tra 36° e  41°.

In generale si ritiene che questo metodo per individuare il massimo non sia sufficientemente preciso, ma semplicemente usando la equazione excel che ha prodotto questi grafici, in un intervallo di valori prossimi al massimo, è facile stimare con alta precisione angolo critico e gittata corrispondente

Questo esempio, su una delle curve, (blu)  lo dimostra:  Su una gittata di 24 metri l'errore di valutazione è inferiore a 1 cm.

Il valore di angolo è determinato con 0,5° di approssimazione, ma l'indeterminatezza si può ridurre  a piacere iterando l'analisi su intervalli più ristretti.

Vederemo prossimamente come è possibile determinare con una costruzione grafica il punto di arrivo A.

_________________________________________________________________________________________________

Seconda parte  - Costruzione grafica per determinare il punto di arrivo  A  (dato l'angolo)

La curva completa inizia con un arco semicircolare che conduce dal punto in cui Tarzan si getta dalla rupe avvinghiato alla liana, fino a giungere a livello del suolo, in riva al fiume.
La traversata sopra le acque inizia qui, dapprima trattenuto dalla liana, sempre lungo la medesima circonferenza, fino al punto in cui si stacca ed inizia il tratto in volo libero. In quel preciso momento la sua traiettoria diventa parabolica, fino a concludersi nel punto di atterraggio A, sulla sponda opposta del fiume.

l'equazione della traiettoria che avevamo ricavato,  nella classica forma  cartesiana       ,   è la seguente:

La parabola passa per l'origine degli assi e i coefficienti  a e b  hanno i seguenti valori:

         ( in cui il segno negativo indica che la parabola ha concavità rivolta verso il basso)

Gli elementi geometrici fondamentali della parabola, descritta come luogo dei punti equidistanti dal fuoco e dalla direttrice,  facendo riferimento ai coefficienti a , b  sono:

il discriminante 

l' asse                     

il vertice           

il fuoco               

la direttrice       

Con i valori di a e di b che abbiamo individuato, questi elementi assumono la forma seguente:

       (il coefficiente   c    è assente, perché la parabola passa per l'origine)

Trasferiamo in un grafico questi elementi e riconosciamo le relazioni  geometriche e trigonometriche che esistono tra di essi

Il raggio  CS = r   si proietta verticalmente in   CH = r cosθ  e  orizzontalmente in  HS= r senθ come indicato in figura.

La proiezione di r cosθ sul segmento CS non è altro che r cos²θe la proiezione di quest'ultimo sul segmento CH  ci dà r cosθ³.

La proiezione di  r cos sulla perpendicolare al raggio CS , passante per il punto H, fornisce r cosθ senθ  e  l'ulteriore proiezione di esso sulla verticale ci dà  r cosθ sen²θ  ( si veda la  corrispondente dicitura sul lato destro oltre la parabola), mentre sull'asse x  ci dà r cos²θ senθ.

Quest'ultimo segmento, di lunghezza r cos²θ senθ riportato 2 volte dall'origine, lungo l'asse x, individua la posizione dell'asse della parabola.

Tutti i punti alla sinistra di questo asse di simmetria hanno un corrispondente punto speculare a destra. In particolare il punto S' è speculare di S.

Basta quindi riportare altre 2 volte il segmento r cos² sen per individuare S'    La distanza S S' non è altro che la "gittata"

L'altro segmento che abbiamo ottenuto, ossia   r cosθ sen²θcorrisponde esattamente alla ordinata del vertice della parabola, la quota massima.

Ma il nostro interesse è "focalizzato" sul punto A. Quello è il traguardo da raggiungere, e si trova sulla parabola, ma non sappiamo esattamente dove.

Analiticamente potremmo calcolare la sua ascissa, dato che conosciamo la sua ordinata, ma graficamente come si può procedere?

Ebbene, per la definizione di parabola come Luogo di Punti, conoscendo il Fuoco e la Direttrice siamo in grado di costruire qualsiasi punto della curva, compreso il nostro punto A.

Vediamo allora di disporre sul disegno anche questi due fondamentali elementi; il Fuoco e la Direttrice. Dato che la parabola ha concavità verso il basso , la direttrice sarà sopra al fuoco (speriamo che non si bruci troppo).

Posizioniamo prima  la Direttrice:   è  la retta orizzontale  y= r cosθ alla stessa quota del punto C

Ora mettiamo il fuoco sotto la direttrice in base alle sue coordinate. Risulterà appartenere all'asse di simmetria e si troverà sotto il vertice V, in posizione simmetrica alla direttrice.

La distanza della Direttrice dal Fuoco è  la differenza delle ordinate  r cosθ -  (r cosθ- 2 r  cos³θ)  =  2 r cos³θ

Verifichiamo rapidamente la simmetria di questi due elementi rispetto al vertice.  L'ordinata del vertice è  r cosθ sen²θ   sommando ad essa  la quantità  r  cos³θ   abbiamo: r cosθ  sen²θ  + r cos³θ  =  r cosθ (sen²θ +cos²θ) = r cosθ,  che corrisponde alla quota della Direttrice.

Sottraendo invece alla ordinata del vertice  V   la quantità  r cos³θ   abbiamo l'espressione  seguente:   r cosθ senθ² - r cos³θ= r cosθ (senθ² - cosθ²) = r cosθ (1-2 cosθ²)  = r cosθ - 2 r cosθ³   che è proprio l'ordinata del Fuoco.

Tornando alla figura non resta che impugnare il compasso e, con apertura pari ad A A' (distanza tra la direttrice e la retta orizzontale per MA) e centro nel Fuoco F, tracciare l'arco che va ad intersecare la MA, per identificare finalmente il punto A di Arrivo. La retta MA , ricordiamolo, è il livello del terreno e della superficie dell'acqua del fiume, la intersezione in A con la traiettoria parabolica significa: atterraggio concluso.

In questa costruzione abbiamo determinato graficamente il punto di arrivo senza eseguire calcoli, ma solo osservando segmenti e relazioni tra di essi.
Tarzan una volta scelta la rupe da cui lanciarsi e la liana da utilizzare, ha ancora una importante decisione da prendere: il momento in cui abbandonare la presa, ossia l'angolo di alzo del suo volo per andare il più lontano possibile. Non è con questa costruzione che ottiene una risposta ma, una volta determinato questo angolo e la distanza ottimale raggiungibile, utilizzando i metodi visti in precedenza, è in grado di tracciare esattamente la sua traiettoria semplicemente con riga e compasso

Procedura di costruzione manuale della posizione del punto A

Vedremo prossimamente come sia possibile automatizzare meccanicamente questa costruzione

______________________________________________________________________________________________________

Terza parte  - Costruzione meccanica per determinare il punto di arrivo  A  (dato l'angolo)

Come trovare l’angolo di distacco che massimizza la distanza del lancio con la liana (Senza derivate)

Un semplice dispositivo meccanico fornisce la lettura dell’angolo cercato attraverso l’esplorazione esaustiva e automatica dei risultati ottenuti, occorre solo ruotare da 0° a 90° una asticciola (CS).

Sopra il piano quadrettato vengono assemblati i componenti del sistema.

Nei 4 punti C, C', M, M' ci sono incastri o saldature che creano un telaio rettangolare rigido, i cui lati orizzontali sono denominati “Direttrice”, “terreno”

Le due aste orizzontali denominate “vertice”, “gittata” terminano con due manicotti al cui interno possono scorrere i lati verticali del rettangolo. Queste due aste sono libere di traslare in verticale mantenendo il loro assetto orizzontale.

L’asta verticale che passa per i punti D V F è l'asse della parabola. Può traslare orizzontalmente mantenendo il suo assetto verticale grazie ai due manicotti agli estremi in cui scorrono le aste “Direttrice”, “terreno”.

La struttura costituita dai 3 lati MQ   Q M"   M"M   è bloccata nei suoi 3 vertici  ed il binario circolare di un quarto di cerchio, ancorato nei punti da M a M' viene percorso dal punto S di modo che l’asticciola che costituisce il raggio CS, ruotando, modifichi l'angolo teta.

L'asse Y è dotato ai suoi estremi di due manicotti, al cui interno scorrono la linea della "Direttrice" e quella del "terreno" di modo che Y è libero di traslare orizzontalmente mantenendo l’assetto verticale.

Nel punto C, centro del cerchio è incernierato il raggio rotante CS, o raggio “motore”. Nel punto H è incernierata un'asta lunga come il raggio.

Questi due elementi si incrociano nel punto O in cui è posizionata una crociera di quattro manicotti girevoli su uno stesso asse verticale. Sono 4 elementi tubolari, liberi al loro interno e vincolati tra loro con la libertà di ruotare di 360° reciprocamente.

Il raggio motore scorre nel manicotto orientato CS.

L’asta incernierata in H, di lunghezza pari al raggio, scorre nel manicotto orientato HO.

Nei due restanti bracci della crociera scorrono: L'asta del "vertice " e un’ultima asta verticale di lunghezza pari al raggio, fissata ad un manicotto in cui scorre l’asta della “gittata” Sul lato più basso questa asta si estende ulteriormente, fino a terra, ove termina con un manicotto in cui scorre l’asta “terreno”.

Allo spostarsi del punto S, estremo del raggio motore, lungo il binario circolare, vengono messi in moto i seguenti elementi: l’asse X, l’asse Y,  le tre aste accoppiate al raggio nel punto O , ossia l’asta del “vertice”, l’asta verticale e quella inclinata.

Riassumendo: all'interno della cornice fissa, gli altri elementi sono mobili e consentono di riprodurre tutte le posizioni dei componenti come si verrebbero a disporre eseguendo la corrispondente costruzione grafica, al variare dell'angolo di rotazione del raggio.

Abbiamo fin qui analizzato i componenti sul lato sinistro della figura e compreso i loro spostamenti relativi conseguenti al muoversi del raggio. Sul lato destro non si sono però prodotti spostamenti di sorta: gli elementi Asse della parabola e asta di collegamento tra Fuoco e punto A non sono ancora connessi al resto della struttura.

Per completare il sistema occorre quindi "comandare" la posizione dell'asse della parabola e la posizione del punto F, il suo fuoco, in modo coordinato con la rotazione del raggio motore.

La fase di completamento dei collegamenti è rappresentata in questa seconda figura.

I tre vincoli da realizzare dovranno garantire il rispetto delle seguenti relazioni:

1. il posizionamento dell'asse della parabola, che dipende dalla misura del segmento denominato in figura: "r cosθ²senθ", precisamente la distanza tra il punto S e l'asse deve valere il doppio di rcosθ²senθ.
2. il posizionamento del Fuoco F della parabola, tale che la distanza DF sia il doppio della distanza DV. Questo equivale a dire che il vertice V risulta sempre intermedio Tra la “Direttrice” e il “Fuoco”.
3. il punto estremo dell'asta FA, di lunghezza pari alla distanza dalla “Direttrice” ossia CM', che deve appartenere alla linea del "terreno".

L'ultimo di questi vincoli si realizza facilmente inserendo agli estremi di FA due manicotti con cerniera in cui scorrono rispettivamente l’asta dell’asse e del terreno.

Per soddisfare i punti 1 e 2 occorre aggiungere una struttura che duplichi la traslazione di un’asta e la trasmetta ad un’altra asta parallela. Per essere più precisi, occorreranno due di queste strutture: una per l’accoppiamento di movimentazione dell’asta “Asse” e una per la movimentazione del punto “Fuoco”.

Vediamo subito come procedere per la movimentazione dell’Asse della parabola

Sul lato sinistro inseriamo sullo stesso perno, perpendicolare al piano di montaggio, due ruote vincolate a ruotare insieme, una di diametro doppio dell’altra. Poniamo sul lato opposto una identica coppia di ruote.

Disponiamo un cavo ad anello in modo che aderisca strettamente alle circonferenze delle ruote più piccole ed un altro che circondi le ruote più grandi. La rotazione comune implica una velocità tangenziale della ruota maggiore doppia di quella della ruota minore, quindi una lunghezza di transito del cavo esterno doppia di quello interno. Non vi deve essere alcun slittamento tra cinghie e pulegge, ovvero cavi e ruote.

Non ci resta che collegare i punti che devono muoversi in sintonia ai rispettivi cavi: quello dell’asse della parabola sarà collegato al cavo esterno, quello dell’asta verticale, che passa per O, al cavo interno.

In modo del tutto simile con una seconda struttura gemella, visibile sul lato destro della figura, potremo collegare l’asta del “vertice” al cavo interno e il Fuoco al cavo esterno, con una opportuna asta vincolata ad un manicotto in cui scorre l’asta CM’, ottenendo la movimentazione necessaria.

Adesso tutti i componenti si spostano in sincronia, con precisi accoppiamenti che riproducono la legge del moto. Quando il raggio motore viene messo in rotazione tutte le aste si spostano traslando e ruotando per generare la posizione istantanea del punto A al variare dell’angolo Teta.

Non resta che introdurre una memoria nel sistema per registrare il massimo valore di ascissa raggiunto dal punto A. Questo si realizza immediatamente posizionando una lancetta indicatrice su un manicotto, in cui scorre l’asta “terreno”, contiguo al manicotto di A. Durante la prima fase di crescita dell’angolo Teta la lancetta verrà sospinta verso destra; raggiunto il massimo, inizierà un arretramento di A ma non, essendovi alcun vincolo, la lancetta rimarrà nella posizione di “massimo” raggiunta, fornendo la lettura desiderata.

Il meccanismo riproduce l’insieme di tutti i lanci e fornisce la risposta che, in via analitica, avrebbe richiesto il calcolo di derivate e la soluzione di una equazione trascendente. Si può certamente costruire anche nel cuore della gingla, con canne di bambù di vario diametro e lunghezza da cui ricavare aste, manicotti e cerniere, con corde di fibra vegetale e ruote ricavate sezionando tronchi di grossi rami. Una passeggiata.