Questa serie di articoli, relativi a formule trigonometriche di uso non sempre comune, ma che non è raro trovare in molte dimostrazioni, sarebbe di pura didattica. In particolare risponde all'incertezza giustificata di Franco nel quiz su Giggiriva. Tuttavia, sperando di dare spunto a chi ha voglia di mettersi alla prova, li imposterò come una specie di "quiz".
L'impostazione tipo "quiz" si divide in due parti. Nella prima scrivo le formule relative all'articolo in questione, nella seconda passo alla dimostrazione, lasciandola però nascosta per qualche giorno, in modo che, se qualcuno avesse voglia di provarci da solo, non venga distratto da ciò che viene scritto dopo.
Diamo per scontato il significato delle funzioni trigonometriche principali e alcune celebri relazioni (QUI, QUI e anche QUI) e vediamo di affrontare quelle già a volte usate, ma mai -forse- descritte in modo esauriente.
Quante volte l'abbiamo usata direttamente o indirettamente? Ricavarla è veramente semplicissimo e basta applicare il teorema di Pitagora, dato che il raggio del cerchio è proprio uguale a 1. A volte la relazione (1) viene usata per eliminare una delle due funzioni da una certa espressione. E' sufficiente scrivere la (1) nei seguenti modi:
Queste sono formule importantissime e usate comunemente. Esse permettono di esprimere le funzioni trigonometriche della differenza o somma di angoli solo con le funzioni dei singoli angoli:
Passiamo alla dimostrazione (con mascherina). Come ulteriore aiuto vi invito a rileggere questo capitolo del corso di matematica.
Iniziamo proprio a dimostrare la formula del coseno della differenza di due angoli. Utilizziamo il nostro cerchio trigonometrico (raggio unitario). Consideriamo tutto nel primo quadrante, ma la cosa non ha assolutamente importanza.
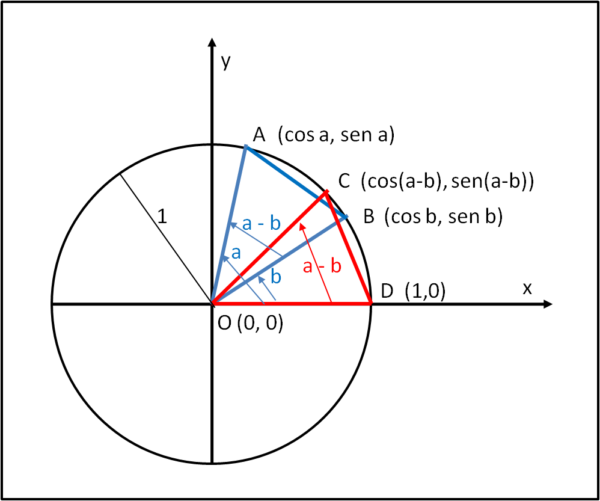
L'angolo a e l'angolo b sono delimitati dall'asse x e dai segmenti OA e OB, rispettivamente. L'angolo AOB è proprio l'angolo differenza (a - b). Ruotiamo questo angolo in modo da portare il lato OB a coincidere con OD. OA va, allora, a coincidere con OC. Abbiamo così individuato quattro punti sulla circonferenza di centro O. Per come sono stati costruiti l'angolo AOB deve essere uguale a COD. Ne segue che, se sono uguali gli angoli al centro, devono anche essere uguali le corde AB e CD. Non ci resta che scrivere le distanze AB e CD e uguagliarle tra loro. Vediamo, allora, le coordinate di questi 4 punti:
A (cos a, sen a)
B (cos b, sen b)
C (cos(a - b), sen (a - b))
D (1, 0)
Ricordiamo che la distanza tra due punti P1 (x1, y1) e P2(x2, y2) è data da:
d2 = (x2 - x1)2 + (y2 - y1)2
Nel nostro caso:
AB2 = (cos a - cos b)2 + (sen a - sen b)2
CD2 = (cos(a -b) - 1)2 + sen2(a - b)
Esplicitiamo i quadrati e uguagliamo
cos2a + cos2b - 2cos a · cos b + sen2a + sen2b - 2sena · senb = cos2(a - b) + 1 - 2 cos(a - b) + sen2(a - b)
La somma delle funzioni in grassetto, in nero, in rosso e in blu danno come risultato 1, per cui l'espressione diventa:
1 - 2cos a · cos b + 1 - 2sena · senb = 1 + 1 - 2 cos(a - b)
semplificando, abbiamo proprio la formula che cercavamo:
cos(a - b) = cos a · cos b + sen a · sen b
Potremmo ripetere lo stesso procedimento anche per le altre funzioni, ma se ne può fare tranquillamente a meno. Basta ricordare quanto valgono le funzioni degli stessi angoli negativi...
sen(-a) = - sen a
cos(-a) = cos a
E le funzioni di (90 + a)
sen (90 + a) = cos a
cos (90 + a) = - sen a
Nella formula del coseno della differenza, possiamo inserire al posto di b l'angolo (-b)
cos(a - (-b)) = cos a · cos(-b) + sena · sen(-b)
cos(a + b) = cos a cos b - sen a sen b
che è proprio la formula relativa alla somma di due angoli.
Prendiamo adesso l'angolo a uguale a (90 + a)
cos(a + 90 - b) = cos (90 + a) · cos b + sen (90 + a) · sen b
cos(90 + (a - b)) = cos (90 + a) · cos b + sen (90 +a) · sen b
- sen(a - b) = - sen a · cos b + cos a · sen b
sen(a - b) = sen a · cos b - cos a · sen b
E abbiamo il seno della differenza di due angoli.
Usando quest'ultima e cambiando b in (-b)
sen(a - (- b)) = sen a · cos(-b) - cos a · sen(-b)
sen(a +b) = sen a · cos b + cos a · sen b
Che è la formula del seno della somma di due angoli
Passiamo, infine, alle formule relative alla tangente, ricordando che tan a = sen a/cos a
Per far ciò, dobbiamo imporre che a, b, (a+b) e (a -b) NON siano uguali a 0° o a 180° per evitare valori che vadano a infinito.
tan(a - b) = sen(a -b)/cos(a - b)
esplicitando...
tan(a - b) = (sen a · cos b - cos a · sen b)/(cos a · cos b + sen a · sen b)
dividendo ogni fattore sopra e sotto per cos a · cos b (possiamo farlo perché abbiamo imposto a e b diversi da 90° e 180°), abbiamo:
tan(a - b) = (sen a · cos b/(cos a cos b) - cos a · sen b/(cos a cos b))/(cos a · cos b/(cos a cos b) + sen a · sen b/(cos a cos b))
Semplificando...
tan(a - b) = (tan a - tan b)/(1 + tan a · tan b)
che è la formula relativa alla differenza dei due angoli
Considerando adesso
tan (a + b) = sen (a + b)/cos(a + b) = (sen a · cos b + cos a · sen b)/(cos a · cos b - sen a · sen b
e dividendo nuovamente ogni fattore per cos a · cos b
tan(a + b) = (sen a · cos b/(cos a cos b) + cos a · sen b/(cos a cos b))/(cos a · cos b/(cos a cos b) - sen a · sen b/(cos a cos b))
tan (a + b) = (tan a + tan b)/(1 - tan a · tan b)
che è la formula relativa alla somma degli angoli.







2 commenti
Visto che sono la "causa" involontaria della tua fatica, dovrò studiare..
In quanto ad Euclide e Giggiriva...sono fermo.
carissimo Franco...
beh ... ti tocca! Ho già inserito la soluzione per Giggiriva, ma tu non leggerla e pensa a una circonferenza per te punti...
