Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

 

(articolo pubblicato il 8/11/2013)

Tutti avranno sentito parlare di precessione almeno una volta. Essa viene citata sia quando di parla di spostamento della stella polare come indicatrice della direzione del polo nord sia quando si discute sul cambiamento delle costellazioni dello zodiaco sia, a volte, delle coordinate delle stelle. In qualche modo si parla di precessione solo per i suoi effetti, ma non riguardo alla sua vera ragione fisica. Eppure, la osserviamo sempre quando facciamo girare una trottola e i telescopi spaziali non potrebbero puntare esattamente gli oggetti celesti senza "trottole" molto speciali.

Ci sono vari modi per descrivere il moto di precessione. Normalmente, si parla di quello dell’asse terrestre e degli effetti che provoca. Ne segue che vengono solitamente riportati i valori numerici che la precessione comporta, ma si parla ben poco del fenomeno fisico che la causa. I numeri li possiamo trovare un po’ ovunque. Preferisco, quindi, dedicarmi al concetto generale e trascurare le ricadute varie e la loro quantificazione numerica.

Vi sono, però, vari livelli per affrontare la precessione e sua “figlia”, la nutazione: quello più empirico (1), basato su un’analisi molto qualitativa, priva di formule, che può dare solo un’idea del meccanismo e che lascia molte considerazioni nel vago; quella un po' più tecnica (2) che analizza le variabili fisiche che giocano un ruolo decisivo, ma ancora a livello qualitativo. Infine, quella veramente rigorosa (3) che, ovviamente, deve fare uso di formule matematiche, anche se di livello molto basso, e di una conoscenza di base di certi parametri essenziali. Essa permette di quantificare la precessione e, quindi, di calcolarla in base alle condizioni di partenza, caso per caso. La precessione, però, e non solo i suoi effetti osservabili! E qui sta la vera differenza con i soliti testi descrittivi.

Per far contenti sia i lettori meno esperti sia quelli più  competenti, ho deciso di trattare l’argomento in tutti e tre i modi  Ecco perché compaiono dopo il titolo sia uno, sia due, sia tre asterischi.

Userò una trottola generica per le spiegazioni, lasciando l’applicazione al nostro pianeta nelle conclusioni finali, che andranno bene per tutti i gruppi di appassionati. Riguardo alla nutazione, per le sue indubbie complicazioni di calcolo, mi affiderò solo a una descrizione elementare e intuitiva, che però basterà a chiarire la cattiva informazione che si dà normalmente su di lei.

Si legge, infatti, che essa dipende essenzialmente dalla Luna. Questo non è esatto. La realtà fisica del Sole e della Luna, con le loro distanze, masse e posizioni relative, incide su entrambi i fenomeni (precessione e nutazione) e, al limite, causa delle discordanze rispetto a una trattazione teorica. Tuttavia, la nutazione esiste, comunque, anche se ci si riferisce alla classica trottola, in cui non partecipano né Sole né Luna, ma solo la forza di gravità della trottola. Come vedremo essa è un effetto del “secondo ordine”, ma le sue cause sono la precessione e la rotazione intorno a un asse, senza alcun bisogno di altre particolarità perturbatrici. Non sfuggirà, inoltre, ai più preparati, che la precessione è qualcosa che richiama perfettamente la marea luni-solare e che ci porta al giroscopio e alla sua fondamentale utilità nel mantenere la stabilità di un satellite spaziale.

(1) Descrizione elementare del moto di precessione

Immaginiamo di prendere una bella trottola (per comodità, descriviamola come una sfera che gira intorno a un’asticella di legno che le passa da parte a parte, simile a un galleggiante per la canna da  pesca). La poggiamo su un tavolo e le  diamo un bel colpetto con la mano destra (molto deciso e senza far ballare la mano da un lato e dall’altro). Che meraviglia! Peccato che i bambini di oggi  la usino così poco. Se è colorata sembra un vero arcobaleno rotante.

Per qualche secondo (la durata dipende dalla velocità che le è stata impartita) la trottola mantiene una posizione perfettamente verticale. Addirittura, se cercate di sfiorarla, sentirete un vero colpo alla vostra mano, come se volesse cacciarvi via. Avete fatto conoscenza con il momento angolare della trottola, ossia con una grandezza fisica che regola la rotazione di un corpo attorno a un asse. Vi ricordate la pattinatrice su ghiaccio?

Se preferite, pensate a un pesante cancello di ferro che ruota attorno ai cardini. Non è certo facile interrompere il suo movimento e, se provate, ne sentite tutta la forza che ve lo vieta. E più il cancello è pesante e più è difficile bloccare la sua rotazione. Che cos’è, allora, il momento angolare? Si può definire come la capacità di un corpo di mantenere il suo  stato di rotazione. Oltretutto, dovreste anche sapere benissimo che se niente lo disturba o lo cambia esso si mantiene costante. Un vero e proprio signore della rotazione. Senza bisogno di scrivere formule, basta dire che la sua grandezza è data dal prodotto tra la velocità di rotazione e qualcosa (momento d’inerzia) che dipende dalla massa dell’oggetto che ruota e dalla sua forma. Con questa definizione si capisce benissimo che più il corpo è pesante, e/o più velocemente ruota, tanto più il momento angolare diventa potente e resistente alle provocazioni esterne.

Vi prego, però, di non confondere momento angolare con rotazione dell'oggetto. Se cresce il momento angolare non vuol dire che cresca anche la velocità di rotazione. Dovendo rimanere costante, se aumento la massa o le sue dimensioni rispetto al punto di rotazione, sono costretto a diminuire la velocità. Chi ogni tanto guarda il cielo notturno e le sue meraviglie, fermandosi quando è possibile su Giove, si ricordi che la grande macchia rossa del gigante è un ciclone in rapida rotazione, il cui momento angolare si mantiene inalterato da secoli, proprio perché non è  assolutamente facile annullarlo. Esattamente come cercare di fermare un cancello enorme. Per annullarlo ci vogliono "forze" esterne e non è facile trovarne di così potenti. Chi osserva Giove si ricordi anche di questo... e la macchia rossa sarà ancora più bella!

Avete sicuramente già capito che se il tavolo fosse perfetto, ossia se non ci fosse attrito tra lui e la trottola, e se voi foste stati perfetti nel dare il colpo iniziale, la trottola continuerebbe per sempre a ruotare, mantenendo costante il suo momento angolare, ossia la sua capacità di ruotare. La situazione sarebbe quella descritta in Fig. 1. Si può notare una configurazione importantissima per l’equilibrio perfetto: la forza di gravità della trottola, applicata al suo centro di gravità G, passa esattamente per il punto di contatto con il tavolo, ossia è perfettamente verticale. A sinistravi è una visione della trottola vista dall'alto; a destra essa è vista sul piano perpendicolare, rappresentato dalla linea verde PQ.

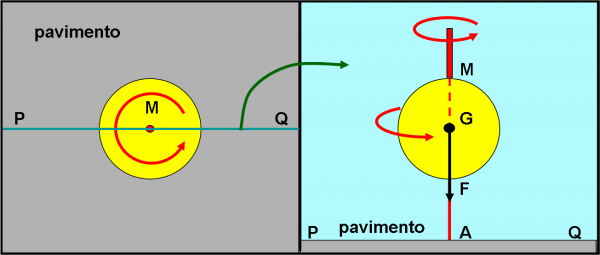
Purtroppo, queste sono condizioni ideali che prima o poi non riescono più a mantenersi. La punta della trottola “raschia” sul tavolo e fa rallentare la rotazione (il momento angolare cambia perché l’attrito è una forze esterna) e prima o poi capita un qualcosa che dà inizio alla fine del gioco. Questo qualcosa è il semplice fatto che l’asse di rotazione inizia a non essere più perfettamente verticale.  Vediamo questa situazione nella Fig. 2.

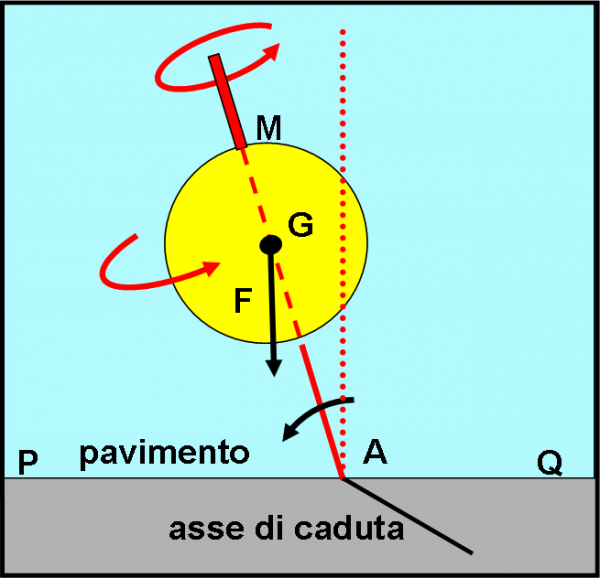
Non appena l’asse di rotazione perde la sua verticalità, ecco che la forza di gravità (applicata al  baricentro G) non passa più per il punto d’appoggio. La trottola tende, allora, a ruotare (cadere) verso il basso per effetto di ciò che viene chiamato momento di una forza (in questo caso quella di gravità). In parole povere, la forza tende a imprimere una rotazione alla trottola attorno a un asse che è quello che ho chiamato “asse di caduta” e che è perpendicolare al piano del disegno (un momento è diretto nella direzione perpendicolare al piano in cui avviene la rotazione).

Questo momento è quello che tende a far cadere la trottola verso il tavolo. Anzi, se la trottola non ruotasse per niente, la farebbe cadere immediatamente. Tuttavia, dato che la trottola continua a ruotare attorno al suo asse, questo momento che cerca di farla cadere si somma a quello che la tiene in rotazione (il momento angolare iniziale). In parole più semplici, alla rotazione normale si aggiunge un movimento di caduta verso il tavolo che sposta istante per istante l’asse della trottola e la obbliga a percorrere una traiettoria circolare attorno alla verticale che passa per A (l’originale asse di rotazione). In altre parole, la trottola tenderebbe a cadere verso il basso, ma la sua rotazione la riporta un po' verso l'alto e lei continua a girare intorno a un asse che descrive un cono attorno all'asse di rotazione originario.  Questo movimento è proprio il moto di precessione della trottola. Lo possiamo vedere nella Fig. 3 .

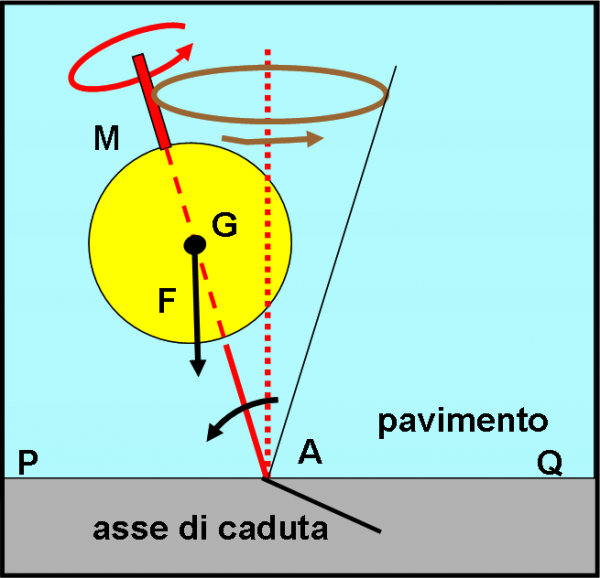
Purtroppo, l'attrito sul pavimento fa rallentare la trottola e più lei rallenta è più il momento della forza di gravità la spinge verso il pavimento, allargando il cono di precessione. Alla fine cade e tutto finisce.

(2) Descrizione semi-tecnica del moto di precessione

Nella trattazione precedente abbiamo appena accennato ai “signori” della rotazione, ossia ai momenti angolari. Ci sono solo serviti per introdurre rotazioni evidenti attorno a due assi, quello di rotazione e quello di caduta. Non abbiamo, però,  calcolato  come essi si combinano per dar luogo al moto di precessione. Lo abbiamo dovuto accettare come un dato di fatto.  Pur mantenendoci a livello elementare, vediamo allora di capire meglio perché il movimento finale è proprio lungo quello strano cono.

Consideriamo la Fig. 4, che non differisce di molto dalla Fig. 2, a parte il fatto che abbiamo dato un nome e cognome al momento angolare L della trottola attorno al suo asse e al momento T (di caduta) che la fa ruotare verso il basso e che dipende dalla forza di gravità. Entrambi sono dei vettori, ossia sono definiti da un valore numerico, da una direzione e da un verso. Qualcosa di simile alle forze, che vengono indicate con una freccia di una certa lunghezza, direzione e verso.

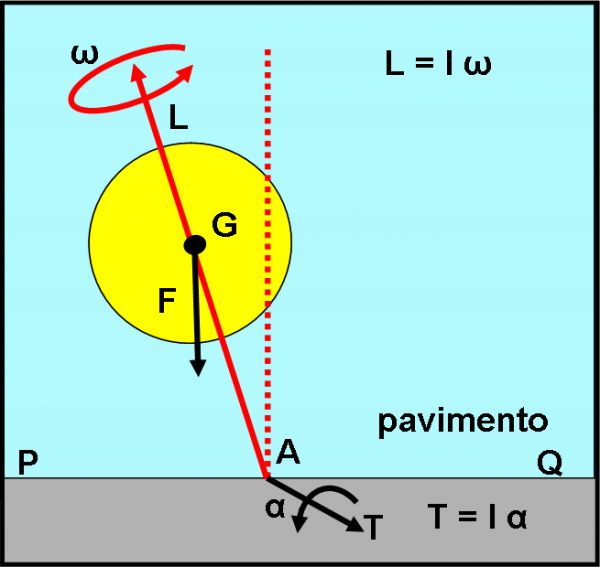
Se sono vettori, possiamo benissimo cercare di sommarli assieme secondo la regola del parallelogramma e trovare il vettore risultante. Attenzione: sto commettendo un errore di fisica abbastanza grave . Sto sommando un vettore che è un momento di una forza con un vettore che è un momento angolare. Tuttavia, a questo livello, posso permettermelo... (per essere più chiaro, ω è una velocità angolare, mentre α è un'accelerazione angolare, dato che la forza F, di gravità, impone un'accelerazione alla caduta verso il basso). Andiamo, comunque, avanti, riflettendo ancora una volta che senza la matematica si è costretti a commettere errori più o meno importanti.

Disegniamo  la Fig. 5 e vediamo di spiegarla con precisione. In un certo istante i vettori che agiscono sulla trottola sono L  e T rossi. Essi sono uno perpendicolare all'altro per definizione e stanno su uno stesso piano. Posso sommarli e trovare il vettore risultante che sarà il nuovo asse di rotazione della trottola (L', colorato in blu). Tuttavia, se si il vettore L si è spostato in L', deve essersi mosso anche il vettore T che per definizione deve essere perpendicolare a L' in ogni istante. Esso diventerà, quindi, quello blu (T'). Posso, adesso, lavorare nel piano di L' e T' e calcolare il nuovo vettore somma. Esso sarà L"  (arancione). Ma L'' arancione implica un nuovo T'', anch'esso arancione, a lui perpendicolare. In questo nuovo piano si ottiene il vettore risultante L''' (verde). Non c'è bisogno di andare avanti. Il procedimento l'avete capito. Ciò che si vede è che l'asse di rotazione L si sposta in L', L'', L''', ecc., ossia descrive proprio un cono attorno all'asse di rotazione iniziale. Non cambia il suo valore numerico, ma cambia la sua direzione.

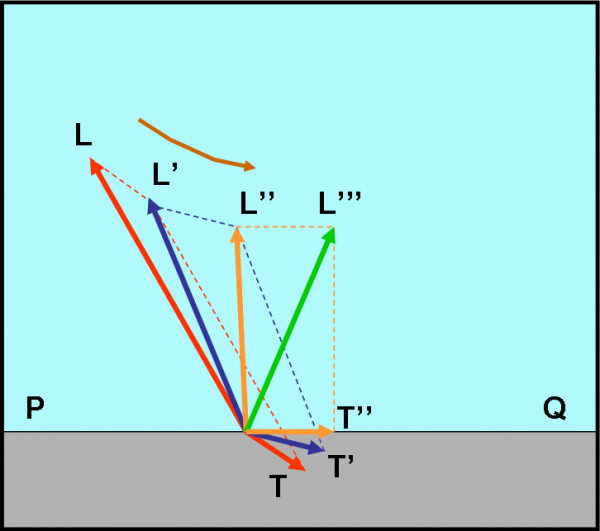
Voglio ripetere ancora una volta che il metodo descrittivo  usato sopra non è né carne né pesce e implica anche qualche errore fisico. Non riesce nemmeno a quantificare il valore numerico della precessione. Ha il solo vantaggio di cercare di far comprendere in modo empirico perché l'asse si muove e perché si muove in un certo modo. Tutto lì... Consideratelo per quello che è e non pretendete troppo da lui.

(3) Descrizione tecnica del moto di precessione (ma non poi troppo)

Sappiamo già che la trottola ruota attorno al suo asse con velocità angolare ω e che il suo momento angolare è dato da L  = Iω, dove I è il momento d’inerzia della trottola (grandezza che dipende dalla massa e dalla forma del corpo). Il momento angolare L è diretto lungo l’asse di rotazione. Introduciamo la Fig. 6 (sempre la stessa, ma un po' più seria e con i valori matematici espressi compiutamente).

Se la forza di gravità F = mg non è diretta verso A, si crea un momento della forza F che è diretto perpendicolarmente al piano di rotazione, ossia lungo l’asse di caduta. Esso vale T = F r', ossia è dato dalla moltiplicazione della forza per la distanza dall'asse originario di L . Per essere esatti dovrei dire che T è dato dal prodotto vettoriale dei due vettori F e r'. Il prodotto vettoriale è un vettore che è perpendicolare al piano individuato dalla forza e dal suo spostamento, ossia è proprio diretto lungo la direzione di T. Siamo costretti a prenderlo per buono, dato che dovremmo lanciarci all'interno di una fisica che non abbiamo mai trattato. Tuttavia, il valore numerico di T (il suo modulo) può essere calcolato dalla geometria della forza in gioco (F) e dalla sua distanza dalla verticale (r'), come indicato in Fig. 6:

T = F r' = mg r sinФ

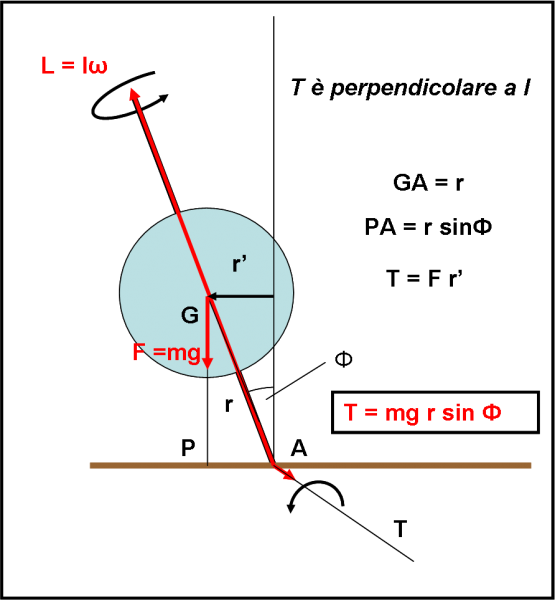
A questo punto abbiamo due momenti, due signori della rotazione, che sono uno perpendicolare all’altro. Il momento angolare L di rotazione agisce lungo l’asse della trottola, ma il momento della forza F (T) è perpendicolare ad esso.  Dalla fisica si sa che lo spostamento di un momento angolare (L) che subisce un momento di una forza (T) avviene in modo perpendicolare a L. E' la stessa cosa che capita per la velocità di un punto che ruota a distanza r dal centro di una circonferenza. Essa è sempre perpendicolare al raggio r . In altre parole, lo spostamento di L avviene proprio nella direzione di T. E' anche possibile dire che la variazione della posizione di L rispetto al tempo non è altro che il vettore T (è proprio lui che la causa).  In altre parole, l'asse di rotazione descrive l'arco ΔL e la sua variazione rispetto al tempo è proprio uguale al momento T. 

T = ΔL /Δt

La Fig. 7 mostra la situazione.

E’ proprio questo movimento che viene chiamato precessione. Tuttavia, adesso siamo in grado di calcolarlo. Possiamo, infatti, scrivere, come calcolato  precedentemente, che T =  mg r sinФ

Eguagliando le due ultime relazioni si ha:

mg r sinФ = ΔL/Δt

La Fig. 7 ci dice, però,  anche come legare il valore di ΔL al momento L (il suo valore numerico non cambia, cambia solo la direzione). Un legame che non è proprio esatto, ma la differenza è trascurabile in quanto abbiamo soltanto sostituito il seno o la tangente di un angolo molto piccolo con l’angolo stesso:

ΔΘ ~ ΔL/(L sin Ф)

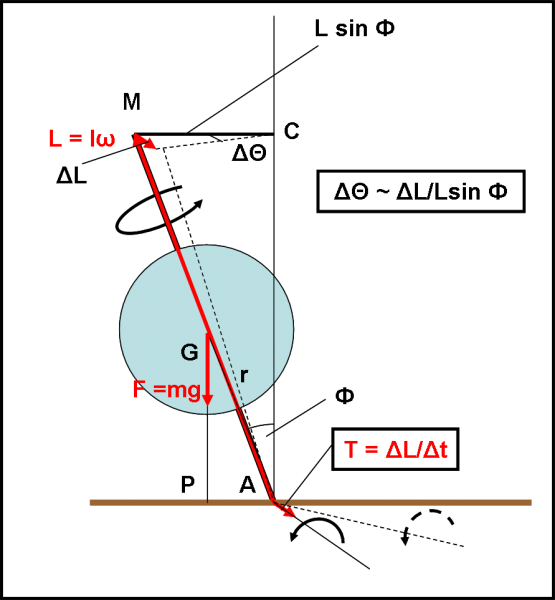
A questo punto non ci rimane che fare qualche sostituzione nelle formule che abbiamo scritto precedentemente, tenendo presente che la velocità angolare del moto di precessione può definirsi come

ω_P = ΔΘ/Δt

dato che è proprio la variazione dell’angolo Θ in funzione del tempo.

ω_P = ΔΘ/Δt = ΔL/(Δt L sin Ф) = mgr sinФ/(L sin Ф) = mgr/L = mgr/Iω

ossia:

ω_P = mgr/Iω

Questa relazione ci dimostra che il moto di precessione dipende dalla massa della trottola, ma anche dalla velocità di rotazione. Se essa è molto rapida la precessione è molto lenta. Questo è verificabile direttamente giocando con la trottola: provare per credere. La situazione finale è riportata nella Fig. 8.

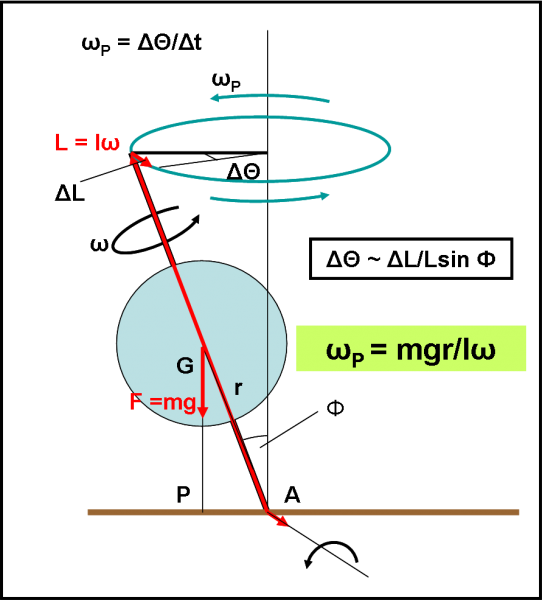
Cosa dirvi? Beh… con questa trattazione siamo riusciti a descrivere quantitativamente la precessione. Tuttavia, non siamo comunque riusciti a spiegare ogni singolo passaggio. I prodotti vettoriali e  le derivate non sono ancora nel bagaglio di tutti e ho preferito non andare troppo in là. Una via di mezzo, un compromesso. Posso, però, assicurarvi che la soluzione del moto di precessione è tutt’altro che banale (forse ve ne siete accorti). Sia come sia, la formula l’abbiamo ricavata e chi si vuole divertire, può applicarla a tutte le trottole che vuole.

La nutazione in poche parole

Chi ha seguito la terza parte della precessione si sarà reso conto del perché preferisco evitare del tutto una trattazione matematica della nutazione. Essa, in poche parole, ci dice che la situazione descritta precedentemente (che già è abbastanza complicata) peggiora ancora. Non esiste più solo un moto di rotazione attorno all’asse e un moto di caduta verso il tavolo, ma anche il nuovo moto di precessione. Devo quindi tenere conto anche di quest'ultimo. Cosa implica tutto ciò? Che la trottola oscilla avvicinandosi e allontanandosi dall’asse verticale durante il suo moto di precessione (fidatevi!). Questa oscillazione, di periodo piuttosto breve, prende il nome di nutazione ed è quindi una diretta conseguenza della precessione.

In generale, però, si usa (sbagliando) definire come nutazione  qualsiasi oscillazione dovuta a perturbazioni esterne. Ad esempio, nel caso della Terra, quella dovuta ai pianeti e a volte anche a quella della Luna (che invece va considerata assieme al Sole per definire la forza F che fa "cadere" la trottola). Queste però sono solo perturbazioni alla teoria classica della precessione, che -ripeto-  implica già, automaticamente e da sola,  la nutazione.

Anche la Terra è una trottola

Eh sì, anche la Terra è sicuramente una trottola che ruota attorno a un asse di rotazione (basta guardare la polare e le altre stelle, durante qualche ora, per farcelo venire in mente). Qualcuno potrebbe dirmi: “Sì, ruota, ma per lei non esiste un tavolo su cui è poggiata, una verticale e nemmeno una forza di gravità che la fa cadere. Dovrebbe quindi girare senza alcun problema”.

Purtroppo no. Basta vedere le cose in un contesto più generale e non soltanto legato alla trottola Terra. Iniziamo, semplificando la faccenda ed escludendo la Luna (ogni tanto dà un po’ di fastidio). La parte del “tavolo” è fatta dall’orbita della Terra attorno al Sole; la verticale è la perpendicolare a questo tavolo, ossia la perpendicolare al piano dell’eclittica. Non basta ancora, però, per far diventare il nostro pianeta una vera e propria trottola con i suoi strani movimenti.

La rotazione della trottola Terra fa sì che essa si schiacci ai poli e si “allarghi” all’equatore. In altre parole, la sfera diventa un ellissoide, come quello rappresentato in Fig. 9. “Poco male”, potremmo dire, "la trottola, pur se deformata, mantiene una simmetria rispetto all’asse di rotazione. D’altra parte, sappiamo bene che la forma delle trottole giocattolo hanno spesso forme molto strane eppure funzionano lo stesso. Il momento angolare della trottola, diretto lungo l’asse di rotazione, coincide ancora perfettamente con la verticale del piano del tavolo (piano Terra-Sole)".

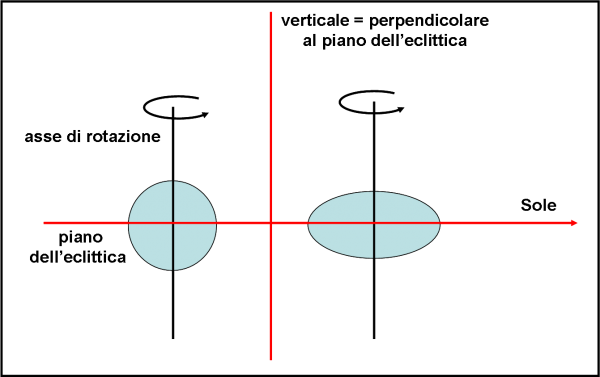
Ne siamo proprio sicuri? No, purtroppo no. La Terra ha il grave difetto di girare attorno a un asse che non è perpendicolare alla verticale. Anzi, lo fa con un angolo di circa 23 gradi, proprio quello che separa il piano dell’eclittica dal piano equatoriale della Terra, ossia quello perpendicolare all’asse di rotazione. La situazione è allora quella di Fig.  10.

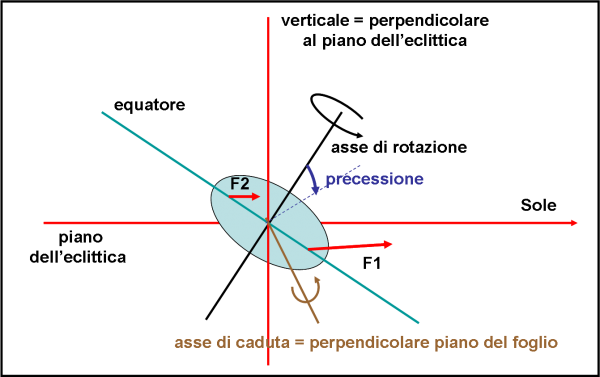
La parte allungata della Terra della parte destra viene attirata di più dal Sole rispetto a quella sinistra (proprio come capita nella marea) e questa "coppia" di forze (che sono sempre la gravità) tende a far ruotare il pianeta attorno a un asse che ho ancora chiamato asse di caduta (la retta marrone diretta verso il lettore e che è perpendicolare al foglio del disegno). E’ stato introdotto un nuovo momento che tende a far cadere la trottola verso la verticale (invece che verso il tavolo; ma è la stessa identica cosa, dato che è comunque una rotazione ). La situazione è allora perfettamente identica a quella che avevamo descritto per la trottola: l’asse di rotazione della Terra inizia a muoversi attorno all’asse dell’eclittica di moto circolare, ossia seguendo il moto di precessione. Insieme alla precessione sorgerà anche la nutazione come ovvia conseguenza.

Le cose per noi, però, sono un po’ più complicate, dato che (come per la marea) esiste anche la Luna, piccola ma vicina. Oltretutto, la argentea signora della notte ha la brutta abitudine di girarci intorno su un piano che non è né quello del nostro equatore né quello dell’eclittica. Ne consegue un moto di precessione molto più complicato e così anche quello di nutazione. Diciamo meglio: il moto alla fine avverrà sempre, in prima approssimazione, attorno all’asse dell’eclittica, ma il tempo necessario a descriverlo sarà diverso e la traiettoria piena di ondulazioni abbastanza anomale, benché decisamente molto piccole.

In ogni modo vi è un grande vantaggio rispetto alla trottola sul tavolo. Non ci sono attriti e la rotazione attorno all’asse di rotazione resta sempre uguale. Conclusione? La trottola non “cadrà”, ossia il suo asse non coinciderà mai con quello dell’eclittica. In realtà non è proprio vero, perché la Luna fa di tutto per farci rallentare, ma la quantità è così piccola che possiamo tranquillamente trascurarla. Così come possiamo trascurare l’aiuto nella “caduta” (anche in verso opposto) dovuto ai pianeti del Sistema Solare. Sono tutti desiderosi di spostare il nostro povero asse di rotazione!

Ho trovato una bella figura su Wikipedia (Fig. 11) per mostrare in 3D la precessione e tutte le rotazioni che la causano. Dopo la nostra lunga trattazione possiamo anche utilizzarla e spiegarla un po’ meglio. Teniamo conto che in questa figura la dilatazione della zona equatoriale è stata rappresentata come un anello aggiuntivo posto all’equatore terrestre. Poco importa, il succo è lo stesso.

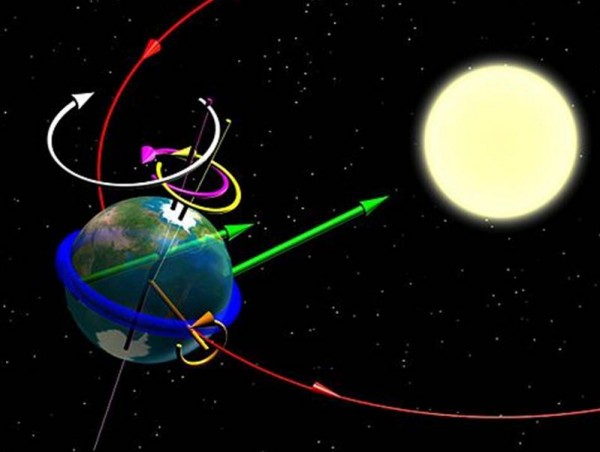
Le frecce verdi  indicano la coppia di forze che causano la “caduta” verso l’asse dell’eclittica e quindi causano la rotazione rappresentata in arancione. L’asse di questa rotazione (il momento della forza) è perpendicolare all’asse di rotazione della Terra attorno al proprio asse. Questa rotazione fondamentale è rappresentata in viola. Tuttavia, sappiamo che il momento della rotazione arancione trascina verso di sé il momento della rotazione viola, obbligando quest’ultimo a spostarsi e a produrre la rotazione gialla. L’insieme delle nuove posizioni assunte dall’asse di rotazione descrive il cono attorno all’asse dell’eclittica, ossia segue la rotazione bianca. Quest’ultima è proprio il moto di precessione. Direi che non è il casso di inserire anche la nutazione nella stessa figura (poveri noi!). Ci basti rappresentarla schematicamente come indicato nella Fig.12, anch’essa tratta da Wikipedia.

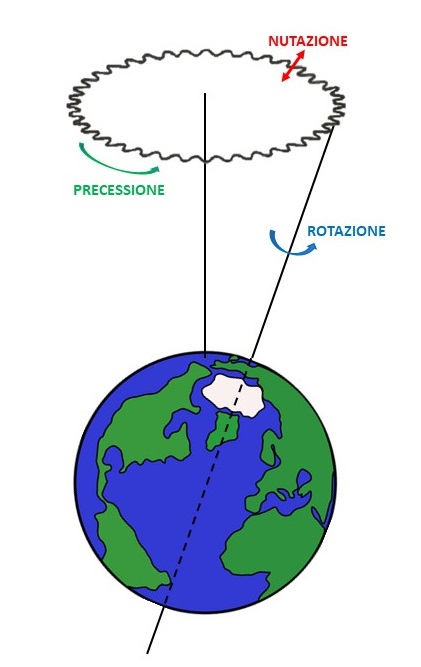
Vale la pena dare risalto a un fatto che non sarà sfuggito ai più attenti e/o esperti: il moto di precessione della Terra è orario mentre quello di rotazione su se stessa è antiorario. Tutto ciò sembra in contrasto  con l'esempio della trottola. No, tutto dipende dalla forza che fa “cadere” la trottola e la Terra. Nel primo caso essa tende a farla allontanare dalla verticale; nel caso della Terra, la forza tende, invece, a farla avvicinare alla verticale, ossia all’asse dell’eclittica. E' sempre questione di verso del momento di una forza.

Potremmo dire che in Natura tutto precede, dato che ben poco avviene in modo perfetto. Precedono le pulsar, ma precedono anche le orbite dei pianeti e delle stelle (QUI la precessione, osservata in diretta, dell'orbita di una stella intorno al nostro buco nero galattico) e sicuramente anche le galassie. Fortunatamente, i moti di precessione non sono caotici, in prima approssimazione, e possono essere trattati analiticamente.

Nel caso dell’asse di rotazione della Terra si riesce a farlo abbastanza bene, anche tenendo conto dei pianeti. Purtroppo, il nostro asse di rotazione ha, però, altri movimenti che dipendono dalla variazione della distribuzione interna delle masse. Ne segue che il polo istantaneo di rotazione viaggia in modo bizzarro attorno a un valore medio. Questo movimento, fortunatamente molto piccolo, può solo essere osservato direttamente e non previsto in anticipo. Si chiama polodia.

In realtà, esso differisce dai moti precessionali, in quanto in quest’ultimo caso è tutta la Terra che si muove insieme al suo asse, mentre nella polodia è solo l’asse che si muove rispetto alla Terra. Va beh… basta, non complichiamo ancora di più la faccenda.

Conclusioni 

Questo articolo è (in certe parti) sicuramente difficile e nemmeno spiegato completamente. Una ragione per pubblicarlo, comunque c'è. Quella di mostrare quanto varino le cose a mano a mano che si procede (non PRECEDE!) verso una descrizione rigorosa. Questo fatto implica una riflessione. Coloro che, limitandosi a una visione empirica e facilitata dei fenomeni celesti, concludono che nella scienza è tutto ancora troppo aleatorio, commettono un errore di superbia. Dato che sanno poco, automaticamente trasferiscono questa loro limitazione (del tutto plausibile e giustificata) anche alla Scienza con la S maiuscola. La divulgazione, purtroppo, deve limitarsi a uno stadio elementare e non può certo descrivere tutti i calcoli e i modelli che stanno dietro a certe conclusioni. La precessione è un esempio perfetto. Oltretutto, la difficoltà che abbiamo riscontrato nel terzo metodo è ancora mostruosamente semplice. Esso, infatti, non considera tutte quelle perturbazioni  a cui ho accennato. Eppure, ogni singola perturbazione è descrivibile con formule esatte e la soluzione si può ottenere senza grossi problemi. La meccanica celeste è veramente a un livello mostruosamente accurato, non dimentichiamolo mai. E, nemmeno, diciamo che deve per forza essere sbagliata perché si basa sulla legge di Newton. Sappiamo benissimo che lavorando nel Sistema Solare può anche bastare. Tuttavia,  ormai i conti di meccanica celeste di alto livello tengono in conto le influenze della Relatività. Diamo alla Scienza quello che è della Scienza. Scusatemi per questa "paternale", che vuole solo essere uno stimolo per aiutare a comprendere che la Scienza del Cosmo non si può valutare solo attraverso le notizie fornite a un pubblico "normale"  di non addetti ai lavori...

Finisco con una riflessione abbastanza frustrante per chi guarda il cielo anche con mezzi ben più sofisticati di quelli che avevano a disposizione i grandi scienziati antichi. Ipparco aveva già dato una descrizione illuminante della precessione (vedi QUI), ma si dice che fosse già conosciuta sia dai babilonesi che dagli egiziani. Oggi, sembrerebbe davvero incredibile. Insomma, c'è modo e modo di osservare il cielo. Non bastano gli occhi, però. Ci vuole molta mente... e questa è una fatica che non tutti possono o vogliono fare.