La soluzione è decisamente più semplice di quello che poteva apparire alla prima occhiata. Basta far ruotare un triangolo e il gioco è fatto.

Come sempre il quiz è stato risolto dai nostri lettori, ma diamone comunque una soluzione semplicissima. La risposta è facile: il perimetro del triangolo EFB non cambia al variare di di E di F, sempre che l'angolo EDF rimanga di 45°, e il risultato è 2, il doppio del lato, ossia il perimetro è la metà di quello del quadrato iniziale (interessante, non è vero?).

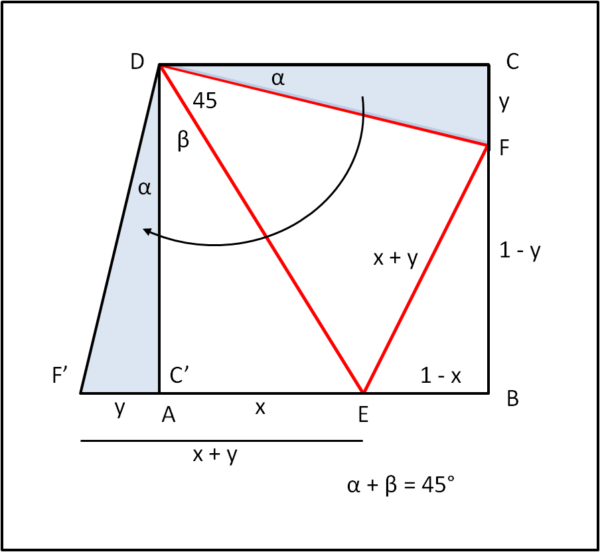
Il tutto è riassunto nella figura che segue.

Basta tener conto che gli angoli di un quadrato valgono 90° e  quindi α + β deve essere di 45°. Basta ora ruotare il triangolo FDC  intorno a D, fino a che DC coincida con DA.  Il triangolo DF'C' è, perciò, uguale a DFC. Il triangolo F'DE deve essere uguale al triangolo FDE, in quanto DF= DF' per costruzione, DE è in comune e l'angolo F'DE = FDE = 45°.

Chiamiamo AE = C'E = x e CF = C'F' = y. Ne segue che il lato F'E = x + y. Ma, essendo uguali i due triangoli, segue anche che EF = EF' = x + y. I lati del triangolo che ci interessa sono, perciò:

FB = 1 - y

EB = 1 - x

FE = x + y

Sommiamoli e troviamo il perimetro:

FB + EB + FE = (1 - y) + (1 - x) + (x + y) = 2

Come già anticipato, il perimetro non dipende dai punti E e F, ma è una costante uguale alla metà del perimetro del quadrato di partenza. L'importante è che l'angolo EDF sia sempre di 45°.

Bravi, come sempre, Andy e Arturo!

Il quiz lo trovate QUI