A proposito di quintiche... ***

02/08/20

A proposito di quintiche... ***

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:7

Per chi ha risolto una quintica, questa nuova domanda non dovrebbe porre problemi. Di certo farà una scorpacciata "algebrica".

Sappiamo che:

a + b + c = 1

a2 + b2 + c2 = 2

a3 + b3 + c3 = 3

Quanto vale la relazione seguente:

a5 + b5 + c5 = ???

Se il gioco vi è piaciuto potete sempre provare anche con:

a6 + b6 + c6 = ???

Un bel passatempo...

La soluzione la trovate nei commenti (grazie Andy) e anche QUI

Articoli correlati

7 commenti

  1. Andy
    03/08/2020 at 16:20

    Spero di non incartarmi:

    dato che: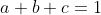  a+b+c=1

    si può scrivere la relazione di 2° grado come:

    \frac{a^2+b^2+c^2}{a+b+c}=2(a+b+c)    che equivale a   a^2+b^2+c^2=2(a+b+c)^2

    e sviluppando il quadrato del trinomio: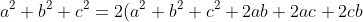  a^2+b^2+c^2=2(a^2+b^2+c^2+2ab+2ac+2cb)

    ovvero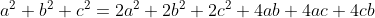 a^2+b^2+c^2=2a^2+2b^2+2c^2+4ab+4ac+4cb  e semplificando

    a^2+b^2+c^2=-4(ab+ac+cb)    =>   ab+ac+cb=-\frac{a^2+b^2+c^2}{4}

     

    Come fatto in precedenza, la relazione di 3° grado si può scrivere

    \frac{a^3+b^3+c^3}{a+b+c}=3(a+b+c)      cioè    a^3+b^3+c^3=3(a+b+c)^2

    ovvero   a^3+b^3+c^3=3[a^2+b^2+c^2+2(ab+ac+bc)]

    che equivale a  a^3+b^3+c^3=3 \left (a^2+b^2+c^2-2\cdot\frac{a^2+b^2+c^2}{4} \right)

    ovvero  a^3+b^3+c^3=3\left [ \frac{1}{2}\cdot (a^2+b^2+c^2) \right ]     <=>    a^3+b^3+c^3=\frac{3}{2}\left ( a^2+b^2+c^2 \right )

     

    Ricapitolando abbiamo:

    a+b+c=1

    a^2+b^2+c^2=\frac{2}{1}\left ( a+b+c \right )

    a^3+b^3+c^3=\frac{3}{2}\left ( a^2+b^2+c^2 \right )

     

    dovrebbe essere allora:

    a^4+b^4+c^4=\frac{4}{3}(a^3+b^3+c^3)=\frac{4}{3}\cdot\frac{3}{2}\cdot2(a+b+c)

    a^5+b^5+c^5=\frac{5}{4}(a^4+b^4+c^4)=\frac{5}{4}\cdot\frac{4}{3}\cdot\frac{3}{2}\cdot\frac{2}{1}(a+b+c)

    a^6+b^6+c^6=\frac{6}{5}(a^5+b^5+c^5) =\frac{6}{5}\cdot\frac{5}{4}\cdot\frac{4}{3}\cdot\frac{2}{1}\cdot(a+b+c)

     

    Anche se rimango dubbioso :roll:

     

  2. Vincenzo Zappalà
    03/08/2020 at 17:17

    Caro Andy,

    come sempre sei molto astuto, ma questa volta la tua formula ricorrente non funziona... Te lo posso dimostrare facilmente:

    Se a4 + b4 + c4 = 4 dovrebbe anche essere a4 + b4 + c4 = 2·2 = (a2 + b2 + c2)(a2 + b2 + c2)

    Facciamo l'ultimo prodotto, il quadrato di un trinomio:

    a4 + b4 + c4 + 2a2b2 + 2 a2c2 + 2 b2c2

    esso dovrebbe essere uguale a a4 + b4 + c4 , ossia dovrebbe essere

    2a2b2 + 2 a2c2 + 2 b2c2  = 0

    Ma questo è possibile solo se almeno due termini (ad esempio a e b) fossero uguali a zero

    a + b + c = 1

    0 + 0 + c = 1

    vorrebbe dire che c  dovrebbe essere uguale a 1

    ma già la seconda espressione non andrebbe bene:

    0 + 0 + 1 ≠ 2

    e anche la terza

    0 + 0 + 1  ≠ 3

    La faccenda è un po' più complicata, anche se si può risolvere con la semplice algebra e... tanta pazienza.

    Può darsi, però, che ci sia un metodo migliore del mio! Forza, tu puoi riuscirci!

     

  3. Vincenzo Zappalà
    03/08/2020 at 17:30

    Un consiglio (almeno per il metodo che ho usato io): occupatevi SUBITO di a5 + b5 + c5 senza pensare ad a4 + b4 + c4...

    Una formula ricorrente c'è, ma , almeno per il momento, non pensiamoci... è di algebra superiore, mentre le due espressioni che vi ho proposto possono essere trovate con l'algebra più semplice.

    Se si trovano i trucchetti giusti, è al livello di uno studente delle superiori, non di più

  4. Andy
    04/08/2020 at 01:26

    Grazie del suggerimento Enzo,

    ho aggiustato la mira :mrgreen:

    Per la relazione di 6° grado tenterò quando sarò meno stanco, o ancora meglio se qualcun altro la risolva

  5. Vincenzo Zappalà
    04/08/2020 at 05:20

    caro Andy... lo sapevo che sei astuto (e molto preparato). Detto fra noi, una volta risolata per l'esponente 5, l'esponente 4 è semplice, da cui risulta velocemente anche il valore per l'esponente 6. In ogni modo l'esponente 6 può anche essere risolto per  primo. Come hai visto i trucchetti da usare sono diversi, ma il succo è sempre quello: basta un'algebra semplice, ma molta fantasia... Spero ti sia divertito! Grazie!! :lol:

  6. Andy
    04/08/2020 at 14:49

    Grazie a te Enzo che proponi anche, tra le tantissime altre informazioni, quiz sempre interessanti e istruttivi.

    Bene, allora come "si ' fatto 30 si fa 31";

    questi dovrebbero essere i valori associati alle relazioni di 4° e 6° grado:

  7. Vincenzo Zappalà
    04/08/2020 at 15:02

    Bravissimo Andy!

    Purtroppo in questo periodo sei il solo che affronta di petto e -soprattutto- risolve i quiz di un certo livello. Ti devo ringraziare di vero cuore. Aspettando che anche altri si inseriscano nel nostro faccia a faccia, io continuo a proporne... non si sa mai e poi se so che tu diverti, è già di per sé sufficiente a metterli sul blog :wink:

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.