Categorie: Matematica
Tags: bottiglie geometria piramide quiz scatola sistemazione
Scritto da: Vincenzo Zappalà
Commenti:4
Quasi-soluzione al problema delle bottiglie di vino **
Diamo soltanto una risposta "preliminare" al problema delle bottiglie di vino, lasciando ancora aperta la dimostrazione...
Nelle condizioni illustrate nel quiz, la risposta alle domande (1) e (2) è: il centro della bottiglia più in alto sarà SEMPRE lo stesso, ossia cadrà a metà della larghezza della scatola.
Non resta che dimostrarlo!
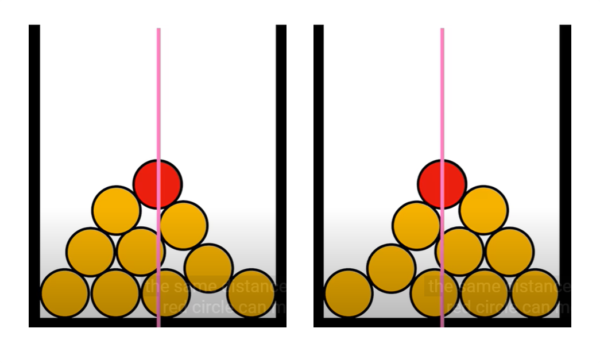
4 commenti
I centri delle bottiglie possono essere immaginati come vertici di una struttura a rombi. Linee rosse nella figura. Sono rombi perché hanno tutti i lati uguli a 2 volte il raggio delle bottiglie.
La posizione orizzontale di ciascun punto dipende dalle posizioni orizzontali dei vertici sottostanti.
Le posizioni orizzontali dei vertici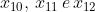
sono centrate rispetto ai vertici sottostanti, centri delle bottiglie alla base.
Per gli altri vertici la dipendenza è leggermente più complessa.
Ad esempio il vertice in cima (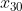
) è spostato leggermente a destra del punto intermedio dei due vertici sottostanti ( 
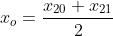). Lo spostamento è simmetrico a quello tra 
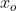ed il vertice sottostante 
.
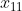Quindi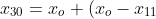=2x_o-x_{11}=x_{20}+x_{21}-x_{11})
Stesso ragionamento vale per le posizioni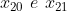
(vedi figura).
Sostituendo nelle espressioni delle posizioni dei centri di ciascun livello quelle trovate per i centri dei livelli inferiori si arriva ad ottenere che la posizione orizzontale del centro della bottiglia più in alto è centrata rispetto alle bottiglie alla base: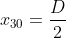
, dove D è la distanza tra i centri delle due bottiglie estreme alla base.
Le espressioni sono in figura.
caro Fabry... bravo come sempre, anche se non vi erano bisogno di formule, ma solo delle proprietà dei rombi.
Vediamo se riesci anche a trovare il significato del numero 7...
In effetti non servono le formule. Basta considerare che i lati opposti di un rombo sono paralleli e che i lati adiacenti hanno una inclinazione complementare a 180 gradi rispetto alla diagonale opposta. Allora tutti i lati esterni a sinistra hanno un lato con inclinazione complementare a destra. Il primo dei lati esterni a sinistra con l'ultimo destra, il secondo a sinistra con il punultimo a destra e così via. Poiché tutti i lati hanno la stessa lunghezza, le distanza dai due estremi della base non possono che essere uguali.
Questo permette anche di dire che vele per qualsiasi numero di bottiglie alla base
Il 7, potrebbe essere il numero di rombi. Ma forse è troppo semplice.
Un piccolo aiuto... la bottiglia da sola, in alto, rimane sempre ferma e quindi deve mantenere una simmetria perfetta... con cosa? Attenzione che il numero 7 vale per le 10 bottiglie soltanto e, oltretutto, ha dei limiti abbastanza precisi. Limiti che non ha la bottiglia in alto... Scusa, mi sa che confondo invece di aiutare... Ma ci arrivi sicuramente in quattro e quattr'otto!