Categorie: Matematica
Tags: geometria piega quiz semicerchio tangenza
Scritto da: Vincenzo Zappalà
Commenti:12
Pieghiamo un cerchio *
Vedo che il vino non piace molto (peccato...). Lasciamolo, comunque, in attesa di qualche estimatore. Nel frattempo, proponiamo questo quiz geometrico veramente semplice, a cui spero rispondano in tanti...
Prendiamo un foglio di carta e ritagliamo un bel semicerchio di raggio unitario, come mostrato in Fig. 1.

Poi pieghiamo la parte superiore e portiamola verso il basso in modo che essa vada a toccare in un solo punto T (ossia sia tangente) il diametro orizzontale, come mostrato in Fig. 2.
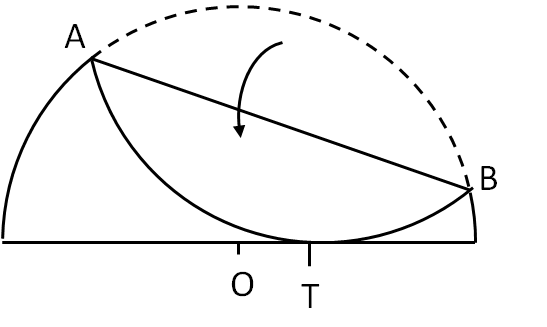
Si chiede:
(1) Quanto vale la distanza AB ?
(2) Qual è il suo valore minimo e massimo ?
(3) Che curva descrive la distanza AB al variare del punto T ?
La soluzione perfettamente spiegata la trovate nell'ultimo commento di Andy !






12 commenti
forse la soluzione del quesito è più evidente se la corda AB è posizionata parallelamente al diametro orizzontale del cerchio raffigurato in questo caso il punto di tangenza T coincide con il centro della circonferenza, in queste condizioni la saetta della corda AB e la sua distanza dal centro della circonferenza sono uguali ovvero valgono la metà del raggio:
indichiamo con h queste distanze uguali applicando il Teorema di Pitagora
(AB/2)2 = r2 - (r/2)2 = r2 - r2/4 = 3/4 r2
per r=1
(AB)2/4 = 3/4 AB = √3
OK Michele, ma è interessante vedere cosa succede nel caso generale e non solo in un caso molto particolare...
Se indichiamo con α l'angolo formato tra i i due raggi ed aventi per estremi A e B si ha:
sen α/2 = (AB/2) / r
da cui
(AB/2) = (sen α/2) r
AB = 2 (sen α/2) r
per r= 1
AB = 2 sen α/2
il valore minimo di AB è per sen α/2 = 0 ovvero per α = 0
il valore massimo di AB è per sen α/2 = (r/2) / r = 1/2
ovvero per α = 60 gradi, che corrisponde al caso particolare della corda parallela al diametro orizzontale di cui alla figura nel caso di saetta pari a metà del raggio.
La lunghezza della corda varia con legge sinusoidale con un minimo paria a 0 e un massimo pari
a √3
caro Michele,
ricordati bene le ipotesi di partenza: il cerchio piegato deve essere tangente al diametro orizzontale ... il valore minimo non è giusto.
E poi cerca di ricavare la funzione che esprime la lunghezza di AB in funzione della distanza del punto di tangenza rispetto al centro del semicerchio di partenza...
Aggiungo un tassello.
La lunghezza minima della corda AB si ha quando B coincide con uno degli estremi del diametro. In questa circostanza, essa forma un angolo di 45° con il diametro e la dua lunghezza, calcolata con Pitagora, vale radq(2) (essendo il raggio =1).
Non resta che ricavare la funzione per un caso qualsiasi...
Se non ho sbagliato i conti, la formula che restituisce la lunghezza della corda AB al variare di x (indicando con x la lunghezza del segmento OT) è :
Infatti:
Trovare la formula è quasi immediato, una volta fatta una corretta costruzione grafica del problema , che ometto per chi volesse arrivarci da solo
Oh, sempre la formula è giusta, eh
("sempre SE la formula è giusta")
e che curva sarebbe mai quella trovata? (aggiungo)
Un arco di circonferenza di raggio pari a radq(3)
In linea con quanto ha già scritto Arturo, nel caso generale:
bravissimi!!!