Questo articolo è stato inserito nella sezione d'archivio "Matematica e Geometria"

 

Un monte veramente matematico, la cui utilità è enorme e forse i misteri che racchiude non sono stati ancora tutti risolti. Non possiamo, perciò, stupirci se nell'antichità era considerato un monte sacro!

Un po' di storia

Non cercate su wikipedia il Monte Meru... ve lo daranno come vulcano attivo della Tanzania, alto 4556 metri. No, non ha niente a che vedere con il "nostro" monte anche se un vulcano ben si associa a una forma geometrica (cono). Il Monte Meru che ci interessa è una montagna sacra della mitologia induista e buddhista, considerato il centro del "Piccolo Universo".

Sulla sua cima sorge il Paradiso di Indra. Prima di andare avanti, riflettiamo un attimo su questa simbologia: montagna sacra alla cui cima inizia il Paradiso... non è difficile confrontare questa raffigurazione con quella della montagna del Purgatorio descritta da Dante nella sua Divina Commedia. Anch'essa è un monte perfetto che conduce al Paradiso. Che poi Dante abbia ideato un paradiso in quattro dimensioni è tutt'altra cosa.

Resta il fatto, però, che questa montagna così speciale viene abbastanza presto identificata come struttura "matematica". In particolare, si definisce una scala per raggiungerne la cima ed essa viene chiamata  Meru Prastaara già nel secondo secolo d.C. Sicuramente, la sua "costruzione" è definita con grande precisione dal matematico indiano  Varahamihira nel 505 d.C. e, ancora più accuratamente, da Halyudha nel 975 d.C.

Contemporaneamente un triangolo simile alla scala viene descritto anche in Persia da Al-Karaji e, poco più tardi, dal matematico e poeta Omar Khayyám (1048-1131). Ormai il monte Meru è diventato un vero e proprio triangolo ricco di misteri matematici più o meno svelati.

La Cina non è da meno e all'inizio dell'XI si ritrova la "scala" nel lavoro del matematico Jia Xian, ripreso nel 13° secolo da Yang Hui (1238-1298).

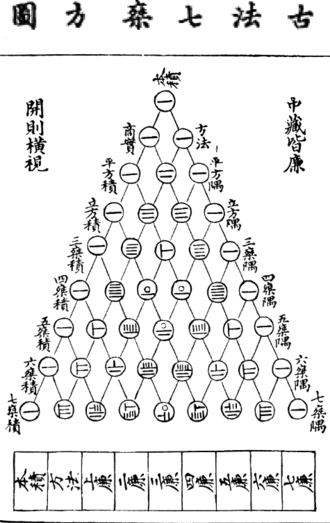
In Oriente, perciò, il triangolo passa ai posteri con il nome di triangolo di Khayyám e/o con quello di triangolo di Yang Hui (beh... un po' di campanilismo c'è sempre stato...).

In Europa, bisogna aspettare Petrus Apianus, all'inizio del '500, per vederlo comparire nel frontespizio di un libro, ma soprattutto Niccolò Tartaglia che lo illustra compiutamente pochi anni dopo. In Italia, perciò, è ora universalmente noto come triangolo di Tartaglia.

La storia non è ancora finita, però... nel 1655 il francese Blaise Pascal pubblica un trattato su questo triangolo, a cui viene  dato il nome di triangolo di Pascal.

Insomma, chiamatelo come preferite... a me piace ricordarlo come scala del Monte Meru, il monte più matematico che ci sia.

Costruiamo la scala

Vediamo ora di costruire questa straordinaria  "scala", in termini moderni ed estremamente semplici (evitiamo l'uso del binomio di Newton, di serie, di fattoriali e cose del genere... tanto il concetto rimane sempre lo stesso).

Costruiamolo in modo veramente banale:

Scriviamo una riga di zeri lunga a piacere. L'importante è che a un certo punto si inserisca il numero 1. Da questo punto in poi basta solo sapere fare l'operazione di somma...

Dedichiamoci soltanto ai "dintorni" del numero 1, considerando lo zero prima e lo zero dopo. Sommiamo 0 con 1 e poi 1 con 0. Il risultato lo scriviamo nella riga sotto tra i due numeri che abbiamo sommato, come mostra la Fig. 1.

Teoricamente, potremmo  sommare tra di loro anche le coppie di zeri e otterremmo un'altra serie, grande a piacere, di zeri che racchiudono i due 1 appena calcolati. ma non esageriamo e concentriamoci solo sui numeri diversi da zero (gli zeri l'immaginiamo soltanto).  Sapendo che da una parte e dall'altra di questi uno, anche se non rappresentato, vi è uno zero, ripetiamo il gioco di prima e scriviamo i risultato nella riga sottostante, sempre con le stesse modalità... 0 + 1 = 1, 1 + 1 = 2 , 1 + 0 = 1. Otteniamo la Fig. 2

La faccenda diventa sempre più interessante e possiamo ripeterla. Questa volta le somme che dobbiamo fare sono 0 + 1 = 1, 1 + 2 = 3, 2 + 1 = 3, 1 + 0 = 0 come mostra la Fig. 3.

Ormai la procedura è facile da ripetere, allargando sempre più il numero di numeri diversi da zero che compaiono nella riga sottostante. Ci accorgiamo che stiamo costruendo un triangolo di numeri interi, la cui base si allarga sempre di più. Un triangolo che termina sempre, sia a destra che a sinistra, con il numero 1 (0 + 1 = 1 e 1 + 0 = 1). Bene , possiamo proseguire quanto vogliamo: dato che i numeri interi sono infiniti, sarà anche infinito il numero di righe che si possono costruire. In qualche modo abbiamo costruito un "monte" numerico, perfettamente simmetrico senza una vera base, dato che questa può allargarsi sempre di più (Fig. 4)

Il primo, più diretto, utilizzo del nostro monte numerico, è legato ai coefficienti binomiali, ossia, in parole molto più povere, ai coefficienti di tutti i termini dello sviluppo delle potenze del binomio (a + b).

Tocchiamo subito con mano questa straordinaria capacità:

proviamo con (a + b) elevato a zero. Poco importa cosa valgano a e b, ma qualsiasi numero intero elevato a zero vale 1. In effetti, la cima del monte vale proprio 1.

(a + b)⁰ = 1

Passiamo a:

(a + b)¹ = a + b

Quali e quanti sono i coefficienti dei termini dello sviluppo della potenza uno del binomio? Beh... 1 e 1 (1a + 1b)

La seconda riga del monte, a partire dalla cima, ci dà proprio 1 e 1.

Passiamo a cose "più serie":

(a + b)² = 1 a² + 2 ab + 1 b²

Quali sono i coefficienti dei 3 termini? 1, 2 e 1, proprio la terza riga del monte.

Proviamo ancora con il cubo...

(a + b)³ = a³ + 3a²b + 3ab² + b³

I coefficienti sono proprio 1, 3, 3 e 1.

Bisognerebbe passare alla quarta potenza. Non esiste, in realtà, una formula mnemonica per potenze maggiori di 3. Possiamo, però, calcolare il risultato moltiplicando (a + b)³ per (a + b)

(a + b)⁴ =( a + b)³ (a + b) = (a³ + 3a²b + 3 ab² + b³)(a + b) = a⁴ + 3a³b + 3a²b² + ab³ + a³b + 3a²b² + 3 ab³ + b⁴

(a + b)⁴ = a⁴ + 4 a³b + 6 a²b² + 4ab³ + b⁴

I coefficienti sono 1, 4, 6, 4, 1, ancora una volta proprio la riga corrispondente del nostro magico monte.

Andare avanti comincia a essere abbastanza complicato, ma non certo guardando la struttura del monte: la riga sotto è, infatti, 1, 5, 10, 10, 5, 1 che, ormai lo sappiamo, sono i coefficienti dello sviluppo della quinta potenza del binomio.

Grazie alla scala del Monte Meru, possiamo scrivere immediatamente:

(a + b)⁵ = a⁵ + 5 a⁴b + 10 a³b² + 10 a²b³ + 5 ab⁴ + b⁵

Vogliamo provare ancora una volta in modo brutale, conoscendo già il risultato della quarta potenza?

(a + b)⁵ = (a + b)⁴ (a + b) = (a⁴ + 4 a³b + 6 a²b² + 4ab³ + b⁴)(a + b)

(a + b)⁵ = a⁵ + 4 a⁴b + 6 a³ b² + 4 a²b³ + ab⁴ + b⁵ + a⁴b + 4a³b² + 6a²b³ + 4ab⁴ + b⁵

(a + b)⁵ = a⁵ + 5 a⁴b + 10 a³ b² + 10 a²b³ + 5ab⁴ + b⁵

Direi proprio che il monte Muri diventa sempre più utile... immaginate, infatti, di scrivere la potenza quattordicesima di (a + b). Non è sicuramente qualcosa di impossibile, ma vi sfido a non commettere qualche piccolo o grande errore di scrittura. Con il monte-triangolo avete subito i coefficienti e basta "inserire" per ogni coefficiente le potenze di a per quelle di b, dove la somma degli esponenti sia sempre uguale alla potenza del binomio. Ad esempio se la potenza è la quinta, dobbiamo avere i termini a⁵, a⁴b, a³b², a²b³, ab⁴, b⁵  (nel giusto ordine ovviamente, ossia facendo decrescere le potenze di a e facendo crescere quelle di b, o viceversa, per simmetria)

Simpatico vero? Ma non penserete certo che le proprietà del monte Meru siano finite qui? Siamo solo all'inizio e vi devo dire che forse non sono nemmeno state scoperte tutte. Noi, nelle prossime puntate (non so quante), elencheremo le più importanti e qualcuna molto meno conosciuta... Aspettatevi Fibonacci, poligoni vari, frattali e, per non farci mancare niente, anche i celeberrimi numeri irrazionali π ed e.

Alla prossima...

 

QUI gli altri articoli della serie dedicata al Monte Meru (alias Triangolo di Tartaglia)