Categorie: Curiosità Matematica Storia della Scienza
Tags: conica Dandelin ellisse ellissi geometria luogo dei punti
Scritto da: Vincenzo Zappalà
Commenti:15
Una strana uguaglianza ***
Qualcuno si è mai chiesto come facciano a essere vere due definizioni di ellisse che sembrano non avere niente in comune? Sì? Ebbene ecco la risposta. La faccenda, detta in modo molto pratico, si riduce a verificare una strana uguaglianza che vede coinvolti un coltello, un cono, due chiodi, un filo e una matita. I tre asterischi sono dovuti soltanto alla difficoltà di fare disegni tridimensionali all'altezza del compito. Magari qualcuno mi potrebbe aiutare con geogebra...
Esistono due modi diversi per definire in modo "pratico" un'ellisse. Due modi che sembrerebbero del tutto diversi tra loro. Richiamiamoli...
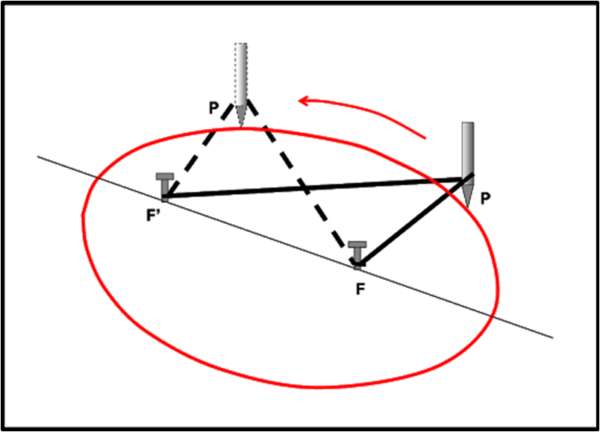
(1) Dati due punti F e F', chiamati fuochi, un'ellissi si costruisce facilmente come luogo di punti che abbiano la somma delle loro distanze dai due fuochi sempre costante. Da cui la celebre costruzione effettuabile con due chiodi, un filo e una matita...
(2) Prendiamo un cono e tagliamolo con un coltello in modo che l'angolo tra il piano del taglio e l'asse del cono sia maggiore della semi apertura apertura del cono. Non per niente l'ellisse è una ... "conica".
Beh... l'unica cosa che sembrano avere in comune è che cambiando la lunghezza del filo o spostando verticalmente il coltello, le ellissi diventano più grandi o più piccole pur rimanendo del tutto simili a loro stesse (ossia non varia l'eccentricità).
E, invece, le due definizioni dicono entrambe la stessa cosa, anche se la dimostrazione appare abbastanza problematica.
Detta in parole estremamente pratiche vogliamo dimostrare che vale la strana uguaglianza:
COLTELLO + CONO = 2 CHIODI + FILO + MATITA
La faccenda è in realtà molto semplice, ma bisogna avere l'idea giusta e ricordare una proprietà delle tangenti tracciate da un punto esterno a una ... sfera. Sfera ? Ma cosa c'entra una sfera? C'entra, c'entra...
In qualche modo siamo di fronte a un ... uovo di Colombo, ma ad avere l'intuizione giusta è stato Germinal Pierre Dandelin, soltanto nel 1822.
Prima di passare alla dimostrazione, vediamo di definire la proprietà appena menzionata. Anzi, per rimanere in tema, utilizziamo proprio un cono!
Consideriamo un punto V e una sfera di raggio r esterna a lui. Tracciamo tutte le tangenti da V alla sfera. Cosa otteniamo? proprio un cono a sezione circolare, come mostrato in Fig. 1.
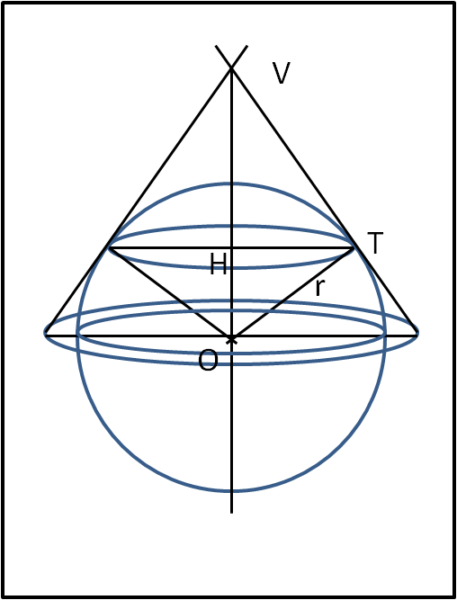
Per costruzione, l’asse del cono passa per il centro della sfera O. I punti di tangenza T descrivono una circonferenza e devono avere la stessa distanza R dal centro O della sfera. Scegliamo un piano passante per V, per O e per un qualsiasi T, come quello riportato in figura. I triangoli HOT (con HO in comune e l’angolo in H retto) sono tutti uguali e quindi lo sono anche i segmenti HT. sono, perciò, uguali anche i triangoli VHT, che hanno VH in comune. Ne segue che VT è sempre lo stesso per ogni T. In altre parole:
I segmenti tangenti a una sfera, tracciati da un punto esterno V, sono tutti uguali tra loro.
Abbiamo detto una cosa veramente banale, come si vede nella Fig. 2, tridimensionale.
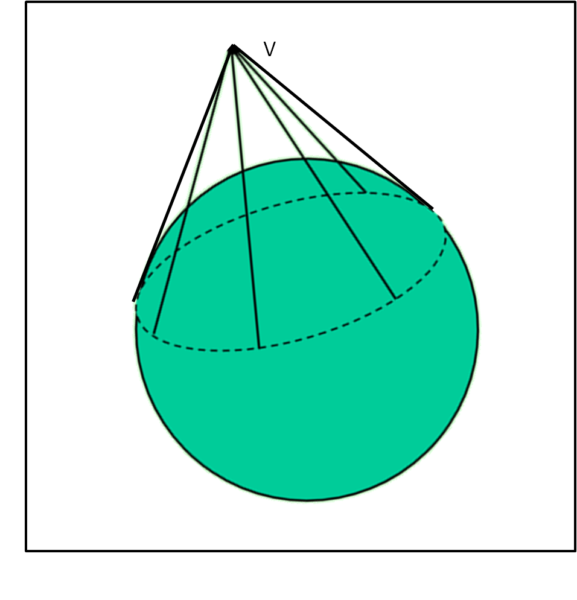
Bene... descritta questa proprietà molto importante, torniamo al nostro cono e al nostro "coltello". Tentiamo di fare un'altra figura a tre dimensioni, la Fig. 3.
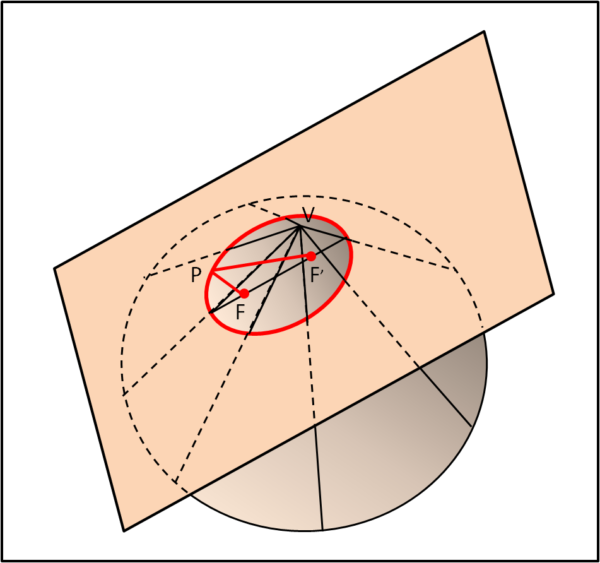
In rosso è stata tracciata la curva che si ottiene attraverso il piano-coltello rosa. Per dimostrare che le due definizioni di ellissi sono veramente la stessa identica cosa, basta dimostrare che esistono due punti F e F' tali che la somma delle distanze di un punto P qualsiasi dell'ellissi ottenuta con il coltello sia proprio una costante, ossia:
PF + PF' = cost.
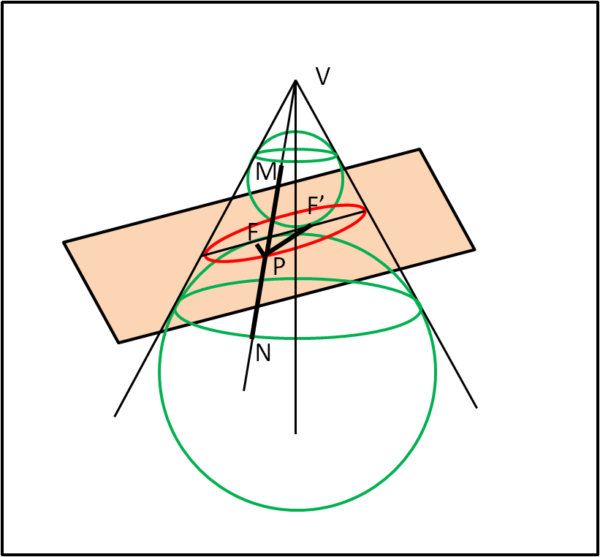
Non sembrerebbe cosa immediata... ma, vediamo di fare tesoro delle Fig. re 1 e/o 2. Per far ciò inseriamo una sfera più grande che sia tangente al cono e al piano del coltello, ma che stia sotto al piano. Per non farci mancar niente, inseriamone un'altra, più piccola. che sia anch'essa tangente al cono e al piano del coltello, ma che stia sopra al piano. In Fig. 4 vediamo una sezione secondo un piano che contenga l'asse del cono (ne possiamo trovare infinite e tutte uguali tra loro... quindi ne basta una).
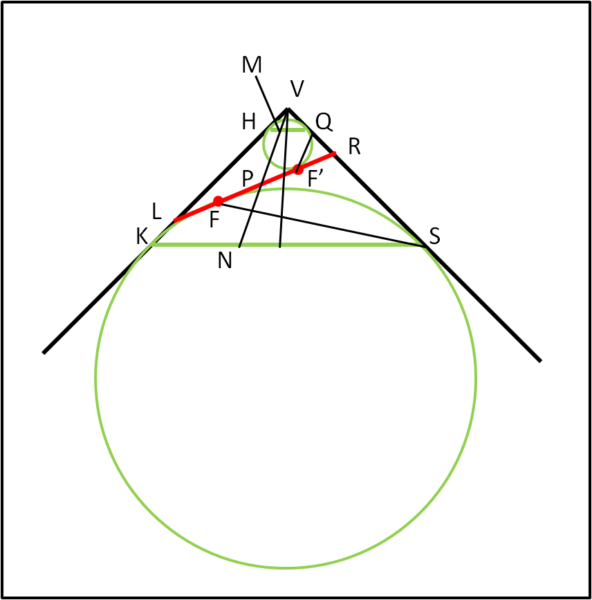
Non facciamoci ingannare dalla figura che è solo una proiezione. L'ellissi tagliata col coltello è la linea rossa inclinata. Il punto P la descrive passando sia da L che da R.
Cosa possiamo dedurre da questa figura? Innanzitutto che il cono e le due sfere sono tangenti lungo le due linee spesse verdi orizzontali (HQ e KS) rispettivamente, che altre non sono che le due circonferenze mostrate "di taglio". Il che vuole dire che la distanza HK si mantiene per qualsiasi punto delle circonferenze tangenti
HK = MN = QS = cost.
Ricordiamo anche che tutti i punti dell'ellissi stanno sul cono e che, quindi, qualsiasi linea generatrice del cono deve passare per i due punti di tangenza e per un punto dell'ellissi. In breve: HL e KL devono stare su una stessa linea (HKL sono allineati), così come PH e PN e QR e RS. Possiamo, perciò, scrivere:
HL + LK = MP + PN = QR + RS = cost.
Abbiamo praticamente concluso che mentre il punto P si muove lungo l'ellisse rossa, la somma delle sue due distanze dai punti di tangenza con le circonferenze verdi rimane costante.
Di seguito la Fig. 5 che ripete la Fig. 4 in tre dimensioni, relativamente al solo punto P (generico).
Accidenti, siamo riusciti a tirar fuori dal cappello una somma di distanza che rimane costante. Tuttavia, i punti da cui misurare le distanze si stanno muovendo lungo due circonferenze... Dobbiamo fare ancora uno sforzo.
Consideriamo, allora, il piano rosa del coltello che origina l'ellissi. Anch'esso è tangente alle due sfere, ma solo e soltanto in due punti, F e F'.
E qui caliamo il jolly! I due segmenti PN e PF sono due segmenti tangenti alla sfera grande tracciati a partire da un punto esterno alla sfera, ossia proprio P. Ma... sappiamo ormai molto bene che questi due segmenti devono essere uguali tra di loro! Tuttavia, la stessa considerazione vale per la sfera piccola. I due segmenti ad essa tangenti, cioè PM e PF' devono essere nuovamente uguali. In parole matematiche molto banali:
PN + PM = RF' + RF = costante
Ma lo stesso identico discorso vale per tutti gli altri punti dell'ellisse, ossia LK = LF e LH = LF', ma anche RQ = RF' e RS= RF. In definitiva:
RF' + RF = LF + LF' = PF + PF' = cost.
Che dice semplicemente che la somma delle distanza dei punti di un'ellissi da due punti detti fuochi (F e F'), che stanno nel piano dell'ellissi, è una costante.
Insomma...
coltello + cono = due chiodi + filo + matita
P.S.: Questo metodo ricorda in parte QUELLO ben più complesso e intrigante utilizzato da Feynman per ricavare la traiettoria orbitale dei pianeti







15 commenti
Bella questa e quando una dimostrazione la si capisce diventa stupenda ahahahah. Però ho come l'impressione che ci si arrivi a rimorchio della prima o sbaglio?
caro Franky,
se intendi dire che conoscendo la proprietà delle tangenti tracciate da un punto esterno a una sfera il resto viene automatico, posso ribadire che è proprio un uovo di Colombo. Ma mentre la prima proprietà era ben conosciuta, la sua applicazione ha dovuto aspettare fino al 1822. Non sempre quello che appare ovvio a posteriori lo è anche a priori...
Miiiiiiii devo imparare a stare zitto, mi dai piú credito di quanto merito. Intendevo che conoscendo la prima dimostrazione dell ellisse é piú facile cercare la seconda. Un poco come il teorema di Pitagora, ormai siamo a circa 50 differenti dimostrazioni ma la prima é stata tutta un'altra storia.
ho capito, ho capito... Ma qual è stata la prima dimostrazione del teorema di Pitagora? Boh...???
Non importa, chi lo ha dimostrato avendo già la soluzione in tasca ha avuto la strada tracciata non che che questo renda banale una simile dimostrazione. In questo caso invece mi pare di capire, dalla tua risposta, che dimostrazione sia comunque un colpo di genio. Giusto?
Beh sì! Però, quale consideri la PRIMA dimostrazione di un teorema che è stato chiamato di Pitagora da noi figli della scuola greca... ?
Non andare sul difficile che mi perdo, probabilmente tutte le dimostrazioni "recenti" fanno parte della categoria "facile" e comunque per me impossibili. A dopo vado ad accompagnare il giardiniere.
Quando tornerai senza giardiniere, beccati questa dimostrazione del teorema detto (da noi) di Pitagora. Il fatto è che risale sicuramente a una data precedente il 1000 a.C.
Tra parentesi si chiama "teorema kou ku"....


Per non parlare, poi, della celeberrima tavoletta babilonese...
Ma anche in India, tra l'800 e il 600 a.C., si scriveva:
La fune tesa per la lunghezza della diagonale di un rettangolo forma un'area pari alla somma di quella formata dal lato verticale e da quello orizzontale.
Quando la finiremo (io compreso) di studiare la storia della Scienza, credendo noi "occidentali" i più bravi per definizione? E questo mi ricorda di quando un nostro "politico" disse che la cultura occidentale era senza ombra di dubbio superiore a qualsiasi altra...
Quella che presumo sia cinese non l'avevo mai vista, mentre quella indiana devo averla sentita da Odifreddi. Quel che dicono i politici vale ben poco, è sempre dettato da un tornaconto e indipendentemente dal loro colore politico. Beh la scienza "moderna" è nata in occidente e pure il principale veicolo della scienza, la stampa a caratteri mobili, è nato in occidente. Se alcuni popoli si sono addirittura rifiutati di usarla non è colpa, almeno questo, dei nostri politici. Parlando di scienza, cultura è un termine difficile da connotare in assoluto, se tutti questi popoli ci hanno preceduto in alcune cose, di certo le hanno mantenute a carattere elitario e i risultati sono le situazioni che si trovano ad affrontare ora. Come sai ho viaggiato parecchio e conosco bene le condizioni medie di vita delle popolazioni ad oriente, chi ha visto Benares non vuole vedere Calcutta. Riassumo brevemente quel che mi pare sia successo: in Europa ad un certo punto e a seguito della diffusione del pensiero grazie alla stampa, qualcuno a cominciato ad alzare il dito medio ai re e al papa mentre.Ad oriente, vi è stato un ambiente più favorevole per appartenenti ad etnie diverse da quella dominante, ma tutto è rimasto relegato ad un livello elitario. Dobbiamo riprenderci Gerusalemme ahahahahaha.
Sarà... sarà...
al momento, il futuro non sembra, però, dare ragione all'occidente... Vedremo... ops... vedrete e vedranno. Quanti secoli è durato questo vantaggio occidentale? I nostri secoli si dilatano e quegli degli altri si accorciano! Cosa era l'occidente per secoli e secoli in cui la società progrediva in oriente? Parlo prima dei greci, ovviamente...
Al momento il futuro nessuno lo conosce, politicamente l'oriente è chiuso in casa dalle 7 flotte navali + le due non convenzionali, americane. Quale vantaggio? Se intendi quello scientifico voglio proprio vedere con la chiusura universitaria e di ricerca messa in atto dagli USA verso la Cina quanto riusciranno a progredire da soli con un sistema oppressivo come il loro, per ora hanno preso tutto e dato nulla. Si d'accordo cultura millenaria ma sempre elitaria era e su questo aspetto da loro abbiamo poco da imparare, per ora. In tutta la loro saggezza culturale antica, che poi non è così antica come si crede, qualcosa si deve essere inceppato altrimenti saremmo noi a rincorrere.
Buongiorno, non dimentichiamo che importanti porzioni della scienza occidentale sono dovute agli arabi che in qualche modo hanno trasmesso e sviluppato la conoscenza greca (a sua volta stimolata da contatti con altre civiltà). La civiltà occidentale è da molto tempo ormai vittima di una frenesia vorace e vorrebbe primeggiare su tutto, forse aveva ragione Jaspers considerandola terrorizzata da un declino già scritto nel suo appellativo stesso ("occidentale", cioè "al tramonto") e quindi disperatamente tesa a sottrarsi alla decadenza. Guardando però a come si sta evolvendo la società cinese sembrerebbe che anche loro si stiano "occidentalizzando". Ad essere decadente parrebbe essere tutta o quasi la civiltà umana, a dispetto del progresso tecnologico galoppante.
Sono il pensiero e la conoscenza condivise che devono progredire e su questo mi pare ci sia davvero tanta strada da percorrere.
caro Guido,
non per niente il mio idolo storico è Federico II... la fusione delle varie culture nella città di Palermo, sotto il suo regno, dovrebbe insegnare molto...
Preferisco precisare che la scienza nel significato attuale nasce con Galileo, tanto di cappello a quel che arriva da prima ma chiamarla scienza come quella che si intende oggi mi pare fuorviante. Sorry Guido ma questa diffusa tendenza a vedere sempre meglio quel che viene da fuori mi sa tanto di mancanza di esperienza del "fuori".
Una visione non manualistica di Federico II:
https://www.youtube.com/watch?v=glt7o_Q5qHw