Questo articolo è stato inserito nell'archivio nella sezione Meccanica Celeste.

Questo articolo è una delle tante "ciliegine cosmiche" che potete gustare QUI

Il linguaggio usato da Galileo per descrivere la caduta dei gravi o il moto di un grave al quale è stata impartita una certa velocità è diverso dal linguaggio usato da Newton per descrivere la "sua" forza di gravità? Sì oppure no? Discutiamone giocando con proiettili, missili intercontinentali e sonde spaziali.

Quante volte abbiamo parlato del moto parabolico? Lo abbiamo fatto sia nel blog che nel libro "La Fisica addormentata nel bosco". E' veramente un classico e si deve a Galileo Galilei una sua trattazione estremamente accurata. Una descrizione che ci fa capire come Galileo avesse intuito che esisteva un qualcosa che faceva muovere le cose in un certo modo. Il grande pisano era riuscito a descrivere questi moti da un punto di vista essenzialmente cinematico, non cercando il perché, ossia non entrando nella dinamica.

Newton, invece,  introduce una forza agente tra cose diverse, che permette di spiegare il perché del movimento. Galileo e Newton dovrebbero perciò essere completamente d'accordo anche se su piani differenti. Ma è proprio così? Ci abbiamo riflettuto sopra abbastanza bene?

Andiamo a riprendere una celebre figura di Newton, fondamentale per tutta la meccanica celeste futura, quella in cui il grande genio ci mostra come a furia di lanciare una "pallina" dalla cima di un monte essa, se la sua velocità è sufficientemente elevata, riesce a immettersi in orbita circolare. Sicuramente il punto di partenza per i futuri viaggi verso il Cosmo sia per la messa in orbita dei satelliti artificiali sia per la visita agli altri pianeti del Sistema Solare, in attesa di quelli verso altre stelle o, addirittura, galassie.

 

 

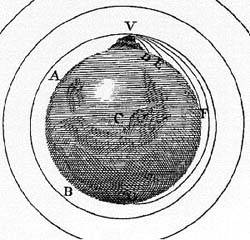
Ci accorgiamo che tutto si riduce, per modo di dire, all'utilizzo delle "coniche", ossia di quelle figure geometriche conosciute fin dall'antichità e che possono essere introdotte in svariati modi, sia "fisici" che puramente "matematici".  Portiamoci allora su una vetta di un monte con una pallina in mano e poi cerchiamo di imitare Newton, ricordando Galileo.

Con l'aiuto, magari, di Superman, lanciamo una pallina con velocità orizzontale crescente. All'inizio sembra che tutto vada secondo quanto descritto da Galileo: la pallina percorre una traiettoria parabolica (metà parabola, in realtà) fino a cadere sulla pianura circostante. Aumentando la velocità del lancio la parabola si apre sempre di più (ma sempre parabola è, ossia la sua eccentricità resta uguale a UNO).

Poi, entra in scena Superman che riesce a trasformare questa traiettoria in un cerchio e crea un satellite artificiale. Cerchio vuole anche dire eccentricità uguale a ZERO. C'è qualcosa che non va... aumentando gradatamente  la velocità riusciamo a passare da un'eccentricità uguale a UNO a un'eccentricità uguale a ZERO. No, no... questo salto improvviso non può convincere. Il linguaggio usato da Galileo, che sembrava essere perfetto, viene stravolto da quello di Newton. Chi dei due sta sbagliando?

Rispondendo in modo drastico e molto semplicistico potremmo dire che sbaglia Galileo, ma la faccenda va studiata più attentamente. In tale modo ci accorgeremo che stiamo diventando degli astrodinamici, seppure molto "rozzi". Ricordiamo, infatti, come conferma anche Wikipedia, che:

"L'astrodinamica è la disciplina che studia il moto dei razzi, dei missili e dei veicoli spaziali determinato a partire dalle leggi del moto e dalla legge di gravitazione universale di Isaac Newton. Concerne in particolar modo gli oggetti artificiali e lo studio delle loro traiettorie"

La nostra pallina è, in parole molto povere, un vero e proprio veicolo interplanetario artificiale, in quanto, anche senza bisogno di carburante (basta la forza di Superman), può benissimo eseguire le azioni principali descritte dall'astrodinamica.

Vediamo, allora, di affrontare il problema in modo estremamente generale e sistemiamo la nostra pallina P a una certa distanza da una massa concentrata in un punto F (come dice anche Newton). Utilizziamo la Fig. 1 (dove vi è anche un esempio numerico):

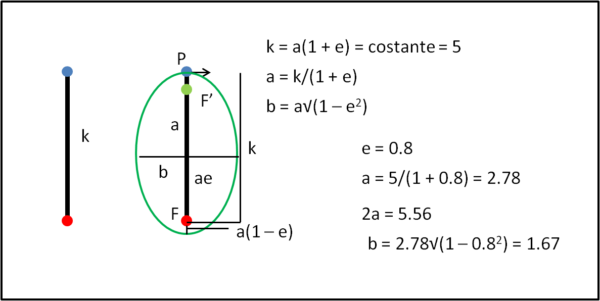
Insieme a Superman noi stiamo vivendo in un mondo speciale (Universo parallelo?), che non subisce l'enorme forza di gravità  del punto F (assumiamo che la sua massa sia pari a quella di tutta la Terra), e quindi ci possiamo permettere di lasciare andare la pallina al suo destino ed entrare nel mondo di Newton. Bene la pallina non fa altro che cadere addosso a F e rimanerci. Essa ha descritto un segmento PF. Galileo sarebbe anche d'accordo, anche se non ha mai potuto provarlo con i suoi esperimenti.

Impartiamo adesso, per semplicità, una piccola velocità in direzione perpendicolare alla congiungente PF. La pallina dovrebbe seguire quanto detto da Galileo, ossia descrivere una parabola. E, invece, fa ben altro, seguendo Newton: essa descrive un'ellisse attorno al punto F. Al cambiare della velocità si modifica l'ellisse, ma deve sempre valere la condizione:

PF = k (costante)

dato che il punto di partenza della pallina e il punto dov'è concentrata la massa rimangono sempre gli stessi.

Come possiamo disegnarla? Niente di più facile, basta ricordare le formule più semplici legate all'ellissi. La distanza tra un fuoco (nel nostro caso il punto F, dove è concentrata la massa)  e il punto P iniziale deve essere dato dalla distanza massima tra di loro che è data da:

PF = a(1 + e) = k

Da cui:

a = k/(1 + e)

Al variare della velocità varia l'eccentricità e, di conseguenza, anche il semiasse a. Non ci resta che scegliere una certa eccentricità e calcolare il valore di a. Una volta fatto questo diventa banale anche il calcolo di b, dato che:

b = a√(1 - e²)

Nella Fig. 2, abbiamo disegnato le ellissi ottenute, mantenendo PF costante, per e =0.8, 0.5, 0.2 e 0.0.

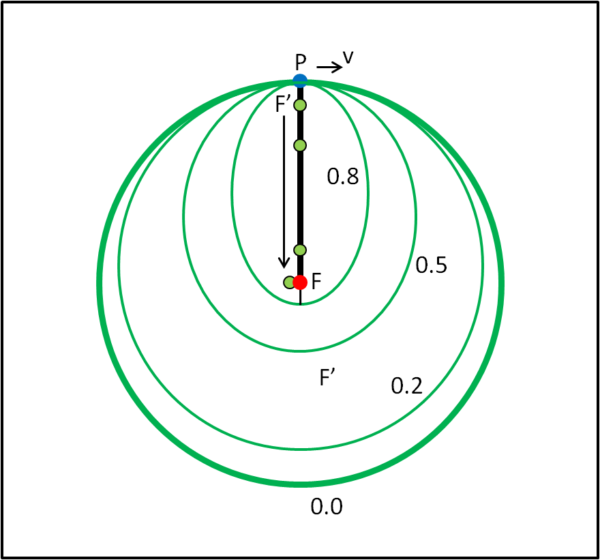
Ovviamente, per e = 0, la nostra traiettoria diventa un a circonferenza e il Fuoco F' (punto verde, variabile a seconda della e e della a, ossia della velocità impartita in P) coincide con F. Questa circonferenza è stata tracciata più spessa.

Possiamo anche dire che, non essendo del tutto sprovveduti, abbiamo scelto P come punto di massima distanza da F per potere impartire una velocità relativamente piccola.

Tuttavia, ormai ci abbiamo preso gusto e Superman aumenta ancora la velocità. Cosa vuol dire in pratica? Che stiamo considerando il punto P come quello avente la minima distanza da F e quindi il calcolo dell'orbita deve seguire la formula:

PF = a(1 - e) = k

a = k/(1 - e)

Come fatto prima possiamo continuare a far crescere la nostra velocità e quindi anche a e b...

Sì, ma ci troviamo di fronte a un'altra orbita particolare, quella che si ottiene per e = 1. In tal caso, infatti, a tende a infinito e l'ellissi diventa una parabola di fuoco F (Fig. 3)

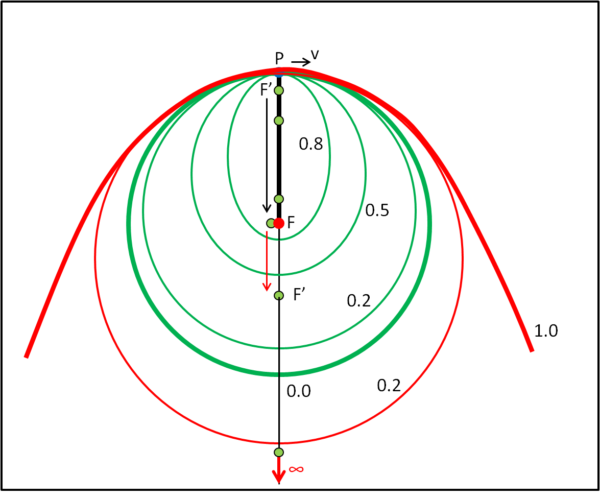
Notiamo anche che il segmento descritto a velocità uguale a ZERO, implica nuovamente che e sia uguale a UNO.

Infatti, la distanza tra P e F è anche il doppio del semiasse, ossia 2a:

Ma  PF è anche la distanza tra i fuochi  e abbiamo, ricordando che la distanza tra fuoco e centro dell'ellisse è  uguale ad ae :

PF = k = 2ae

Ne segue che:

2a = 2ae

Quindi e = 1

Una strana ellisse degenere di eccentricità uguale a 1. La Fig. 2 mostra perciò tutti i valori possibili per l'eccentricità che varia tra 0 e 1.

Nulla toglie, però, che il nostro Superman continui nella sua "fatica" (ormai c'ha preso gusto). Basta che impartisca una velocità maggiore che implichi un'eccentricità maggiore di UNO. La traiettoria diventa un'iperbole.

In tal modo non solo usciamo facilmente dal campo gravitazionale di F, ma anche da quello di un certo oggetto S, attorno a cui ruota il nostro F. E se esageriamo ancora si potrebbe anche uscire dal campo gravitazionale di G, attorno a cui ruota S.

Non vi è certo sfuggito che F può essere considerata la Terra, S il Sole e G la Via Lattea. Insomma, in compagnia di Superman abbiamo fatto un po' di astrodinamica e abbiamo anche fatto conoscenza con le velocità cosmiche.

La prima velocità è quella che permette di entrare in orbita circolare attorno alla Terra. Essa è pari a 7.9 km/s. Se la superficie sferica fosse completamente liscia e sferica sarebbe la velocità di una satellite artificiale che volasse a ZERO metri di altezza dal suolo.

Abbiamo, poi tutta una serie di ellissi, con fuoco nel centro della Terra, fino alla seconda velocità cosmica, quella capace di immettere in orbita parabolica. Essa è la ben nota velocità di fuga della Terra e vale 11.2 km/s.

Se poi vogliamo uscire anche dalla gravità solare, come abbiamo già visto QUI, dobbiamo raggiungere la terza velocità cosmica, pari a 16.7 km/s (valore minimo).

Al momento ci interessa poco, ma esiste anche una quarta velocità cosmica che è quella in grado di farci lasciare anche il campo gravitazionale della galassia, che vale  circa 129 km/s. Con questa velocità si potrebbe raggiungere anche la galassia di Andromeda, ma chi ce lo fa fare, dato che la nostra vicina di casa sta ormai entrando in contatto con noi? Basta solo aspettare un "pochino".

Torniamo, però, al punto iniziale del nostro problema: cosa succede per velocità minori della prima? Beh, basta "espandere" il punto F fino ad avere le dimensioni della Terra. La nostra montagna di partenza ridiventa solida come mostrato in Fig. 4, che altro non è che quella celebre di Newton!

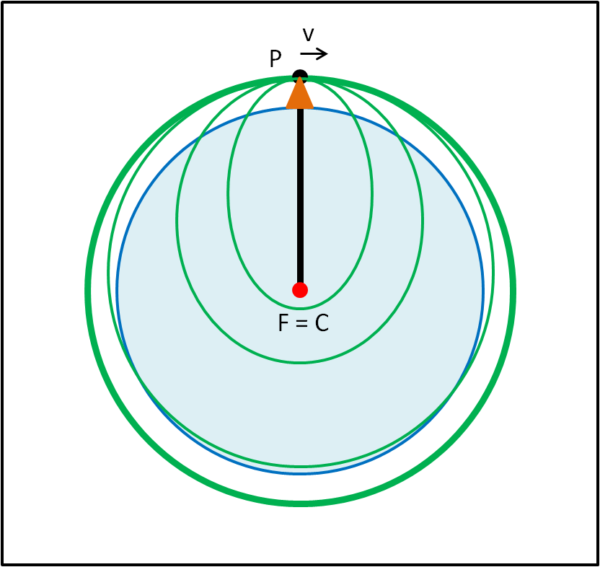
Il punto F coincide, ovviamente, con il centro della Terra C. Le traiettorie sono tutte ellissi, "bloccate" dalla superficie terrestre.

Insomma, concludendo, non esiste alcun moto parabolico nella caduta dei gravi a meno di non usare una velocità di lancio (o "di sparo") pari a quella di fuga della Terra. Le traiettorie descritte così bene da Galileo sono ellissi (o -meglio- pezzi di ellissi). Pezzi di ellisse, però, che possono quasi perfettamente essere approssimate da pezzi di parabola. Infatti, l'approssimazione fatta da Galileo era, in fondo, solo e soltanto quella di considerare una suolo perfettamente orizzontale. In altre parole, considerare la Terra come una sfera di raggio infinito. Automaticamente, la traiettoria diventa una parabola.

Povero Galileo... un'errore più che accettabile (e lo si continua a fare anche oggi) fino a che si ha a che fare con lanci del martello, proiettili di un fucile o palle di cannone. Una differenza non trascurabile esiste già quando si ha a che fare con missili intercontinentali (e in parte già con i tristementi noti missili nazisti V2...). Teniamo conto che i missili sono dotati di propulsione propria e di un sistema a più stadi. Tuttavia, nulla vieta di prospettare l'intera faccenda nel caso di un lancio basato solo su un impulso iniziale.

Insomma, il linguaggio può considerarsi lo stesso (solo una certa sfumatura... dialettale, al massimo) e intanto, però, oltre che assolvere Galileo siamo riusciti a fare una plausibile astrodinamica con due soli asterischi!

Vi è venuta voglia di fare due chiacchiere con Newton e Galileo?

QUI e QUI troverete i nostri dialoghi (im)possibili.