Il presente articolo è stato inserito nella pagina d'archivio  "Antichi Greci, che passione!"

 

Il teorema di Talete porta con sé un po' di ambiguità, dato che quello che noi italiani chiamiamo "teorema di Talete" è diverso da quello  "inglese". Dimostriamo quest'ultimo e ci accorgeremo che si devono dimostrare anche altri enunciati, che siamo soliti dare per buoni. Un'interessante modo per capire quanta logica ci sia nelle scoperte geometriche degli antichi greci (ma non solo loro, anche degli indiani, dei cinesi, degli arabi...)

Ricordiamo, innanzitutto, la differenza tra assiomi e teoremi.

Assioma è un qualcosa che si dà per giusto, senza alcun bisogno di dimostrarlo. Utilizziamo il significato esatto che ne davano gli antichi greci, facendo riferimento al trattato fondamentale Elementi di Euclide:

"Gli assiomi enunciano delle verità, non dimostrabili, evidenti a chiunque. In altre parole, essi possono essere considerati delle NOZIONI COMUNI da accettare perché talmente evidenti da rappresentare la realtà senza ombra di dubbio.

Un teorema è invece un'enunciazione, non completamente evidente, che può essere dimostrata a partire da un assioma attraverso implicazioni logiche.

Fatte queste doverose premesse, affrontiamo l'argomento che ci interessa: Il teorema di Talete.

E qui sorge l'ambiguità. Nelle scuole italiane si definisce come tale ciò che capita ai segmenti di un fascio di rette parallele tagliate da due trasversali . Nelle scuole anglosassoni si definisce, invece, teorema di Talete il fatto che qualsiasi triangolo inscritto in un cerchio (e lo sono tutti), che abbia per base un diametro, deve essere rettangolo (l'angolo retto è quello opposto al diametro).

In realtà, entrambi si attribuiscono a Talete e noi vogliamo dimostrare quello di lingua inglese, attraversando vari concetti e affermazioni che si danno troppo spesso per scontate. Enunciati semplicissimi che vengono a mano a mano dimostrati prima di arrivare alla conclusione.

L'assioma che ci serve come punto di partenza prende il nome di ISOMETRIA ed è spiegabile molto facilmente. Prendiamo una figura geometrica qualsiasi, ad esempio un triangolo. Bene, possiamo traslarlo nello spazio euclideo o possiamo anche ruotarlo, ma lui rimane sempre lo stesso, ossia la sua forma e le sue caratteristiche (lati e angoli) rimangono inalterati. Se sdoppiamo un triangolo e facciamo traslare e/o ruotare la sua "copia" perfetta (totalmente sovrapponibile a quello di partenza) essa rimane sempre uguale a quella iniziale (per essere precisi "congruente"). In realtà, bastano alcuni dati (due lati e l'angolo compreso, ad esempio) per essere sicuri che due triangoli rimangano congruenti (principi di uguaglianza) pur traslando e ruotando.

Che questo sia un assioma valido è facilmente accettabile, dato che si può eseguire a ritroso una traslazione e/o una rotazione per riuscire a far nuovamente coincidere le due copie.

Prima di partire in quarta, poniamoci un problema molto interessante: ci troviamo di fronte a una circonferenza perfetta. Come facciamo a trovarne con esattezza il centro? Facilissimo, come illustra la Fig. 1.

 

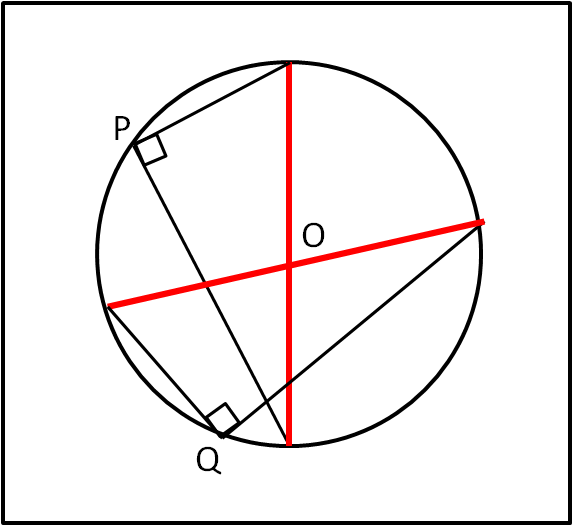
Prendiamo un punto P qualsiasi della circonferenza e da lui tracciamo due rette tra loro perpendicolari (che intersechino la circonferenza in due punti). Se tracciamo la congiungente di questi due punti siamo sicuri che il centro deve stare su di essa, dato che abbiamo di fronte un triangolo rettangolo la cui ipotenusa deve essere un diametro, proprio per il teorema di Talete (quello inglese). Basta scegliere un altro punto Q sulla circonferenza e ripetere l'operazione. Troveremo un altro diametro e la loro intersezione non può che essere il centro O. Un metodo molto rapido ed elegante che si basa proprio sul teorema che vogliamo dimostrare. Un teorema, perciò, decisamente molto utile e molto utilizzato!

Prendiamo perciò un bel triangolo qualsiasi, sdoppiamolo e poi trasliamolo mantenendo un lato parallelo a quello originario. Otteniamo la Fig. 2

Per l'assioma utilizzato come punto di partenza, i due triangoli devono avere sia i lati che gli angoli uguali (sono congruenti) e, di conseguenza, gli angoli a e a' devono essere uguali.  Il risultato può generalizzarsi a qualsiasi triangolo e, quindi, vale l'enunciato che gli angoli corrispondenti di due rette parallele tagliate da una trasversale sono uguali tra loro.  L'uguaglianza vale, ovviamente, anche per angoli ottusi.

Concentriamoci sulla Fig. 3.

Per definizione stessa di angolo piatto (180°), esso è un angolo tra due semirette che appartengano alla stessa retta. Ne segue che la somma dei due angoli a e b deve essere di 180°. Ma anche la somma di a e dell'angolo c deve essere uguale a 180°. In formule veramente banali:

a + b = 180°

a + c = 180°

Sottraendo la seconda espressione dalla prima:

0 + b - c = 0

c = b

Generalizzando, nuovamente, il risultato possiamo concludere che due angoli opposti al vertice sono uguali.

La  stessa Fig. 3 ci permette, immediatamente, di concludere che gli angli alterni interni ed esterni formati da due rette parallele tagliate da una trasversale sono anch'essi uguali tra loro.

Infatti, per quanto appena detto a è uguale a d, ma sappiamo anche che a è uguale ad a', quindi a'  è uguale a d (angoli alterni interni). Analogamente:

c' = c

c = b

da cui:

c' = b         (angoli alterni esterni)

Torniamo al nostro triangolo iniziale, sapendo molte cose in più, disegnando la Fig. 4.

La somma degli angoli a', b' e c' è uguale a 180°. Ma i tre angoli sono uguali ai tre angoli del triangolo (uno in comune e due alterni interni). Ne segue l'importantissima conclusione che la somma degli angoli interni di un triangolo qualsiasi è sempre uguale a 180°. Ovviamente, in ambito euclideo.

Ridendo e scherzando abbiamo dimostrato, partendo da un'assioma semplicissimo, una delle proprietà più utilizzate in geometria. Quando diamo per scontato qualcosa, pensiamo sempre bene a cosa ci stia realmente dietro e quanto sia raffinata la logica con cui sono state enunciate certe affermazioni che oggi usiamo senza porci più alcun dubbio.

Proseguiamo nel nostro cammino di pura logica.

Consideriamo un triangolo molto particolare, facilmente costruibile: un triangolo isoscele. Per definizione esso è un triangolo qualsiasi che ha due lati uguali tra di loro. Lo sono anche gli angoli opposti ai due lati uguali. Possiamo facilmente dimostrarlo, utilizzando l'assioma di partenza, in Fig. 5.

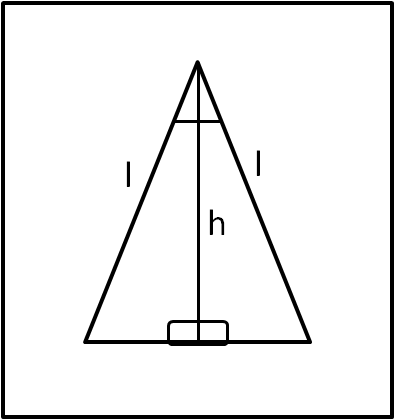
Tracciamo la bisettrice dell'angolo opposto al lato "diverso". Otteniamo due triangoli. Essi, tuttavia, devono essere congruenti per uno dei criteri di uguaglianza: un lato in comune, un lato uguale per costruzione e l'angolo fra di loro, dato che è stato ottenuto dividendo esattamente a metà un certo angolo qualsiasi di partenza. Sono quindi uguali gli angoli opposti ai lati uguali. Tra parentesi, devono anche essere uguali gli angoli compresi tra la bisettrice e il lato "diverso". Ma, la loro somma, per definizione di angolo piatto, deve proprio essere 180°. Ne segue che la loro ampiezza deve essere 180°/2 = 90°. In un triangolo isoscele la bisettrice e anche mediana, altezza e asse del lato "diverso".

Stiamo dicendo cose che oggi sembrano ovvietà, ma quanta logica e acutezza di mente era necessaria per chi stava descrivendo, partendo praticamente da zero, lo spazio in cui viveva. Questo tipo di analisi, mi permetto di dirlo, dovrebbe essere usata nelle scuole elementari e medie... Forse la matematica e la geometria avrebbero molti più "simpatizzanti".

Non abbiamo ancora finito, ma ci siamo vicini...

Disegniamo finalmente un bel cerchio di centro O, tracciamone un diametro AB e consideriamo un punto C qualsiasi sulla circonferenza (Fig. 6).

Uniamo C con A e con B, ottenendo, ovviamente, un triangolo ACB. Vogliamo calcolare quanto misura l'angolo c . Tracciamo il raggio OC. Esso, per definizione di raggio, deve essere uguale a OA e a OB. I due triangoli ACO  BCO sono, quindi, entrambi isosceli. Il che vuole anche dire che sono uguali gli angoli  opposti al vertice O. L'angolo c è, perciò, dato dalla somma di a e di b. Abbiamo appena dimostrato, però, che la somma degli angoli di un triangolo qualsiasi deve essere di 180°. Possiamo perciò scrivere:

a + b + c = 180°

ma

a + b = c

per cui:

2c = 180°

c = 90° 

per qualsiasi triangolo che abbia un diametro come lato e il vertice opposto sulla circonferenza.

Ovviamente, anche il "nostro" teorema di Talete richiederebbe una dimostrazione altrettanto semplice e logica...

Prenotiamoci per una prossima volta.