Categorie: Relatività
Tags: equazione di campo forza apparente principio di equivalenza Relatività Generale al microscopio
Scritto da: Vincenzo Zappalà
Commenti:20
La Relatività Generale al microscopio. 1: Le basi **
Questo è il terzo articolo della serie "La Relatività Generale al microscopio"
Prima di entrare nella formula vera e propria riassumiamo alcuni concetti che ci accompagneranno lungo tutto il viaggio.
Riassumiamo i pochi concetti fondamentali, punto di partenza obbligatorio per la comprensione della Relatività Generale.
Principio di equivalenza
Attraverso imbianchini che cadono e riflessioni profonde, Einstein asserisce che niente e nessuno potrebbe notare la differenza tra un campo accelerato e un campo gravitazionale. Ciò è riassunto nella semplice Fig. 1, dove chi è posto all'interno di un cabina senza finestre non può rendersi conto se ciò che fa cadere una pietra sul pavimento è un'accelerazione della cabina verso l'alto (la pietra sta ferma, ma è il pavimento che le va incontro) o è, invece, l'accelerazione di gravità diretta verso il basso (il pavimento è fermo, ma la pietra è libera di seguire un percorso obbligatorio).
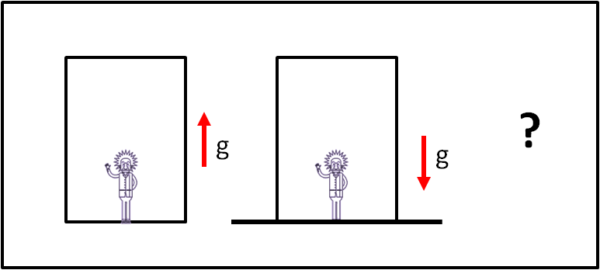
Un concetto fondamentale che dimostra come massa gravitazionale e massa inerziale siano VERAMENTE la stessa cosa e che estende il concetto di Galileo, relativo al moto uniforme dei sistemi inerziali (quando diceva che che si muove a velocità costante non potrebbe mai stabilire se si muove lui o tutto ciò che lo circonda), anche al mondo accelerato, non inerziale (QUI la pagina d'archivio che raccoglie molti articoli dedicati al principio di equivalenza)
Anche la luce è costretta a curvare
Immaginiamo che in un ascensore che è accelerato verso l'alto venga "sparato" un raggio di luce (Fig. 2). Essa, per chi sta fuori dall'ascensore percorre una linea retta. Ma chi sta dentro all'ascensore vede le cose in modo ben diverso. A causa dell'innalzamento continuo del pavimento il raggio di luce (chiamiamolo pure fotone) cambia la sua distanza dal pavimento che diventa sempre minore. Oltretutto, dato che la velocità dell'ascensore cresce continuamente, la traiettoria "apparente" della luce per chi è all'interno appare una parabola. La conclusione, che potrebbe far ridere chi sta fuori dall'ascensore, è perciò : "la luce all'interno di un sistema accelerato descrive una traiettoria curva".
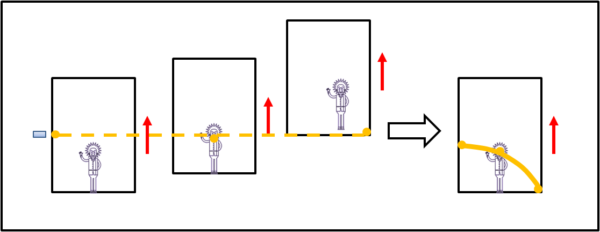
A questo punto entra in ballo il primo concetto, ossia l'equivalenza perfetta tra un ascensore accelerato e un campo gravitazionale. Se all'interno dell'ascensore la luce curva, lo stesso deve accadere all'interno di un campo gravitazionale. Ne segue che se agisce un campo gravitazionale la luce è costretta a seguire una traiettoria curva. Il concetto di forza gravitazionale viene escluso del tutto! La forza di gravità è una forza apparente.
L'eclissi di Sole del 1919
Il Sole causa un campo gravitazionale e quindi deve curvare la luce di una stella che passa al suo interno. Ne segue che questo effetto deve essere visto anche da chi sta sulla Terra, dato che Terra, stella e Sole fanno parte dello stesso sistema di riferimento (possiamo tranquillamente dire che non esiste nessun movimento reciproco avendo a che fare con la luce e la sua enorme velocità). In parole molto rozze, la cabina dell'ascensore diventa il campo gravitazionale del Sole e noi possiamo assistere agli effetti che ne derivano. Una conferma strabiliante (Fig. 3).
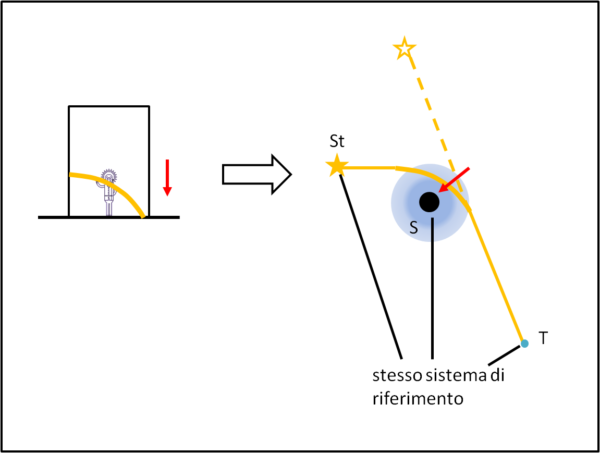
Curvatura dello spaziotempo
Riduciamo lo spazio a una sola dimensione e rappresentiamolo in funzione del tempo (Fig.4). Immaginiamo di muoverci a velocità costante. Nel grafico ciò viene descritto da una linea retta: il rapporto tra distanza percorsa e tempo impiegato a percorrerla è costante. Cosa succede se invece di velocità costante, imponiamo un'accelerazione costante, ossia un aumento continuo della velocità? Otteniamo una traiettoria curva! Tuttavia, sappiamo anche che in un campo gravitazionale si subisce un'accelerazione (principio di equivalenza) e quindi si devono seguire linee curve. Un campo che causa traiettorie curve deve, perciò, essere curvo.
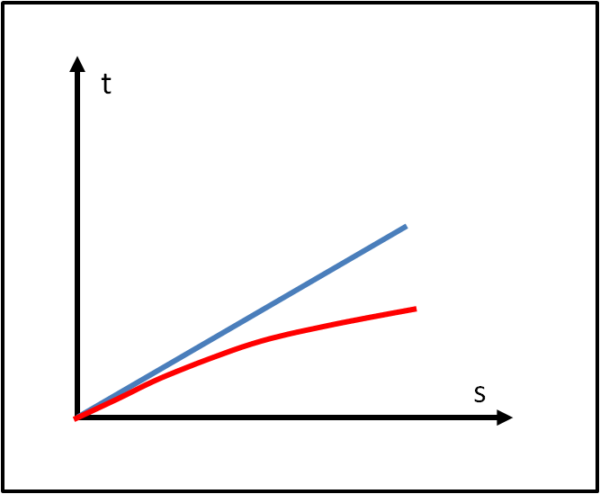
Sintesi semplificata
Tutto l'Universo vive dentro un enorme ascensore (nessuno può vederlo da fuori). Tuttavia, se siamo molto lontani da chi deforma lo spaziotempo, ci muoviamo solo nel tempo in linea retta, dato che la curvatura spaziotemporale non si fa sentire. Se ci avviciniamo a una massa, lo spaziotempo si deforma e siamo costretti a percorrere traiettorie curve che ci obbligano ad accelerare. Tuttavia, ciò che causa l'accelerazione non è una FORZA, ma solo la curvatura dello spaziotempo (vedi anche questo articolo). La forza gravitazionale non esiste. Ovviamente, tutto ciò si riferisce solo al campo gravitazionale e siamo liberi di imprimere altri tipi di forze; ad esempio, mettere in azione un motore che lotti contro la curvatura e ci sposti rispetto allo spaziotempo curvo del punto in cui siamo. Questa è una vera forza e non solo una forza apparente. Teniamo, però, conto che le accelerazioni che imprimiamo noi hanno normalmente effetti ridicoli rispetto a quelle imposte dallo spaziotempo curvo nei pressi di grandi masse (chiedete ai buchi neri).
Tutto l'Universo è un gigantesco "mollusco" che potrebbe anche essere PIATTO, ma che subisce deformazioni più o meno accentuate vicino a grandi masse. L'Universo piatto non interferisce assolutamente con la curvatura spaziotemporale dovuta alla gravità (ossia alla presenza di masse): le due cose possono perfettamente convivere!






20 commenti
Articolo preliminare perfetto!
La "forza geniale" di un grande pensatore (Einstein) sta nei concetti semplici con cui inizia la teoria innovativa.
Poi l'utilizzo di strumenti matematici avanzati serve per quantificare quanto pensato preliminarmente.
Bell'articolo Vincenzo anche per il richiamo alla figura fuorviante del lenzuolo "avvallato" per effetto della massa al centro che non considera la variabile TEMPO
grazie come sempre Michelino...
Lo faccio solo ora perche' oberato da lavoro ed esigenze familiari, per cui da un po' mi limito a leggere. Vorrei esprimere il mio compiacimento per la decisione e il forte interesse per questa serie di articoli sulla RG. Bravo, Prof ! Ti seguo.
grazie Artù... sei sempre un re!!!
Buongiorno, possiamo quindi dire che la "forza" gravitazionale è solo un effetto dovuto ad un campo curvo e che noi interpretiamo questo effetto come se fosse dovuto ad una forza? E che, di conseguenza, vi è coincidenza tra gli effetti dovuti a due cause di natura diversa?
esattamente Guido. La forza di gravità non è una vera forza, ma una forza apparente, così come, ad esempio, lo è la forza centrifuga per il sistema rotante.
Vincenzo volevo un chiarimento considerato che non mi è tanto chiaro quanto da te affermato in un articolo di ottobre del corrente anno " lo spazio tempo la nostra prigione quotidiana":
se ci si muove solo nel tempo e non nello spazio tu hai scritto
Non ci resta che stabilire quale sia questa velocità spaziotemporale che deve rimanere sempre la stessa e che non può assolutamente essere superata (e non si tratta solo di evitare una multa...). Teniamoci forte e non spaventiamoci proprio adesso... questa velocità a cui tutti noi ci stiamo muovendo, senza accorgercene, è la velocità della luce! Portiamoci nella Fig. 3, quella in cui ci si muove sempre e comunque alla velocità della luce.
Forse spiegare il concetto è banale ma non nascondo che non mi è tanto chiaro
caro Michele,
te lo spiego in breve...
Normalmente, in relatività ristretta, al posto del tempo t, si inserisce il prodotto ct (vedi articolo sulla RR), in modo che anche nell'asse del tempo si misuri effettivamente una distanza (è solo una questione di unità di misura, dato che c è una costante). Ma allora, se io mi muovo soltanto lungo questo asse, quale è la velocità? Beh, come sempre spazio diviso tempo, ossia ct/t = c, quindi mi muovo proprio alla velocità della luce. E' una constatazione che deriva dall'aver normalizzato il tempo per poterlo confrontare (e sommare ad esempio nell'invariante relativistico) con lo spazio.
Se vuoi capire ancora meglio, puoi andare nel capitolo della RR "Spazio e tempo per me pari sono". Si dice, in pratica, che
... La nuova unità di tempo T = 1 m, è legata al tempo t espresso in secondi dalla relazione 1 m = c t, da cui si deduce t = 1 m / (300000000 m/s ). La nuova unità “metrica” di tempo corrisponde al tempo che occorre alla luce per percorrere uno spazio di un metro. Un tempo T di 300 000 km corrisponde, quindi, a un secondo...
Attenzione: in tale sistema di unità, la velocità di un corpo è il rapporto fra uno spostamento (in metri) e il tempo (anch’esso espresso in metri), ossia non è altro che il parametro adimensionale β.
Ok Vincenzo molto chiaro come al solito nelle tue spiegazioni/risposte
Buongiorno,
riporto una raffigurazione piana di un generico campo di accelerazione (chiedo lo sforzo di fantasia di ignorare lo sfondo “terrestre”), cioè di una regione ipotetica in cui ogni punto è caratterizzato da uno specifico valore di accelerazione (il valore del modulo del vettore accelerazione). Le isolinee uniscono i punti aventi uguale modulo del vettore accelerazione. Come si vede vi sono aree in cui il modulo ha valore negativo e aree in cui il modulo ha valore positivo. Vi sono poi linee che uniscono i punti con modulo nullo, riportate in verde. Un ipotetico sistema di riferimento ubicato lungo tali linee sarebbe caratterizzato da accelerazione nulla, e pertanto per esso varrebbero le relazioni stabilite dalla RR. Un ipotetico sistema di riferimento ubicato in qualunque altro punto del campo sarebbe caratterizzato da accelerazione non nulla, e pertanto per esso varrebbero le relazioni stabilite dalla RG. E' corretto?
direi proprio di sì, caro Guido... La linea identificata in tal modo sarebbe, comunque, uno spaziotempo a 4 dimensioni rappresentabile con Minkowski.
Quindi in corrispondenza delle isolinee di "zero" lo spaziotempo 4D può essere descritto con la geometria euclidea (campo piano=tangente nel punto al campo curvo) e nelle altre aree lo spaziotempo non può essere descritto con la medesima geometria ma richiede una geometria non euclidea. Va bene?
Non proprio euclidea, in quanto vale la relatività ristretta. Chiamiamola quasi-euclidea (segue il diagramma di Minkowski).
OK, grazie Enzo.
caro Guido,
aggiungo, in modo banale, la tua figura nel caso di una massa perfettamente simmetrica... E' una sciocchezza, ma è meglio non dare niente per scontato (pensiamo a tutti i lettori...)
Ciao Enzo, nella fig. 3, si suppone una cabina in caduta libera immersa in un campo gravitazionale, pertanto il raggio di fotoni sarà visto parallelo al pavimento dall’interno della cabina e come ramo di parabola visto dall’esterno, esatto?
esattamente il contrario... chi è dentro la vede entrare in un punto e la vede uscire da un punto che non è sulla stessa linea orizzontale del primo.
Forse ho dimenticato di dire che supponevo che nella fig. 3 la sorgente del raggio di fotoni fosse interna alla cabina che cadendo di moto accelerato uniforme si può localmente considerare un sistema inerziale. Pertanto al suo interno il passeggero, non percependo nessun moto, deve vedere il raggio parallelo al pavimento, mentre dall'esterno si vede cadere il raggio su un ramo parabolico. Viceversa a se il raggio proviene da fuori e attraversa la cabina che cade, il passeggero lo vedrà salire localmente verso l'alto sempre su ramo parabolico, mentre dall'esterno sarà visto proseguire su l'apparente retta della geodetica propria del campo gravitazionale specifico. Così va bene?
molto meglio !