Riproponiamo, diviso in sei puntate, un articolo che deve rappresentare l'ABC per chi volge lo sguardo al cielo: una semplice spiegazione di come funziona quella stupefacente macchina del tempo che l'Universo mette a disposizione di chiunque abbia occhi e testa (e un pizzico di buona volontà!) per comprenderla ed ammirarla. Questa terza puntata è dedicata al concetto di Universo Osservabile.

QUI le altre puntate  -  QUI l'articolo intero (pubblicato il 10/1/2018)

 

L'Universo Osservabile  (senza espansione)

Ne abbiamo già accennato precedentemente, ma penso valga la pena, per molti dei meno esperti, riassumere le idee in modo estremamente divulgativo. Perfino i nostri amici Astericcio & co. hanno fatto la sua conoscenza, attraverso un colloquio che sembrerebbe del tutto estraneo all’argomento.

Innanzitutto, un paio di premesse. Qualsiasi grafico o schema che rappresenti l’evoluzione dell’Universo contiene degli errori. D’altra parte è impossibile descrivere su un foglio un qualcosa che rappresenti le quattro dimensioni, di cui una, il tempo, è anche estremamente particolare.

Pur accettando una semplificazione che rasenta il limite della realtà dei fatti, è estremamente importante capire sempre che il suo valore è soltanto indicativo, a grandi linee. Guai a considerare realistica qualsiasi rappresentazione vi venga data. Una per tutte, il palloncino che si gonfia.

Essa rappresenta un modo estremamente sintetico e immediato per comprendere l’espansione dell’Universo e la crescita continua delle distanze tra i corpi che lo abitano. Ma, non cerchiamo assolutamente un collegamento diretto e semplice con la curvatura dello spaziotempo, di cui si sente parlare spesso e volentieri. Sono due cose estremamente diverse! L’espansione vede, nella superficie sferica che si allarga sempre più, un’ottima rappresentazione fino a un certo livello, permettendo di comprendere alcuni concetti essenziali come appunto l’Universo Osservabile.

La curvatura dello spaziotempo è invece qualcosa che ha bisogno della relatività generale di Einstein, in quanto racconta l’immane lotta tra espansione e gravità. Essa porta alla definizione di “forma” dell’Universo, concetto del tutto estraneo alla forma che intendiamo noi. La forma di una scatola o di una persona ci dice come la massa sia sistemata entro certi confini, mentre la forma dell’Universo ci dice “solo” che tipo di geometria può essere usato per descriverlo. In questo senso è pericolosissimo pensare al palloncino che si gonfia come a una visione della curvatura dello spaziotempo. Per il nostro livello, sono concetti del tutto estranei tra di loro, che potrebbero unificarsi solo attraverso trattazioni ben più complesse. Non diciamo altro per non confondere le idee, ma cerchiamo di ricordare sempre di non prendere le rappresentazioni divulgative come “oro colato”.

Bene, fatte queste dovute premesse, occupiamoci del concetto di Universo Osservabile, un vero e proprio limite della nostra conoscenza attuale, impostoci dall’espansione dell’Universo, ma che esisterebbe comunque anche per un Universo statico, che sia da sempre stato come è oggi. La sua limitatezza dipende sempre e soltanto dalla velocità della luce, molto alta per noi, ma non per le distanze dell’Universo.

Iniziamo con questa seconda ipotesi (attenzione che non sono molti anni che è stata scartata… lo stesso Einstein c’aveva creduto).

Immaginiamo che l’Universo sia nato, improvvisamente, 13.7 miliardi di anni fa. Nato già bello che costruito come teatro di sfondo, al cui interno si sono formati gli attori come le particelle elementari, gli atomi, le molecole, le stelle, le galassie e tutto ciò che volete, in tempi relativamente brevi. Qualcosa di simile alla descrizione della pioggia fatta precedentemente.

Il suo enorme vantaggio è che due stelle nate a una certa distanza una dall’altra mantengono sempre la stessa distanza al passare del tempo. Non parliamo di variazioni di distanza locale, dovute a mutue interazioni gravitazionali, ma alla distanza legata alla crescita dell’Universo. Facciamo molto prima a disegnare la Fig. 9.

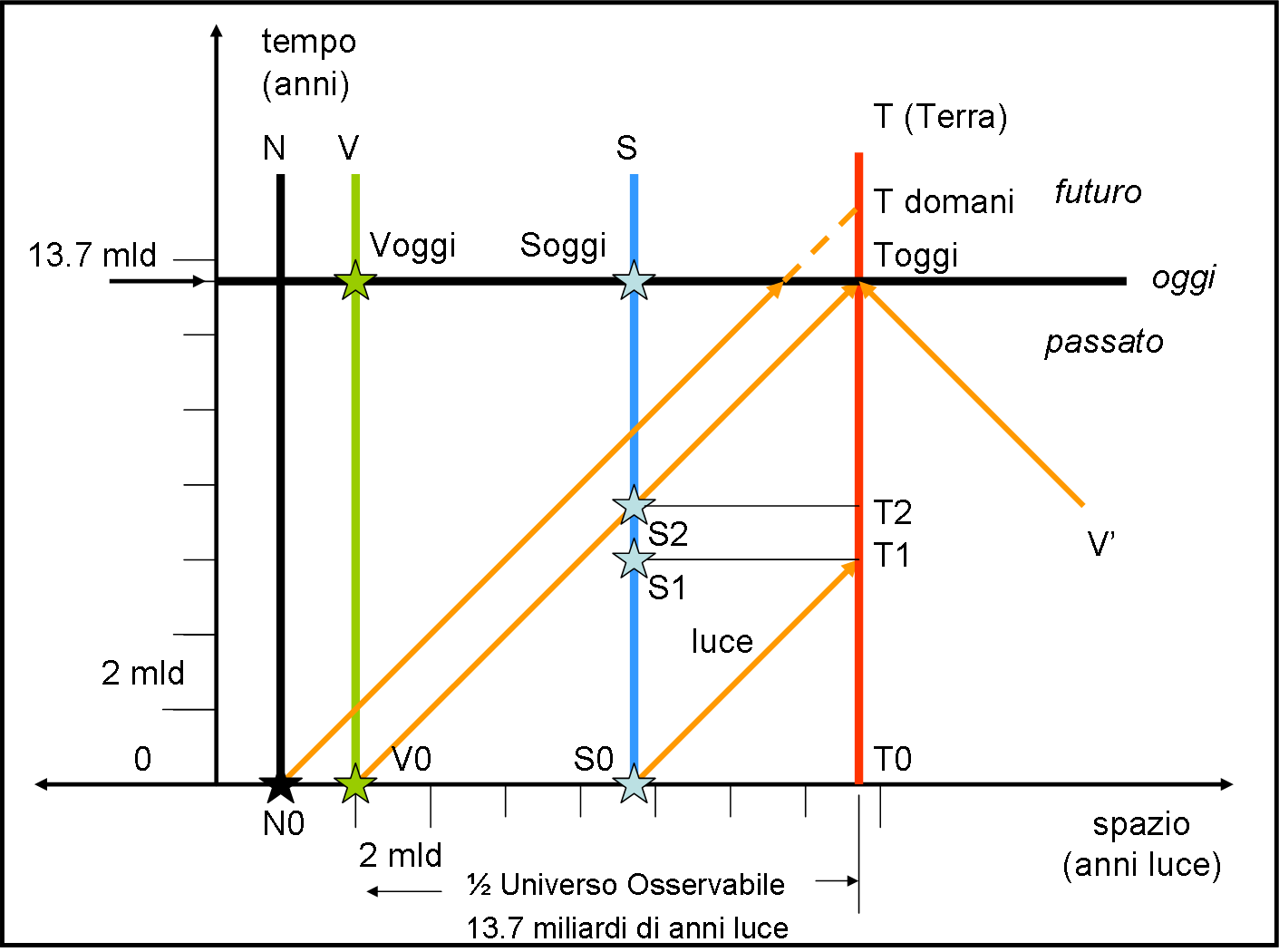
La linea della ascisse (x) è lo spazio (tre dimensioni trasportate in una sola, ricordiamocelo bene, come farlo lo abbiamo spiegato QUI alla figura 6), quella delle ordinate (y) è il tempo che scorre. Quale unità di misura prendiamo? Beh… qualcosa che aiuti a descrivere il movimento della luce, l’unico tipo di informazione che ci proviene dall’Universo (per luce si intende qualsiasi tipo di radiazione elettromagnetica, sia luce visibile, che raggi X, raggi gamma, e onde radio). O, meglio, anche se non è più l'unica informazione che ci arriva (come abbiamo raccontato QUI) è senza dubbio quella che, dato l'attuale livello della nostra tecnologia, è più facile analizzare ed interpretare.

Consideriamo, quindi, la luce l’unica informazione che una stella può mandare a un’altra stella (o pianeta o quello che volete), con i suoi pregi e i suoi limiti.

All’istante t = 0 nasce l’Universo e possiamo anche dire che nascono le varie stelle S,V,N, ecc., anche se ci vuole un po’ di tempo prima che un ammasso di idrogeno diventi una vera stella. Tuttavia, l’approssimazione ha poca importanza per il nostro discorso. Al posto della stella Sole, mettiamo direttamente la Terra T (per la scala del Cosmo, coincidono perfettamente). Abbiamo messo la Terra più o meno al centro del grafico solo per motivi egoistici, ma ricordiamoci che l’Universo non ha un centro! Qualsiasi stella può benissimo e giustamente considerarsi al centro. E ricordiamoci che l'aveva intuito perfettamente già il grandissimo Giordano Bruno.

Ciò che conta sono le distanze relative e non le distanze rispetto a una qualsiasi origine che non esiste. In una figura del genere non esiste Big Bang, ma lo spazio-tempo nasce tutt’assieme (o è sempre esistito in un’altra forma senza emissione di luce), e poi rimane quello che è, senza espandersi. Il Big Bang può essere considerato, perciò, la retta delle ascisse, al tempo t = 0.

Torniamo alle unità di misura. Lo spazio unitario può essere considerato quello percorso dalla luce in un certo intervallo di tempo (spazio misurato in anni luce). Quello delle ordinate proprio questo intervallo di tempo (tempo misurato in anni).

Ammettiamo, per esempio, di mettere una tacchetta nell’asse delle x a ogni intervallo di spazio corrispondente a quello percorso dalla luce in due miliardi di anni (è facilissimo trasformarlo in chilometri, ma avremmo un po’ troppe cifre da scrivere…). Le tacche dell’asse del tempo sarebbero intervallate proprio da due miliardi di anni. Come si muove la luce in questo semplice diagramma? Beh… è veramente banale. Essa percorre un intervallo unitario delle x (due miliardi di anni luce) proprio in un intervallo di tempo unitario (due miliardi di anni). In poche parole, essa descrive una retta inclinata di 45 gradi rispetto agli assi x e y, in modo che ogni suo punto abbia sempre l’ordinata y uguale all’ascissa x, ossia la retta y = x.

L’asse delle y non è, però, infinito. Esso si ferma al punto OGGI, un punto che corrisponde a 13.7 miliardi di anni, ossia all’età dell’Universo (come lo pensiamo noi)! Invece l’asse delle x può essere anche infinito, dato che non sappiamo quanto sia esteso l’Universo (le cui “dimensioni”, però, restano sempre uguali).

In questo diagramma, le stelle non si muovono nello spazio, ma solo nel tempo e, quindi, descrivono rette parallele tra di loro e all’asse del tempo (perpendicolari all’asse dello spazio). le possiamo chiamare linee di Universo.

Consideriamo una stella S che invii la sua luce nell’Universo all’istante t₀. La luce si muove secondo una retta inclinata di 45° e raggiunge la Terra in T₁. In quel momento la Terra vede la stella, ma la vede com’era al tempo in cui è partita la sua prima luce, ossia al tempo t = 0.

Nel frattempo, però, la stella si è mossa nel tempo ed è già arrivata in S₁. La distanza tra T₁ e S₁ (distanza al momento dell’arrivo della luce) rimane invariata ed è uguale a T₀S₀ (distanza al momento della partenza della luce).

Come abbiamo detto l’Universo non si espande e le stelle non si muovono: la loro distanza rimane la stessa in ogni istante. Tuttavia, a causa della lentezza della luce, noi vediamo in T₁ la luce partita da S₀ e non certo quella che sta inviando da S₁. In S₁ la stella potrebbe anche non esistere più, ma io la vedrei comunque all’istante in cui T raggiunge T₁, dato che sto ancora guardando la luce-informazione partita quando era appena nata, ossia quando era in S₀.

Portiamoci adesso al tempo T_oggi. Se esistesse ancora, vedremmo la stella S com’era nel momento in cui ha “sparato” la luce che arriva oggi. Ossia vedremmo la stella com’era in S₂, quando la Terra era ancora in T₂. La luce impiega del tempo per percorrere la distanza S₂T₂ = S₀T₀ = S₁T₁ e colpisce la Terra solo oggi.

Ripetiamo: oggi vediamo la luce della stella, inviata quando era in T₂. Tuttavia, oggi, la stella S ha continuato a muoversi nel tempo e quindi la sua posizione attuale è S_oggi. Poco male, la distanza effettiva tra la Terra T_oggi e la stella S_oggi è sempre la stessa ed è uguale a S₀T₀, com’era all’inizio dell’Universo. Come sarebbe bello se fosse veramente così…

Tuttavia, siamo interessati a scoprire la stella, osservabile oggi, più lontana possibile, quella che determina una specie di siepe oltre alla quale non si può vedere niente. Quale sarà? Semplice… quella la cui luce inviata al tempo t = 0 (ossia la sua prima luce) arriva solo oggi.

E’ facile trovarla, basta mandare indietro la luce fino a che incontri l’asse dello spazio, ossia fino all’istante t = 0. Questa stella è, quindi, V. Ripetiamo: la sua prima luce ci arriva solo oggi. Una stella più lontana, come N, non riusciamo ancora a vederla, dato che la sua luce ci raggiungerà solo domani, come indica la linea tratteggiata. Essa fa parte di ciò che esiste, ma sta oltre la siepe. E’ un attrice dell’Universo, ma un’attrice che non conosciamo ancora. La conosceremo solo domani, com’era, però, al momento in cui mandava i suoi primi vagiti.

Facciamo un piccolo calcolo. Quanto tempo è passato da quando la luce di V è partita? Presto detto: esattamente 13.7 miliardi di anni, l’età dell’Universo. La linea percorsa dalla luce viaggia a 45°, ne segue, quindi, che la distanza V₀T₀  è uguale a 13.7 miliardi di anni luce. Ricordiamo sempre che le distanze si misurano lungo le linee orizzontali, mentre il tempo lungo quelle verticali, La linea spaziotemporale della luce inclinata a 45° ci dice solo che un certo numero di anni luce (distanza) viene coperta nello stesso  numero di anni (tempo).

Dove si trova adesso la stella V? Esattamente in V_oggi (anche lei viaggia solo nel tempo come la Terra). La distanza V_oggiT_oggi è però uguale a V₀T₀.

In ogni modo, malgrado l'estrema semplicità, chiamiamo Universo Osservabile il doppio della distanza V_oggiT_oggi. Perché il doppio? Perché ci sarà una stella dall’altra parte della Terra che farà la stessa cosa e quindi lo spazio contenente tutte le stelle che siamo riusciti a vedere fino a oggi deve essere uguale da una parte e dall’altra, e, quindi, l’Universo Osservabile è proprio il doppio di V_oggiT_oggi = V₀T₀.

In altre parole, l’Universo Osservabile indica la posizione odierna di tutto ciò la cui luce ci sta raggiungendo oggi. Ovviamente, la luce può provenire sia da oggetti vicini (la loro prima luce ci ha raggiunto per la prima volta molto tempo fa) sia da oggetti lontanissimi (la loro prima luce ci raggiunge oggi per la prima volta). Esso è limitato, in quanto non contiene “ancora” i corpi celesti la cui prima luce non ci ha ancora raggiunto. E, perciò, ben diverso dall’intero Universo che potrebbe essere enormemente più grande, ma di cui non abbiamo ottenuto informazione alcuna (e potrebbe darsi che mai l’otterremo).

Vale la pena spiegare meglio questo concetto, spesso male interpretato… Lo facciamo per un Universo statico e lo rifaremo per un Universo in espansione. Ci aiuta la Fig. 10.

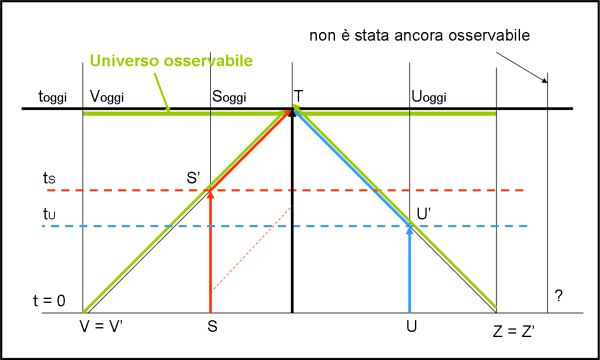
Quali sono le stelle la cui luce ci raggiunge oggi? Beh… la luce deve giungere a noi in modo da formare un angolo di 45° con la direzione del tempo. Così deve fare quando parte e così deve fare quando arriva (è come se partissimo da oggi e seguissimo, indietro nel tempo, la luce che ci sta raggiungendo).

Consideriamo la stella S che si muove, come tutte, in senso verticale. La sua luce ci ha già raggiunto nel passato (come mostra la linea diagonale rossa a trattini), ma a noi interessa quella che ci raggiunge OGGI. Per cui, tracciamo da oggi la linea a 45° fino a incontrare la linea di Universo della stella S in S’. La luce della stella S che riceviamo OGGI è quella partita da S’ al tempo t_s. In altre parole, la stella S che vediamo oggi è quella che apparteneva all’Universo tratteggiato in rosso, relativo al tempo t_s. Dove si trova la stella S, OGGI? Presto detto in S_oggi, dato che deve appartenere all’Universo di oggi. Cosa analoga capita alla stella U. Oggi riceviamo la luce che ha inviato quand’era in U’, al tempo t_U, nell’Universo relativo a quel tempo. Particolare importanza ha la stella V e  sua “sorella” Z. Anche la loro luce arriva OGGI, ma è partita proprio all’inizio del tempo, quando t = 0.

Ne deriva che la luce delle stelle più lontane di V e Z , all’origine dei tempi, NON può ancora essere arrivata fino a noi. Lo farà domani o dopodomani o tra un miliardo di anni, ma per adesso NON E’ ANCORA STATA OSSERVABILE.

L’Universo Osservabile OGGI ha, perciò, come confini le posizioni delle stelle Z_oggi e V_oggi e contiene tutte le stelle più vicine (osservate per la prima volta in tempi diversi), nella posizione che hanno OGGI (U_oggi e S_oggi). L’Universo Osservabile di OGGI è, infatti, la linea orizzontale che passa per T, di cui l’Universo osservabile è il suo tratto verde.

Riassumendo: noi oggi riceviamo la luce di stelle partita in tempi diversi. La loro posizione attuale costituisce l’Universo Osservabile. Come vedete, in queste definizioni si parla di arrivo della luce, non di sua rilevazione. I nostri telescopi potrebbero non essere in grado di  “vedere” qualcosa, anche se teoricamente la luce è arrivata. Non confondiamo, quindi, Universo Osservato realmente (e posizione attuale delle stelle osservate), dipendente dai nostri limiti tecnologici, con Universo Osservabile che dipende solo dalla velocità della luce.

Finora, le distanze tra le stelle si sono mantenute costanti, facilitando la comprensione. Tuttavia, la situazione è già stata sufficiente per la definizione di Universo Osservabile.

Essa è anche sufficiente per un’altra definizione, quella di Cono di Luce. Esso non è altro che il triangolo formato dalle linee della luce VT_oggi e ZT_oggi ed è identificato dalle linee di luce degli oggetti che ci raggiungono oggi. Al suo interno sono contenute tutte le linee di luce delle stelle già osservabili in tempi passati. Le stelle, le cui linee di Universo sono sempre state esterne a questo triangolo di luce, non fanno ancora parte del nostro Universo Osservabile odierno.

In poche parole, il Cono di Luce rappresenta il nostro passato con le uniche informazioni (luminose, ma non solo) ricevute dall’Universo. Noi non possiamo vedere l’Universo Osservabile come è OGGI, ma possiamo vedere le stelle che lo compongono come erano in tempi diversi (antichissimi per le più lontane e  recentissimi per le più vicine). Un esempio? La galassia di Andromeda la vediamo com’era circa due milioni e mezzo di anni fa, mentre il Sole lo vediamo com’era otto minuti fa!

Da come è stato costruito, ogni stella dell’Universo ha un suo Universo Osservabile, diverso dal nostro o parzialmente o completamente. Ce lo mostra la Fig. 11.

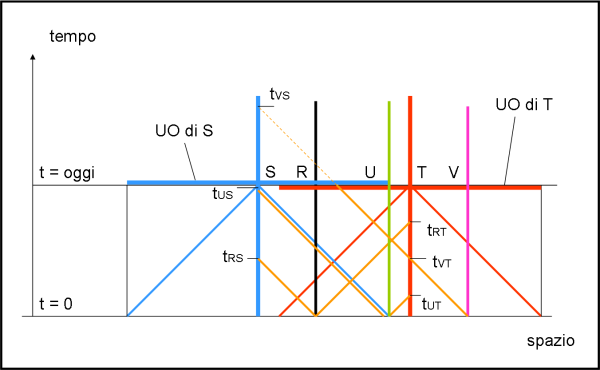
Consideriamo la Terra T e la stella S, con le loro linee di Universo rossa e blu, rispettivamente. Al tempo OGGI, esse hanno i loro Universi osservabili, descritti dalle linee orizzontali rosse e blu. Si vede bene come essi abbiano solo una parte in comune. Facciamo qualche semplice esempio.

La stella R (nera) invia la sua prima luce sia a sinistra che a destra. Essa raggiunge la Terra al tempo t_RT e la stella S al tempo t_RS , ben prima di oggi._. Essa, quindi, appartiene all’Universo Osservabile odierno sia di S che di T. D’altra parte si vede bene che oggi la stella R appartiene sia al tratto orizzontale rosso che a quello blu. Potete controllare da soli, come piccolo esercizio, che la stella U (verde) appartiene anch’essa a entrambi gli Universi osservabili (anche se è al limite di quello di S: la prima luce di U raggiunge S solo oggi). Ben diversa è la situazione della stella V (viola), che appartiene all’Universo osservabile di T, ma non a quello di S. Ne farà parte solo nel futuro, al tempo t_VS.

Dalle figure precedenti possiamo notare che tutte le stelle visibili oggi dalla Terra, sono relative a posizioni che stanno lungo le rette della luce che individuano l’Universo osservabile. Sembrerebbe vederle tutte nella stessa direzione… Non commettete questo errore! Noi abbiamo considerato lo spazio a una dimensione. Basterebbe considerare un piano (due dimensioni) e avremmo un cono descritto dalle linee della luce e non più un triangolo (da cui il nome), come mostra la Fig. 12.

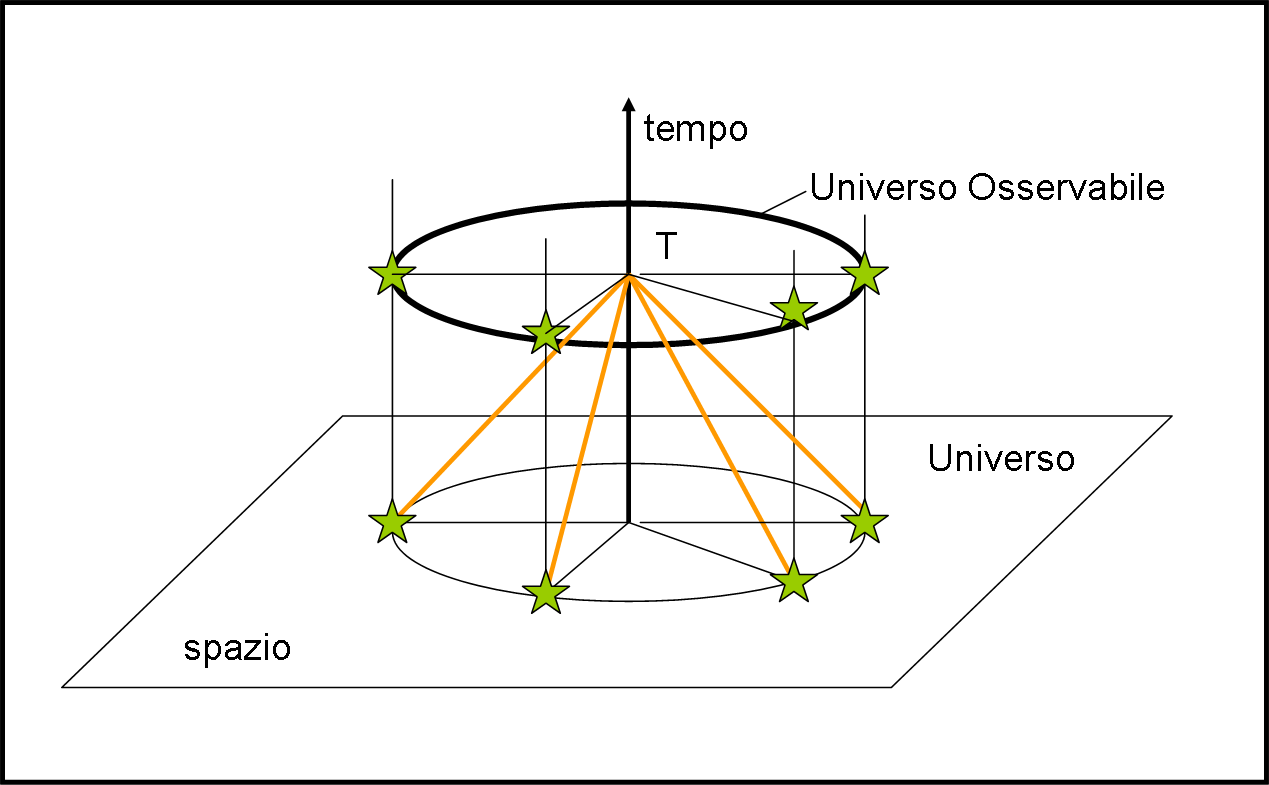
Ci manca ancora una dimensione spaziale, ma non possiamo proprio disegnarla… E questo comporta la necessità di limitarci a una o al massimo due dimensioni spaziali. Il vero Universo avrebbe bisogno di una figura ben più complicata… ma irrealizzabile.

Notiamo anche che l’Universo Osservabile di oggi è più piccolo di quello di domani e più grande di quello di ieri. E’ facile mostrare come varia l’Universo Osservabile di T al passare del tempo, come mostrato in Fig. 13 (costruitevela da soli, come esercizio).

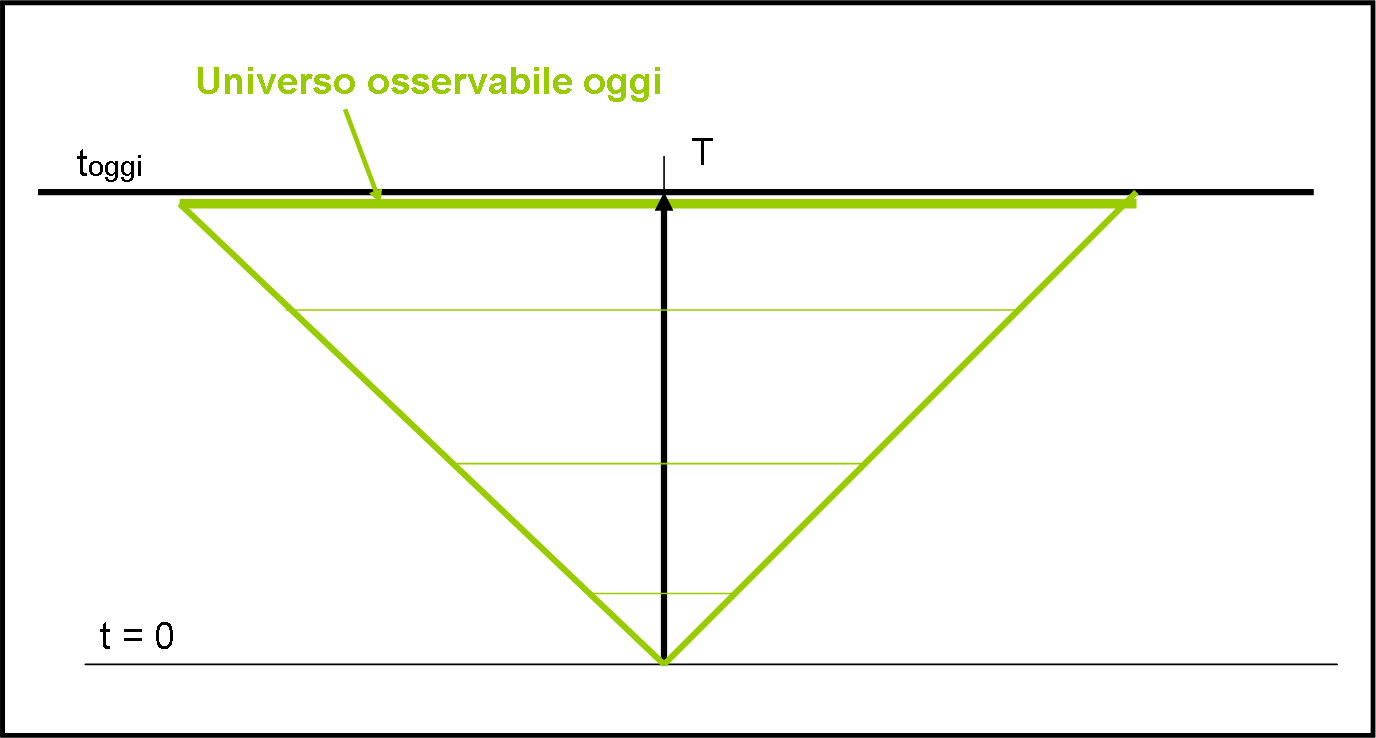
In ogni modo, potete verificare che, in questo caso semplificato in cui abbiamo ipotizzato un universo statico e non espansione, l’Universo Osservabile è sempre uguale allo spazio percorso dalla luce negli anni trascorsi dalla nascita dell’Universo.

Le cose diventano più complicate, ma non poi tanto, considerando un Universo in espansione.

Attenzione! Talvolta può accadere di vedere una figura simile alla Fig. 9 anche con l’Universo in espansione. Ciò si riesce a realizzare conoscendo di quanto si espande l’Universo (in media) e cambiando coordinate in modo che essere rimangano sempre uguali. Stiamo parlando di coordinate comoventi. Ma, questo tipo di rappresentazione comporta passaggi più complessi e meno intuitivi per cui non lo tratteremo (almeno per adesso).

 

Continua...

QUI le altre puntate  -  QUI l'articolo intero (pubblicato il 10/1/2018)