Categorie: Matematica
Tags: angoli esterni poligono area esagono geometria lati para lati paralleli a due a due quiz soluzione teorema dei seni teorema del coseno
Scritto da: Vincenzo Zappalà
Commenti:6
Soluzione dell'area di un esagono "strambo" ***
Innanzitutto, un "bravissimo" ad Andy che ha descritto, nei commenti, una perfetta soluzione del quiz sull'esagono. In questo articolo do un procedimento leggermente diverso, che dimostra come la matematica (e la geometria) non abbia regole così ferree come molti credono. Lascia sempre il "libero arbitrio". l'importante è che la conclusione sia unica.
Il problema sarebbe facilmente risolvibile se conoscessimo anche il lato dell'esagono. Chiamiamolo x e vediamo la Fig. 1:

Scegliamo un punto O, interno all'esagono, qualsiasi e uniamolo con dei segmenti ai vertici dell'esagono. Otteniamo 6 triangoli diversi tra loro. Consideriamo, dapprima, i due triangoli rosa. Essi hanno x come base e h e k come altezze rispettive. Ne segue che le loro aree sono date da:
Ar1 = x h/2
e
Ar2 = x k/2
La somma delle due aree è quindi:
Ar1 + Ar2 = x h/2 + x k/2 = x (h + k)/2
Ma (h + k) non è altri che la distanza tra le due basi dei triangoli, ossia 237:
Ar1 + Ar2 = 237 (x/2)
Procedimento analogo possiamo seguire per i due triangoli verdi e i due azzurri, da cui segue:
Av1 + Av2 = 192 (x/2)
Aa1 + Aa2 = 195 (x/2)
La somma dei sei triangoli è proprio l'area dell'esagono e quindi:
AESA = Ar1 + Ar2 + Av1 + Av2 + Aa1 + Aa2
AESA = (237 + 192 + 195)(x/2)
AESA = 312 x .... (1)
Purtroppo, però, non conosciamo x e quindi il vero problema sta nel ricavarlo in base ai dati di partenza.
Lasciamo da parte la (1), che ci servirà alla fine, e disegniamo nuovamente l'esagono in Fig. 2.

Prolunghiamo i lati dell'esagono e tracciamo le tre rette rosse (m, n e p), passanti per i vertici F, E e D, rispettivamente, e perpendicolari alle tre distanza, conosciute, tra i lati paralleli dell'esagono. Individuiamo tre coppie di triangoli (azzurri, rosa e verdi). Cominciamo con i due triangoli azzurri: essi sono entrambi rettangoli, hanno l'ipotenusa (lato x dell'esagono) uguale così come un angolo, perché opposto al vertice. Ne segue che i due triangoli sono congruenti.
Chiamiamo a il loro cateto maggiore
Discorso analogo vale per i due triangoli azzurri (attenzione: essi NON sono congruenti con quelli rosa), che sono anch'essi congruenti.
Chiamiamo b il loro cateto maggiore
Ripetiamo nuovamente lo stesso discorso per i due triangoli verdi e chiamiamo c il loro cateto minore.
Risulta immediato che
a + b = 237
b + c = 192
c + a = 195
Abbiamo un banale sistema di tre equazioni in tre incognite (a, b e c) che si risolve facilmente. Ad esempio, possiamo sommare le tre equazione e ottenere:
2 (a + b + c) = 624
a + b + c = 312 (risultato che non ci sorprende affatto, avendo nuovamente sommato le tre distanza note e diviso il risultato per 2, come fatto nella (1))
c = 312 - (a + b) = 312 - 237 = 75
b = 192 - 75 = 117
a = 237 - 117 = 120
Riassumendo:
a = 120
b = 117
c = 75
A questo punto, potremmo anche dedurre interessanti conclusioni sul fatto che l'area dell'esagono risulta uguale a quella di tre rettangoli di lati a e x, b e x e c e x (AESA = ax + bx + cx), ma resta il fatto che non conosciamo x e quindi dobbiamo, comunque, ricavarlo.
Consideriamo, allora. la Fig. 3, in cui si sono evidenziati gli angoli esterni all'esagono, ossia quelli che il prolungamento di un lato fa con il lato successivo. In poche parole, i due angoli azzurri, i due rossi e i due verdi.

Chiamiamoli con il nome del vertice (A ed E, B ed F, C e D).
Sappiamo che la somma degli angoli esterni di un poligono qualsiasi è uguale all'angolo giro, ossia a 360°. Posiamo perciò scrivere che:
A + B + C + D + E + F = 360°
Ma, essendo i lati paralleli a due a due, segue immediatamente che:
A = E, B = F, C = D
2A + 2B + 2C = 360°
A + B + C = 180° .... (2)
Dai triangoli colorati, possiamo, però, anche scrivere:
x sen (A) = a
x sen (B) = b
x sen(C) = c
ossia:
x = a/sen(A)
x = b/sen(B)
x = c/sen(B)
a/sen(A) = b/sen(B) = c/sen(C) .... (3)
La (2) ci dice che gli angoli A, B e C sono gli angoli di un triangolo, ma la (3), che non è altro che il teorema dei seni, ci dice anche che i lati del triangolo devono essere a, b e c (Fig. 4).

Non ci resta, allora, che scrivere il teorema del coseno per questo triangolo:
a2 = b2 + c2 - 2bc cos(A)
e ricavare cos(A)
cos(A) = (b2 + c2 - a2 )/(2bc) = (7/251172 + 752 - 1202)/(2 · 117 · 75) = 7/25
ma sappiamo anche che:
sen(A) = √(1 - cos2(A)) = √1 - (7/25)2 = 24/25
Sapendo che:
x = a/sen(A)
si ottiene finalmente x:
x = 120/(24/25) = 25 120/24
x = 125
Questo valore può essere inserito nella (1), ottenendo l'area dell'esagono:
AESA = 312 · 125 = 39 000
Il quiz lo trovate QUI






6 commenti
Caro Enzo,
come appendice al problema, è possibile ottenere una formuletta generale nel caso di un esagono equilatero convesso (equilatero non significa strettamente anche equiangolo, come dimostra il problema proposto);
una volta trovate le misure (a, b, c) attraverso le quali si dividono le tre altezze, misure che poi comporranno il triangolino di figura 4, l'area dell'esagono si può esprimere in funzione solamente di a, b, c, come:
"semiperimetro del triangolino moltiplicato per il prodotto dei sui lati, diviso la sua area"
in formula: Areaesagono =(s-b)(s-c)}&space;})
nel caso proposto: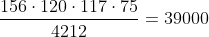
Nel caso di un esagono regolare (equilatero ed equiangolo), le altezze sono tutte e tre uguali a pari a 2 volte l'apotema, le stesse altezze si dividono in due parti uguali, per cui si avrà:
a = b = c = apotema dell'esagono
e il triangolino di figura 4 sarà allora un triangolo equilatero di lato pari all'apotema dell'esagono stesso, e
applicando la formuletta: Areaesagono =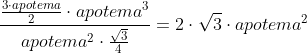
ma l'apotema dell'esagono è pari a: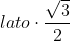 ed elevando al quadrato:
ed elevando al quadrato: 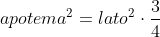
sostituendo nella precedente: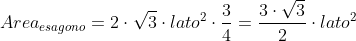
che dovrebbe confermare la validità della formuletta generale.
ottimo Andy... se sei d'accordo metterei il tuo ragionamento nell'articolo di soluzione, magari aggiungendo un paio di figure. Dimmi anche tu se hai idee per renderlo ancora più semplice e immediato. Sei un grande collaboratore! Grazie infinite
Certamente Enzo, grazie a te!!
perfetto!
È anche possibile calcolare l'area dell'esagono direttamente dalle sue altezze:
io le ho denominate g, h, i con g > h > i (237 > 195 > 192)
che producono i segmenti a, b, c con a > b > c (120 > 117 > 75).
Questa è la formula generale:
qui la dimostrazione: https://i.imgur.com/1cLwmSR.png
di seguito l'esempio numerico
bravo Andy! Metti tutto insieme e facciamo una corposa aggiunta!