Questo è il quinto articolo della serie "La Relatività Generale al microscopio"

Uno dei punti essenziali di tutta la teoria della relatività generale è l'indipendenza dei risultati dal sistema di riferimento scelto, qualcosa di simile a quanto ottenuto dalla relatività galileiana e ristretta. Possono cambiare le coordinate, ma non il valore di un certo evento o, meglio, del campo a lui associato. In sintesi: ciò che è vero in un sistema di riferimento deve essere vero in tutti i sistemi di riferimento.

Per potere essere sicuri di ottenere questa indipendenza è, quindi, necessario sapere bene come passare da un sistema a un altro.  Cominciamo dalle coordinate di un punto-evento P. Se esse sono xⁿ, in un sistema , quanto valgono in un qualsiasi altro sistema?  Teniamo anche ben presente che vale sempre e comunque la relatività ristretta e che i sistemi di coordinate cambiano in modo ormai ben noto, quando vi è un sistema in moto rispetto a un altro.

Vediamo, allora, come fare per collegare tra loro le coordinate di un certo punto-evento, in due sistemi di riferimento diversi. In particolare, vediamo come sia possibile trasformare i gradienti calcolati in un certo sistema di riferimento nei gradienti calcolati in un altro sistema di riferimento.

Iniziamo considerando, per semplicità figurativa, n = 2

Abbiamo il "vecchio" sistema x¹ e x² e introduciamo il nuovo sistema di coordinate y¹ e y². Notiamo subito una cosa:  la nuova coordinata y¹ può essere espressa, in coordinate x¹ e x² del vecchio sistema come mostrato nella Fig. 8.

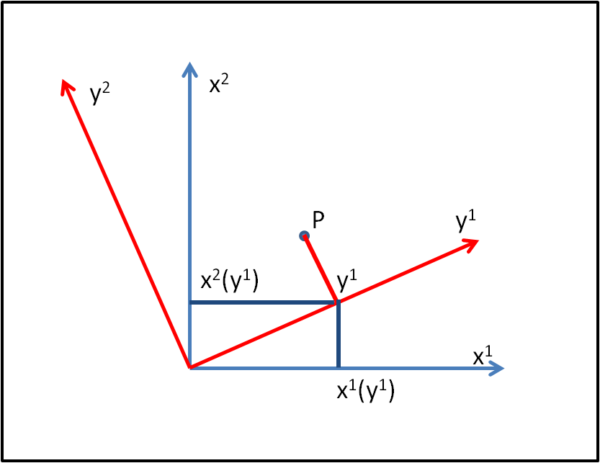
In parole semplici, possiamo dire che i valori x¹ e x² del vecchio sistema dipendono dal valore di y¹, ossia sono una sua funzione. In altre parole, dato un y¹ ne conseguono subito i valori x¹ e x² corrispondenti.

Attenzione: ricordiamo ancora che y non è più l'ordinata di un punto, ma una qualsiasi coordinata di un altro sistema. Mi raccomando, digeriamo bene questo concetto!

Ammettiamo di conoscere i gradienti nel punto P del vecchio sistema, ∂Φ/∂x¹ e ∂Φ/∂x², come possiamo scrivere il gradiente  ∂Φ/∂y¹ ? Non è difficile, ricordando che x¹ e x² sono entrambi funzione di y¹: basta ricordare la derivata di funzione di funzione (derivate parziali in questo caso):

∂Φ/∂y¹ = (∂Φ/∂x¹)(∂x¹/∂y¹) + (∂Φ/∂x²)(∂x²/∂y¹)

Ovviamente, abbiamo tenuto conto  delle due componenti x¹ e x² di y¹

La formula precedente va intesa molto bene. Il tutto si riferisce al gradiente relativo alla sola coordinata y¹, ma è necessario introdurre due derivate parziali relative a x¹ e x².

Possiamo facilmente estendere la formula da due a tutte le m coordinate del sistema x^m  (abbiamo usato m al posto di n, ma poco cambia dato che esso è solo l'indice che indica quale asse si considera ed è sempre legato a una sommatoria) e otteniamo:

∂Φ/∂y¹ = ∑_m(∂Φ/∂x^m)(∂x^m/∂y¹)

E ripetere l'espressione per ogni coordinata yⁿ (dove anche n può essere un numero qualsiasi e non più due)

∂Φ/∂yⁿ = ∑_m(∂Φ/∂x^m)(∂x^m/∂yⁿ)                  .... (2)

Essa fornisce i nuovi valori dei gradienti in un qualsiasi sistema di riferimento, noti quelli in un sistema di riferimento iniziale

Nota Bene: Stiamo mettendo in evidenza alcune formule che vengono "costruite" nel modo più semplice possibile. Tuttavia, facciamole nostre e capiamole molto bene, dato che nel proseguo della trattazione verranno sicuramente richiamate e prese come assodate una volta per tutte. Non potremo certo, ogni volta che si richiamano, rispiegarle nuovamente... Questo è uno dei grandi problemi legati a equazioni estremamente  articolate come quelle di Einstein.

Andiamo, perciò, avanti molto lentamente...