Mettiamoci alla prova - Gradienti e Trasformazioni di Coordinate

11/12/20

Mettiamoci alla prova - Gradienti e Trasformazioni di Coordinate

Categorie: Relatività Tags: Scritto da: Fabrizio Commenti:6

Questo articolo fa parte della sezione "METTIAMOCI ALLA PROVA!" all'nterno della Relatività Generale al microscopio

 

Seguendo gli articoli di Enzo della serie La Relatività Generale al microscopio ho cercato di mettermi alla prova applicando le nozioni illustrate a qualche caso particolare. Ho pensato che poteva essere interessante anche per altri frequentatori del circolo confrontarsi con queste applicazioni e utile per me confrontarmi con le loro soluzioni.

In questo articolo trovate alcuni casi relativi al quinto articolo, quello sulle trasformazioni di coordinate.

In fondo riporto l'esito che ho ottenuto dai calcoli richiesti in alcune domande in modo che possiate confrontarli con i vostri. Non garantisco che i miei risultati siano corretti. Per il momento non riporto il processo seguito, che è il vero scopo della domanda.

Il caso che ho pensato è questo.

In questo grafico i valori  della funzione F sono stati rappresentati dei colori secondo la corrispondenza indicata nella barra a destra. Punti dello stesso colore hanno valori uguali.

Nel grafico sono anche tracciate le linee coordinate delle coordinate polari che usiamo come riferimento. Per chi volesse avere maggiori dettagli sulle coordinate polari li può trovare in questo articolo.

Ora veniamo alle domande.

 

Esito dei calcoli (il testo è nascosto, si vede selezionando la riga)

Domanda 2:   [-2r,0]

Domanda 4: [-2x,-2y]

Domanda 6: [-1,0]

 

Articoli correlati

6 commenti

  1. Fabrizio
    11/12/2020 at 22:12

    Ho modificato la domanda 4 che nella versione precedente era una ripetizione della 2.

  2. Arturo Lorenzo
    15/12/2020 at 11:55

    Comincio dalla domanda 2

    Le espressioni delle due componenti del gradiente nelle coordinate polari date sono :

    \frac{\partial F}{\partial r}=-2r

    \frac{\partial F}{\partial \varphi }=0

    Quindi, rispondendo ora alla domanda 1, la componente costante è quello secondo l'angolo \varphi ed è pari a zero. Cio' si evince anche visivamente guardando il primo grafico. Si nota, infatti, che posizionandoci ad una certa distanza r dall'origine, girando attorno all'origine lungo una circonferenza di raggio r, il colore resta costante. Forse la circostanza sarebbe ancora più evidente con una rappresentazione della funzione z=F(r, \varphi) nello spazio r, \varphi, z

    Sempre se ho capito bene.

    (ieri ho smanettato anche con le restanti domande, ma ora sono in ufficio e ho già scritto troppo.. :-D )

     

  3. Arturo Lorenzo
    15/12/2020 at 16:38

    Sono sempre in ufficio, ma posso permettermi un'altra distrazione :lol:

    Domanda 3: entrambe le componenti del gradiente sono nulle in un solo punto, ossia nell'origine. Infatti, solo nell'origine , spostandoci di una quantità infinitesimale lungo x oppure lungo y, il valore resta praticamente costante. Ma appena ci si sposta di più riprende a variare.

    Domanda 4: le componenti del gradiente nel sistema x, y sono:

    \frac{\partial F}{\partial x}=-2x

    \frac{\partial F}{\partial y}=-2y

     

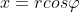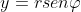    Domanda 5 (sapendo che x=rcos\varphi   e y=rsen\varphi):

    \frac{\partial F(r,\varphi )}{\partial r}=\frac{\partial F(x,y)}{\partial x}\cdot \frac{\partial x(r,\varphi )}{\partial r}+\frac{\partial F(x,y)}{\partial y}\cdot \frac{\partial y(r,\varphi )}{\partial r}=-2xcos\varphi -2ysen\varphi=-2rcos^{2}\varphi-2rsen^{2}\varphi=-2r(cos^{2}\varphi +sen^2\varphi )=-2r

     

    \frac{\partial F(r,\varphi )}{\partial \varphi }=\frac{\partial F(x,y)}{\partial x}\cdot \frac{\partial x(r,\varphi )}{\partial \varphi }+\frac{\partial F(x,y)}{\partial y}\cdot \frac{\partial y(r,\varphi )}{\partial \varphi }=2xrsen\varphi -2yrcos\varphi=2r^2sen\varphi cos\varphi -2r^2sen\varphi cos\varphi =0

     

     

     

     

  4. Fabrizio
    16/12/2020 at 10:14

    Arturo,

    non commento le tue risposte, ma avrai già confrontato i tuoi risultati con i miei.

    Sulla domanda 3: riesci anche a vedere dal grafico dove sono nulle le singole componenti?

    Rigurdo la tua osservazione "sarebbe ancora più evidente con una rappresentazione della funzione z=F(r, \varphi) nello spazio r, \varphi, z", ti do in parte ragione. D'altra parte una rappresentazione di questo tipo introduce una dimensione in più che non esiste nello spazio bidimensionale che stiamo considerando. Questo potrebbe essere fuorviante in alcuni casi perché credo ci allontani dal significato di quella funzione.  Peraltro questa dimensione in più possiamo aggiungerla solo nel caso di spazio bidimensionale, già con uno spazio 3D non è possibile e tantomeno con un 4D.

    Personalmente trovo più utile cercare di immaginare, finché riesco,  i campi dei valori di queste funzioni come qualcosa di inserito nello spazio come una densità o un colore.

  5. Arturo Lorenzo
    16/12/2020 at 14:55

    Sulla domanda 3: la singola componente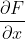 \frac{\partial F}{\partial x} del gradiente e' nulla lungo la retta x=0, cioe' lungo l'asse y. Idem per l'altra componente, nulla lungo l'asse x.

    Ok Fabrizio per il resto. Non ha caso avevo preposto alla mia osservazione un "Forse" :wink:

  6. Arturo Lorenzo
    16/12/2020 at 14:56

    (Non "a" caso, digitavo con lo smartphone)

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.